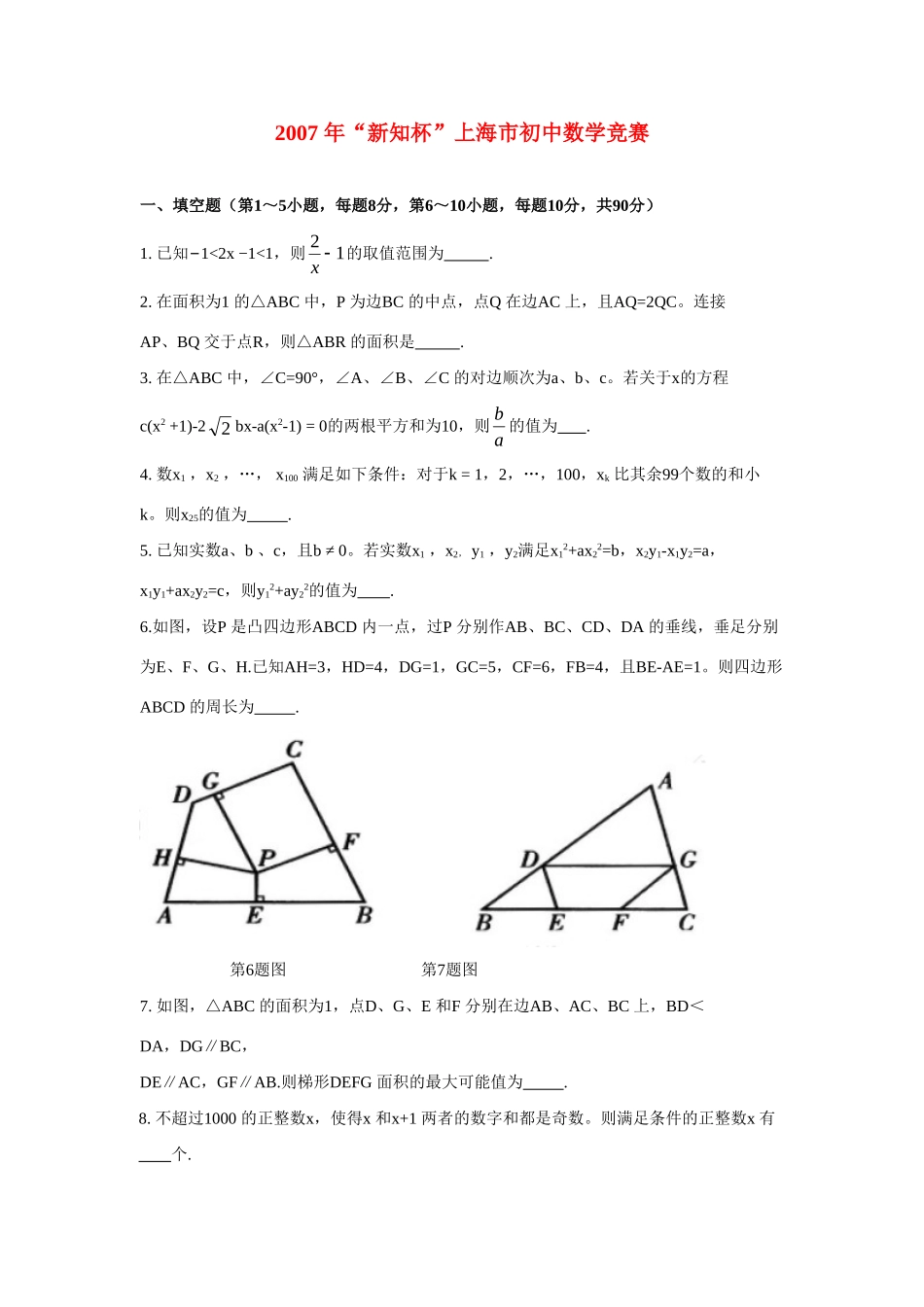
2007年“新知杯”上海市初中数学竞赛一、填空题(第1~5小题,每题8分,第6~10小题,每题10分,共90分)1.已知−1<2x−1<1,则12x的取值范围为.2.在面积为1的△ABC中,P为边BC的中点,点Q在边AC上,且AQ=2QC。连接AP、BQ交于点R,则△ABR的面积是.3.在△ABC中,∠C=90°,∠A、∠B、∠C的对边顺次为a、b、c。若关于x的方程c(x2+1)-22bx-a(x2-1)=0的两根平方和为10,则ab的值为.4.数x1,x2,…,x100满足如下条件:对于k=1,2,…,100,xk比其余99个数的和小k。则x25的值为.5.已知实数a、b、c,且b≠0。若实数x1,x2,y1,y2满足x12+ax22=b,x2y1-x1y2=a,x1y1+ax2y2=c,则y12+ay22的值为.6.如图,设P是凸四边形ABCD内一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1。则四边形ABCD的周长为.第6题图第7题图7.如图,△ABC的面积为1,点D、G、E和F分别在边AB、AC、BC上,BD<DA,DG∥BC,DE∥AC,GF∥AB.则梯形DEFG面积的最大可能值为.8.不超过1000的正整数x,使得x和x+1两者的数字和都是奇数。则满足条件的正整数x有个.9.已知k为不超过50的正整数,使得对任意正整数n,2×36n+k×23n+1-1都能被7整除。则这样的正整数k有个.10.使得22)1(pp是完全平方数的所有质数p为.二、(20分)如图,在Rt△ABC中,∠C=90°,BC=2,AC=x,点F在边AB上,点G、H在边BC上,四边形EFGH是一个边长为y的正方形,且AE=AC.(1)求y关于x的函数解析式.(2)当x为何值时,y取到最大值?并求出y的最大值.三、(20分)求满足下列条件的正整数n的所有可能值:对这样的n,能找到实数a、b,使得函数baxxnxf21)(对任意整数x,f(x)都是整数.四、(20分)在一个盒子里有红、黄、黑三种颜色的小球共88个.已知从中任意取出24个,就可以保证至少有10个小球是同色的.问在满足上述条件下,无论各种颜色的小球如何分配,至少要从盒子中任意取出多少个小球,才能保证至少有20个小球是同色的?