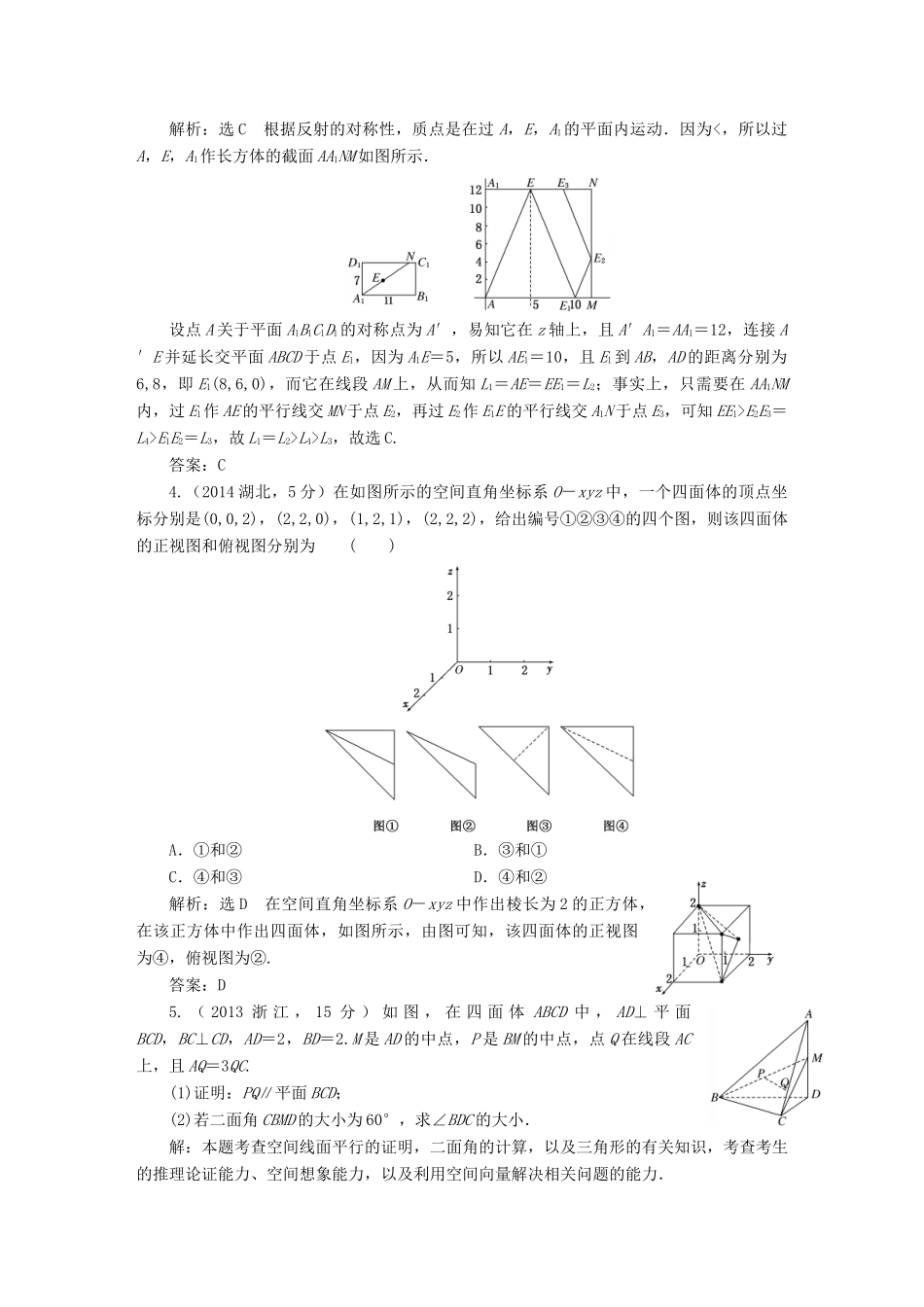
第七章立体几何第六节空间向量及其运算和空间位置关系1.(2014广东,5分).已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是()A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)解析:各选项给出的向量的模都是,|a|=.对于选项A,设b=(-1,1,0),则cos〈a,b〉===-,因为0°≤〈a,b〉≤180°,所以〈a,b〉=120°.对于选项B,设b=(1,-1,0),则cos〈a,b〉===.因为0°≤〈a,b〉<180°,所以〈a,b〉=60°,正确.对于选项C,设b=(0,-1,1),则cos〈a,b〉===-.因为0°≤〈a,b〉≤180°,所以〈a,b〉=120°.对于选项D,设b=(-1,0,1).则cos〈a,b〉===-1.因为0°≤〈a,b〉≤180°,所以〈a,b〉=180°,故选B.答案:B2.(2014北京,5分)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,).若S1,S2,S3分别是三棱锥D-ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则()A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S1解析:根据题目条件,在空间直角坐标系Oxyz中作出该三棱锥D-ABC,显然S1=S△ABC=×2×2=2,S2=S3=×2×=.故选D.答案:D3.(2014江西,5分)如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12).遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为Li(i=2,3,4),L1=AE,将线段L1,L2,L3,L4竖直放置在同一水平线上,则大致的图形是()解析:选C根据反射的对称性,质点是在过A,E,A1的平面内运动.因为<,所以过A,E,A1作长方体的截面AA1NM如图所示.设点A关于平面A1B1C1D1的对称点为A′,易知它在z轴上,且A′A1=AA1=12,连接A′E并延长交平面ABCD于点E1,因为A1E=5,所以AE1=10,且E1到AB,AD的距离分别为6,8,即E1(8,6,0),而它在线段AM上,从而知L1=AE=EE1=L2;事实上,只需要在AA1NM内,过E1作AE的平行线交MN于点E2,再过E2作E1E的平行线交A1N于点E3,可知EE1>E2E3=L4>E1E2=L3,故L1=L2>L4>L3,故选C.答案:C4.(2014湖北,5分)在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①②③④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C.④和③D.④和②解析:选D在空间直角坐标系O-xyz中作出棱长为2的正方体,在该正方体中作出四面体,如图所示,由图可知,该四面体的正视图为④,俯视图为②.答案:D5.(2013浙江,15分)如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.(1)证明:PQ∥平面BCD;(2)若二面角CBMD的大小为60°,求∠BDC的大小.解:本题考查空间线面平行的证明,二面角的计算,以及三角形的有关知识,考查考生的推理论证能力、空间想象能力,以及利用空间向量解决相关问题的能力.法一:(1)证明:取BD的中点O,在线段CD上取点F,使得DF=3FC,连接OP,OF,FQ.因为AQ=3QC,所以QF∥AD,且QF=AD.因为O,P分别为BD,BM的中点,所以OP是△BDM的中位线,所以OP∥DM,且OP=DM.又点M为AD的中点,所以OP∥AD,且OP=AD.从而OP∥FQ,且OP=FQ,所以四边形OPQF为平行四边形,故PQ∥OF.又PQ⊄平面BCD,OF⊂平面BCD,所以PQ∥平面BCD.(2)作CG⊥BD于点G,作GH⊥BM于点H,连接CH.因为AD⊥平面BCD,CG⊂平面BCD,所以AD⊥CG,又CG⊥BD,AD∩BD=D,故CG⊥平面ABD,又BM⊂平面ABD,所以CG⊥BM.又GH⊥BM,CG∩GH=G,故BM⊥平面CGH,∴BM⊥CH,所以∠CHG为二面角CBMD的平面角,即∠CHG=60°.设∠BDC=θ.在Rt△BCD中,CD=BDcosθ=2cosθ,CG=CDsinθ=2cosθsinθ,BC=BDsinθ=2sinθ,BG=BCsinθ=2sin2θ.在Rt△BDM中,HG==.在Rt△CHG中,tan∠CHG===.所以tanθ=.从而θ=60°,即∠BDC=60°.法二:(1)证明:如图,取BD的中点O,以O为原点,OD,OP所在射线为y,z轴的正半轴,建立空间直角坐标系Oxyz.由题意知A(0,,2),B(0,-,0),D(0,,0).设点C的坐标为(x0,y0,0).因为=3,所以Q.因为M为AD的中点,故M(0...