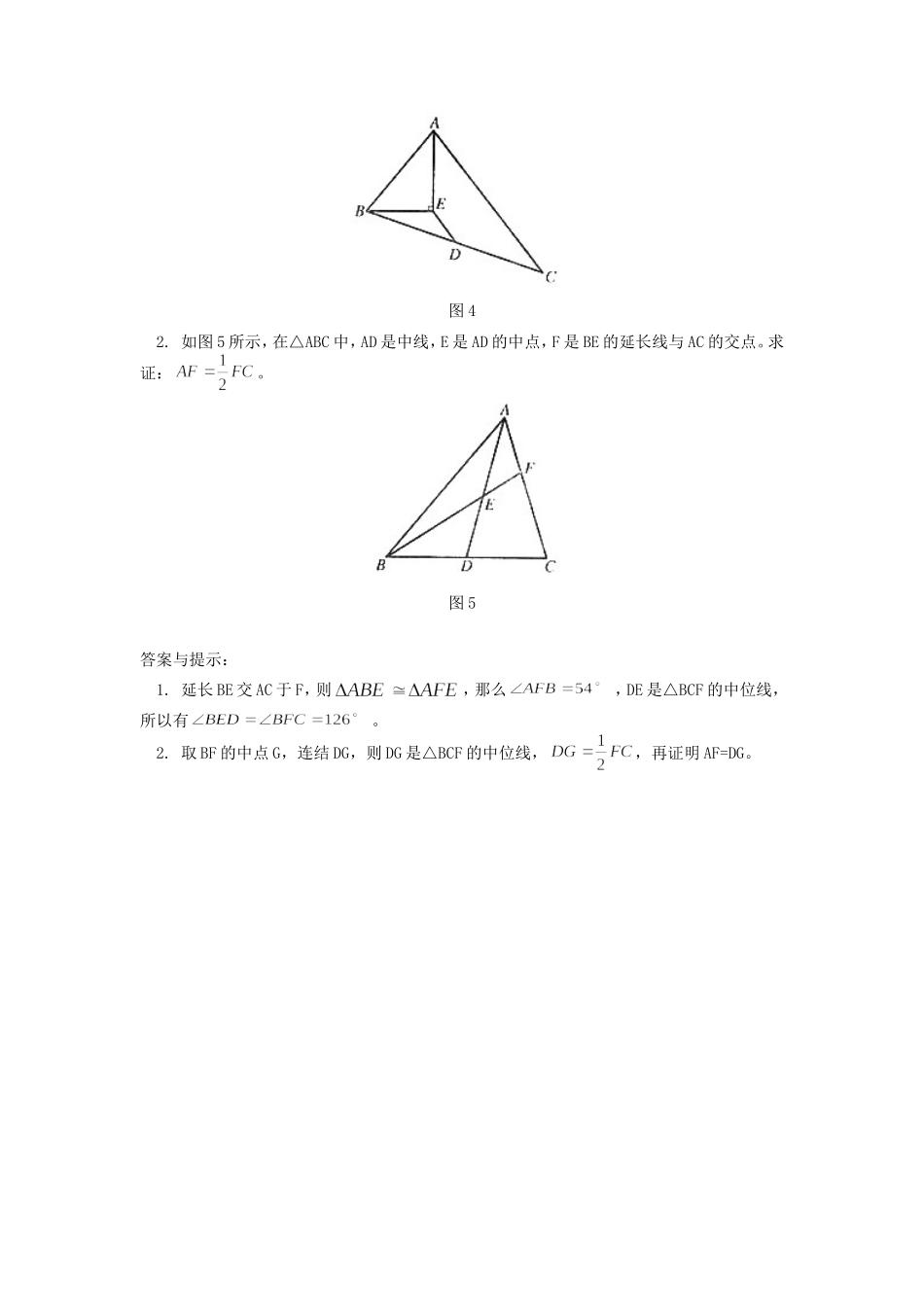
初中数学巧用三角形中位线的两种关系安义人学习了三角形的中位线定理后,我们不难发现,该定理其实包括如下两种关系:1.位置关系,即三角形的中位线平行于第三边;2.数量关系,即三角形的中位线等于第三边的一半。解答某些与线段中点有关的问题时,要注意灵活巧用这两种关系。例1.如图1所示,EF是△ABC的中位线,BD平分交EF于D,若ED=2,则EB=________________。图1解:在△ABC中,因为EF是△ABC的中位线所以EF//BC所以因为所以所以例2.如图2所示,在△ABC中,AC=5,中线AD=4,则AB边的取值范围是()A.B.C.D.图2解:取AB的中点E,连结DE因为所以DE是△ABC的中位线所以因为所以所以应选B。例3.如图3所示,四边形ABCD中,AC与BD相交于E,BD=AC,M,N分别是AD,BC的中点,MN分别交AC,BD于F,G,求证:EF=EG。图3证明:取AB的中点P,连结PM,PN因为M,P分别是AB,AD的中点所以PM是△ABD的中位线所以同理所以因为BD=AC所以所以所以练习:1.如图4所示,AE平分,垂足为E,D为BC的中点,,则BED=_____________。图42.如图5所示,在△ABC中,AD是中线,E是AD的中点,F是BE的延长线与AC的交点。求证:。图5答案与提示:1.延长BE交AC于F,则,那么,DE是△BCF的中位线,所以有。2.取BF的中点G,连结DG,则DG是△BCF的中位线,,再证明AF=DG。