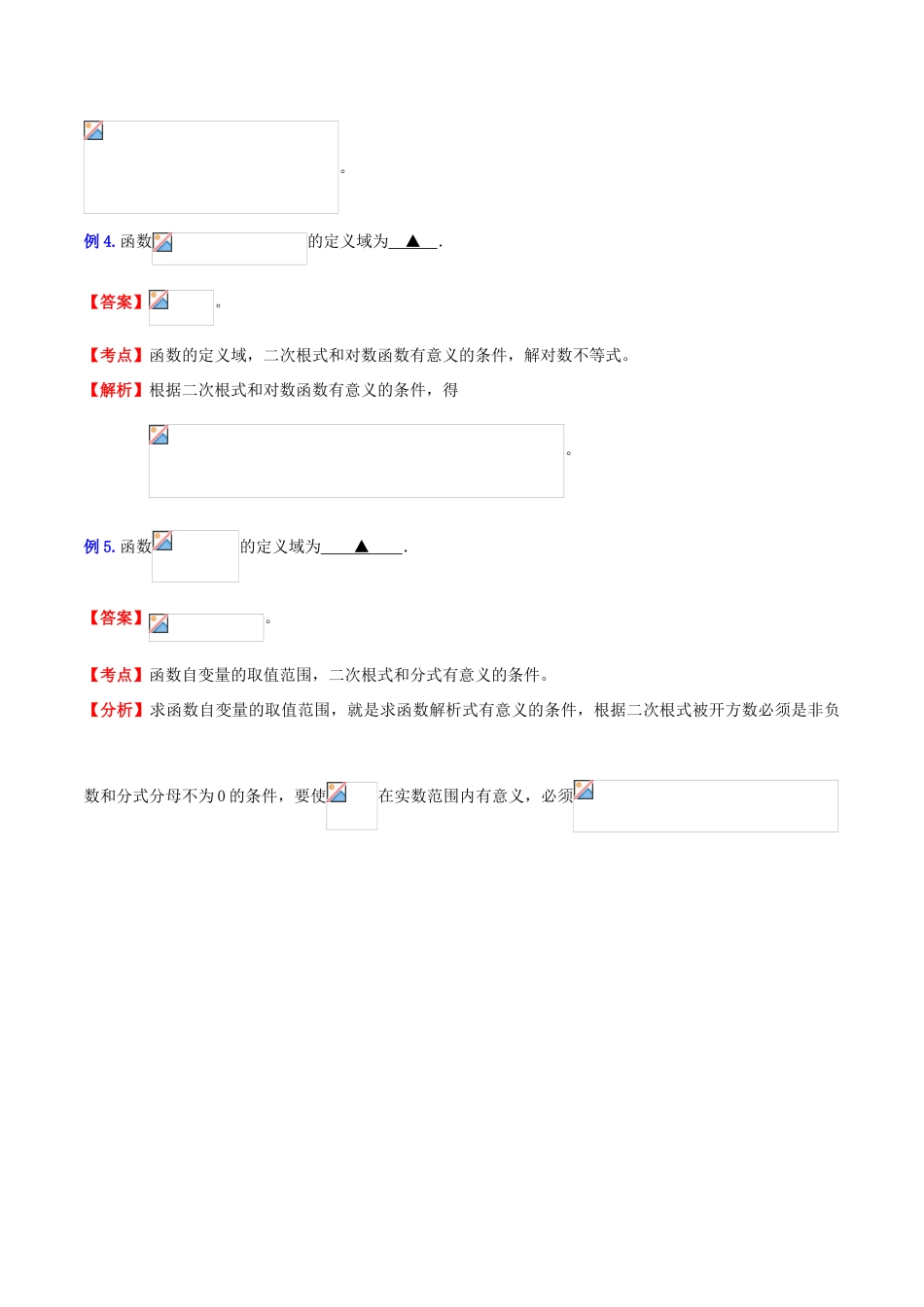
第16讲:高频考点分析之函数探讨1~2讲,我们对客观性试题解法进行了探讨,3~8讲,对数学思想方法进行了探讨,9~12讲对数学解题方法进行了探讨,从第13讲开始我们对高频考点进行探讨。函数问题是中学数学的重要内容,在高考中占有比较重要的地位。结合中学数学的知识,高考中函数问题主要有以下几种:1.函数定义域问题;2.函数值和大小比较问题;3.函数的值域和最值问题;4.函数的单调性。周期性、奇偶性问题;5.函数的零点问题;6.函数图象的交点问题;7.反函数问题;8.函数的图形问题;9.函数的综合问题我们从以上九方面探讨函数问题的求解。一、函数定义域问题:典型例题:例1.函数的定义域为【】ABCD【答案】B。【考点】函数的定义域。分式、对数、二次根式有意义的条件。【解析】根据分式、对数、二次根式有意义的条件,得,解得。∴函数的定义域为。故选B。例2.下列函数中,与函数定义域相同的函数为【】A.B.C.D.【答案】D。【考点】函数的定义域。【解析】求函数的定义域的依据就是要使函数的解析式有意义的自变量的取值范围。其求解根据一般有:(1)分式中,分母不为零;(2)偶次根式中,被开方数非负;(3)对数的真数大于0:(4)实际问题还需要考虑使题目本身有意义。由函数的意义可求得其定义域为,于是对各选项逐一判断即可得答案:对于A,的其定义域为,故A不满足;对于B,的定义域为,故B不满足;对于C,的定义域为,故C不满足;对于D,的定义域为,故D满足。综上所述,与函数定义域相同的函数为:。故选D。例3.函数的定义域是▲。(用区间表示)【答案】()【考点】函数自变量的取值范围,二次根式和分式有意义的条件。【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使在实数范围内有意义,必须。例4.函数的定义域为▲.【答案】。【考点】函数的定义域,二次根式和对数函数有意义的条件,解对数不等式。【解析】根据二次根式和对数函数有意义的条件,得。例5.函数的定义域为▲.【答案】。【考点】函数自变量的取值范围,二次根式和分式有意义的条件。【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使在实数范围内有意义,必须