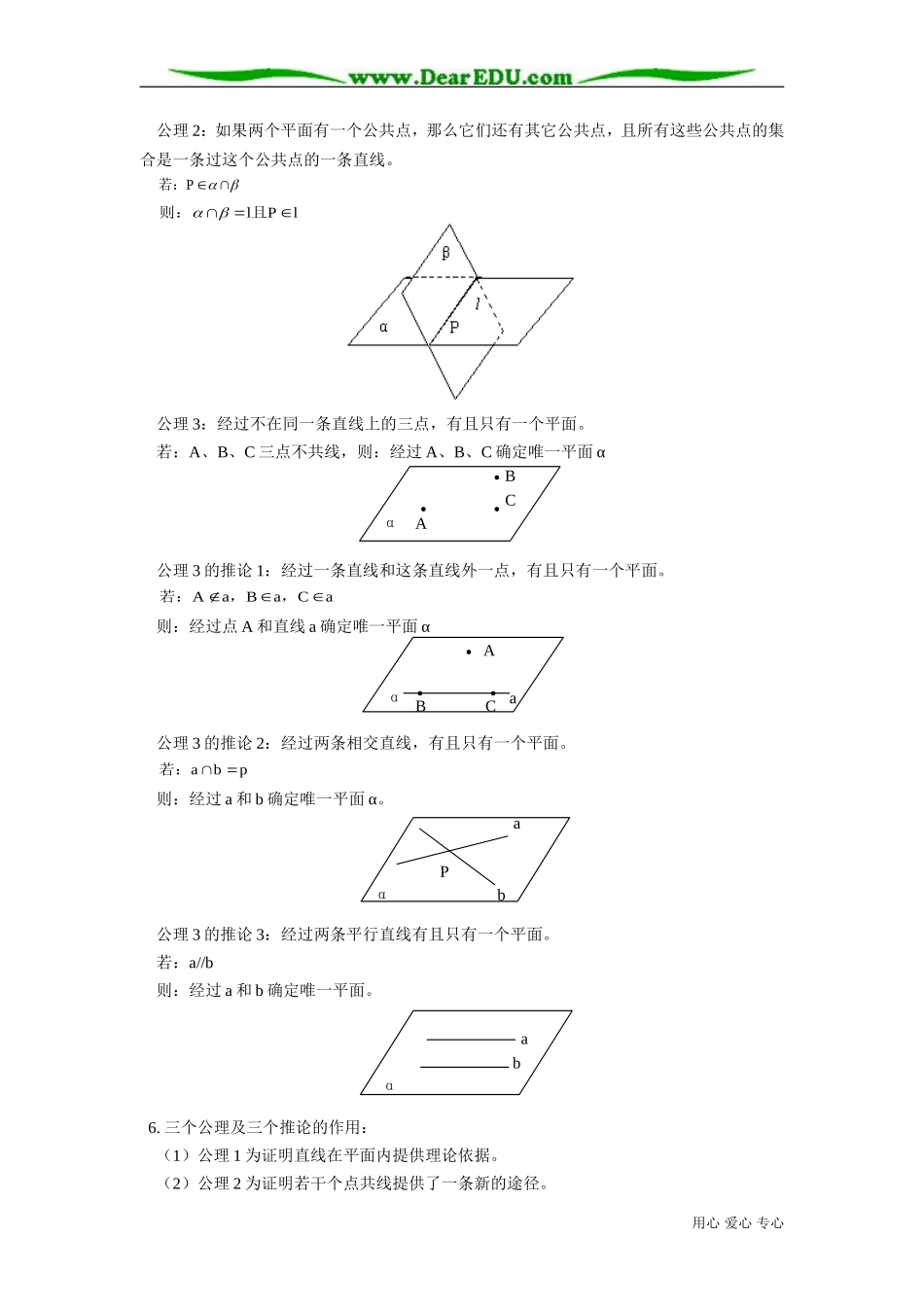
高二数学立体几何新课预习人教版一.本周教学内容:《立体几何新课预习》教学目标:1.理解平面的概念,掌握平面的画法和记法。掌握用符号表示点、线、面之间的关系。2.理解并掌握平面的基本性质。3.理解并掌握3个公理及推论证明三点共线和若干个点、线共面问题。能力目标:逐步培养学生的空间想象能力,在已有的平面图形知识的基础上,建立空间观念,实现从认识平面图形到认识立体图形这一飞跃。二.重点与难点:重点:掌握并熟记平面基本性质的3个公理及三个推论;难点:平面基本性质在证题中的应用。教学过程:一.平面的有关概念及符号表示:1.平面的概念:常见的桌面、黑板面、平静的水面等。都给我们以平面的形象,几何里的平面就是从这样的一些物体中抽象出来的,与之不同的是几何里的平面是可以无限延伸的。注:平面的概念是用描述性的语言进行说明的。2.平面的画法:基本规则:(1)通常画平行四边形表示平面。(2)当平面水平放置时,把平行四边形的锐角画成45°,横边画成邻边的2倍长。如图(A)DC45°AB图(A)(3)当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画。如图(B)用心爱心专心βBBααADA图(B)3.点、线、面的字母表示:(1)平面的表示方法:(i)可以用一个希腊字母:α、β、γ来表示。(ii)也可以用表示平面的平行四边形的顶点字母来表示。如:平面ABCD。(iii)也可以用表平行四边形的两个相对顶点字母来表示。如:平面AC,或平面BD。(2)直线的表示方法:(i)可以用两个大写字母表示直线,如:直线AB(ii)也可以用一个小写字母表示直线,如:直线,a、b、l等。(3)点的表示方法:一般都用一个大写字母表示点。如:点A、B、C等。4.用符号表示点、线、面之间的关系:说明:(1)平面内有无数个点,平面可以看成是由它内部的所有的点组成的点集。其中每个点都是它的元素;(2)直线上有无数个点,直线可以看成是由它上面的所有点组成的点集,其中每一个点都是它的一个元素。于是:(1)点A在平面α内,记作:A∈α(2)点A在直线l上,记作:A∈l()点不在直线上,记作3AlAl()直线在平面内,记作4ll()直线不在平面内,记作5ll5.平面的基本性质:公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内若:,,且,,则:AlBlAl.lAαB说明:以上用三种语言叙述了公理1,即:文字语言,图形语言和符号语言。这三种语言要能互译。用心爱心专心公理2:如果两个平面有一个公共点,那么它们还有其它公共点,且所有这些公共点的集合是一条过这个公共点的一条直线。若:P则:且lPl公理3:经过不在同一条直线上的三点,有且只有一个平面。若:A、B、C三点不共线,则:经过A、B、C确定唯一平面αBCαA公理3的推论1:经过一条直线和这条直线外一点,有且只有一个平面。若:,,AaBaCa则:经过点A和直线a确定唯一平面αAαaBC公理3的推论2:经过两条相交直线,有且只有一个平面。若:abp则:经过a和b确定唯一平面α。aPαb公理3的推论3:经过两条平行直线有且只有一个平面。若:a//b则:经过a和b确定唯一平面。abα6.三个公理及三个推论的作用:(1)公理1为证明直线在平面内提供理论依据。(2)公理2为证明若干个点共线提供了一条新的途径。用心爱心专心(3)公理3和它的三个推论为确定唯一平面提供依据。二.例题分析:例1:选择题:1.两个不重合的平面有公共点,则公共点的个数为()A.2个B.有无数个且在一条直线上C.一个或无数个D.1个2.点A在直线l上,l在平面α外,用符号表示正确的是()AAllBAll..,,CAllDAA..,,3.若,,,,则()abcabMAMcBMcCMDM....解1:根据公理2,应选(B)解2:主要考你符号表示,应视,直线和平面为点的集合,而点视为集合中的元素,再根据元素与集合,集合与集合之间的关系显然应选(B)解3:根据公理2及集合之间的关系应选(A)例2.直线AB、BC、CA两两相交,交点分别为A、B、C,判断这三条直线是否共面,并说明理由。解:这三条直线共面,理由...