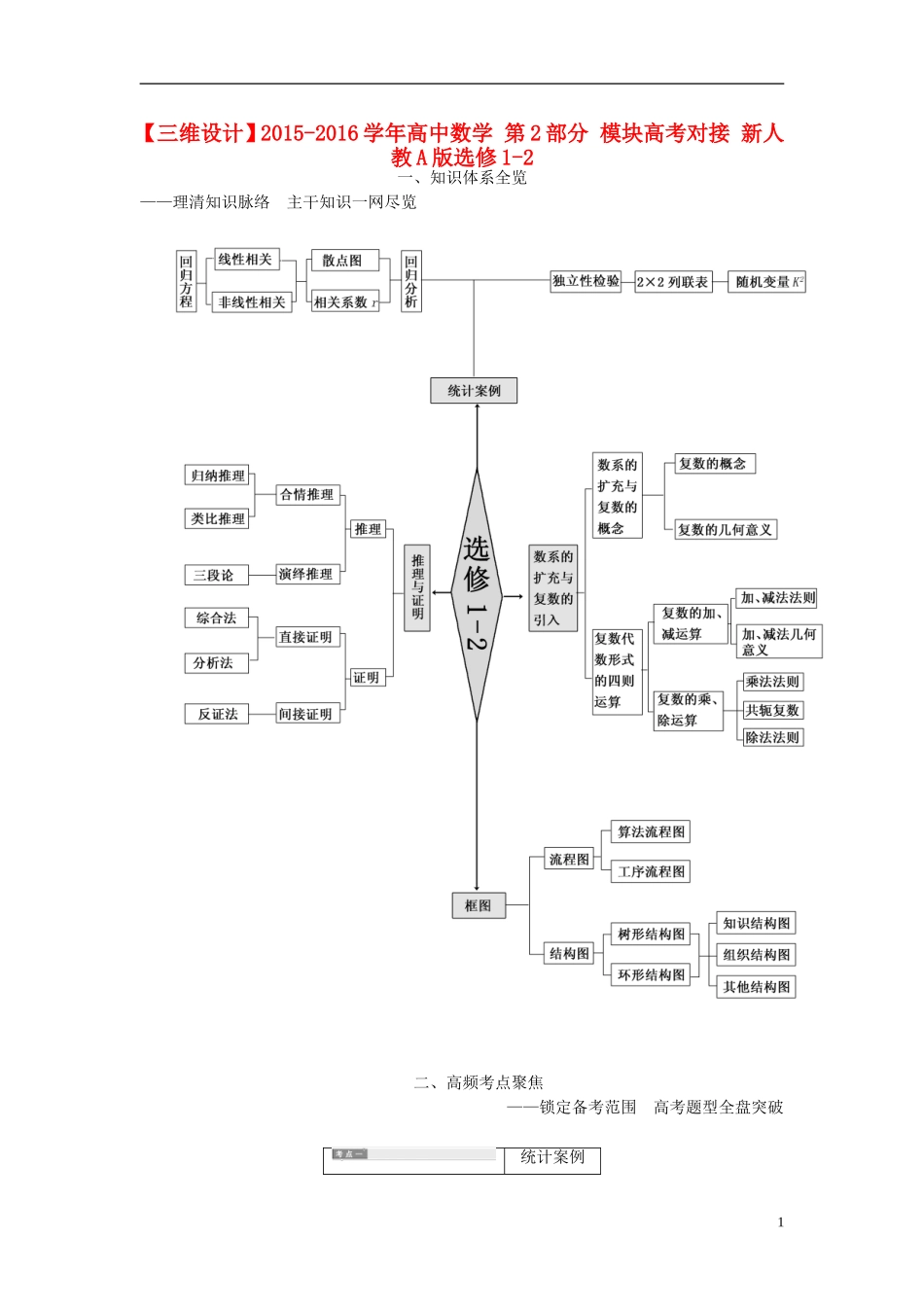
【三维设计】2015-2016学年高中数学第2部分模块高考对接新人教A版选修1-2一、知识体系全览——理清知识脉络主干知识一网尽览二、高频考点聚焦——锁定备考范围高考题型全盘突破统计案例11.题型既有选择、填空题,也有解答题.主要考查回归直线方程的求解与应用、独立性检验中K2与相关系数的求解与判断.2.对独立性检验问题要准确记忆K2公式中各字母的意义并准确计算.解决线性回归分析问题的关键是利用“一点一式”求方程,即利用数据的“中心点”和已知的公式.计算的准确性是解决此类问题最基本的要求.[例1](重庆高考)从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得∑xi=80,∑yi=20,∑xiyi=184,∑x=720.(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;(2)判断变量x与y之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.附:线性回归方程y=bx+a中,b=,a=y-bx,其中x,y为样本平均值,线性回归方程也可写为y=bx+a.[解](1)由题意知n=10,=∑xi==8,y=∑yi==2.又∑x-nx2=720-10×82=80,∑xiyi-nxy=184-10×8×2=24,由此可得b===0.3,a=y-bx=2-0.3×8=-0.4,故所求回归方程为y=0.3x-0.4.(2)由于变量y的值随x的值增加而增加(b=0.3>0),故x与y之间是正相关.(3)将x=7代入回归方程可以预测该家庭的月储蓄为y=0.3×7-0.4=1.7(千元).1.(福建高考)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到如图所示的频率分布直方图.(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?P(χ2≥k)0.1000.0500.0100.001k2.7063.8416.63510.828附:χ2=2解:(1)由已知得,样本中有25周岁以上组工人60名,25周岁以下组工人40名.所以,样本中日平均生产件数不足60件的工人中,25周岁以上组工人有60×0.05=3(人),记为A1,A2,A3;25周岁以下组工人有40×0.05=2(人),记为B1,B2.从中随机抽取2名工人,所有的可能结果共有10种,它们是:(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).其中,至少1名“25周岁以下组”工人的可能结果共有7种,它们是(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).故所求的概率P=.(2)由频率分布直方图可知,在抽取的100名工人中,“25周岁以上组”中的生产能手有60×0.25=15(人),“25周岁以下组”中的生产能手有40×0.375=15(人),据此可得2×2列联表如下:生产能手非生产能手合计25周岁以上组15456025周岁以下组152540合计3070100所以得χ2===≈1.79.因为1.79<2.706,所以没有90%的把握认为“生产能手与工人所在的年龄组有关”.合情推理与演绎推理1.题型多为选择题、填空题,主要考查归纳推理和类比推理,以及学生分析问题、解决问题的能力和逻辑推理能力.2.解决此类问题应重点关注以下两点:(1)要熟悉归纳推理、类比推理、演绎推理的一般原理、步骤、格式,搞清合情推理与演绎推理的联系与区别;(2)要把握归纳推理、类比推理、演绎推理的基本应用,在给定的条件下,能够运用归纳推理、类比推理获得新的一般结论,能够运用演绎推理对数学问题进行严格的证明.[例2](1)(陕西高考)观察下列等式12=112-22=-312-22+32=612-22+32-42=-10……照此规律,第n个等式可为________.(2)(湖北高考)古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1,3,6,10,…,第n个三角形数为=n2...