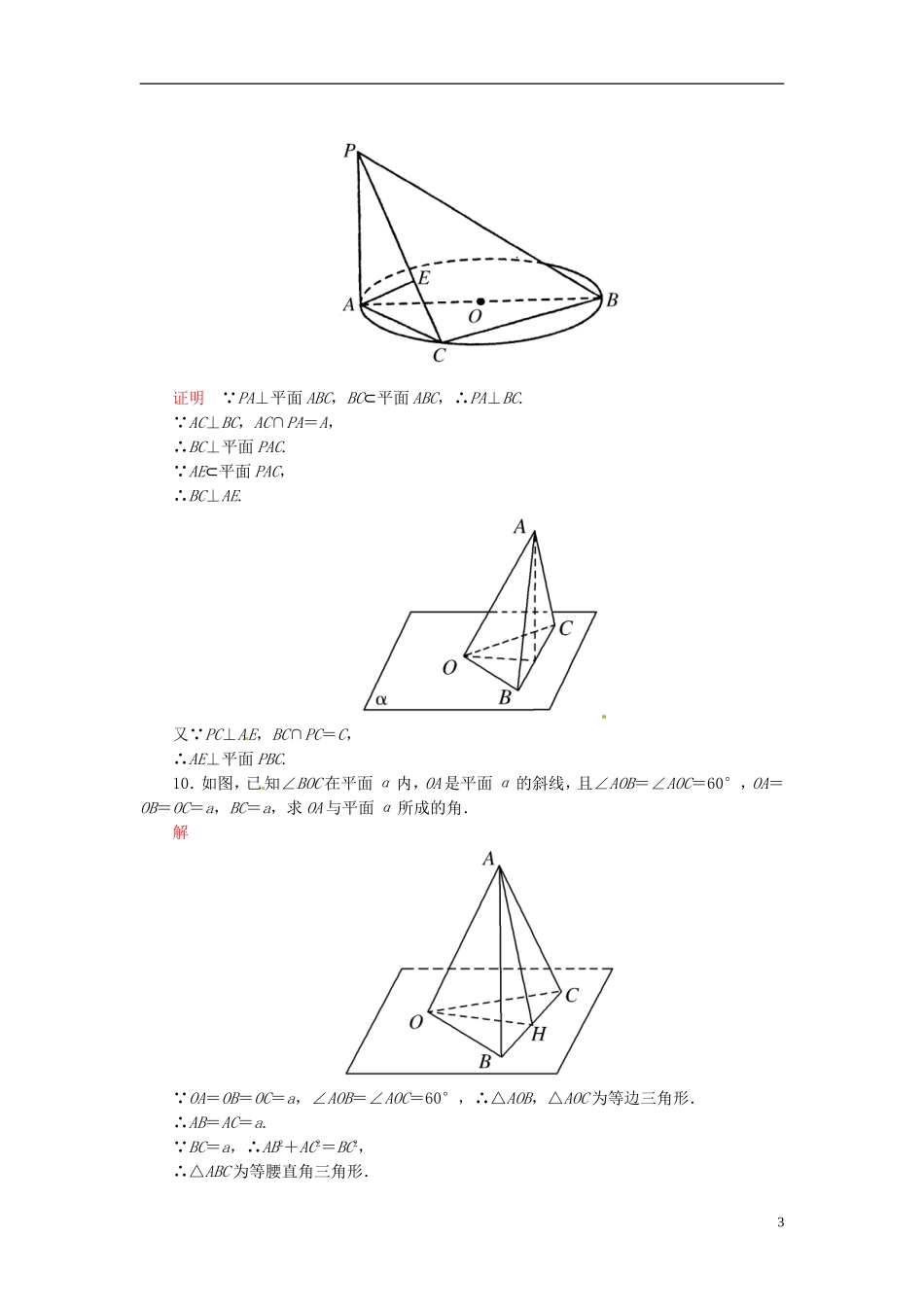
【名师一号】(学习方略)2015-2016学年高中数学2.3.1直线与平面垂直的判定双基限时练新人教A版必修21.垂直于梯形两腰的直线与梯形两底所在的平面的位置关系是()A.垂直B.平行C.a⊂αD.无法确定答案A2.已知直线a和两个平面α,β,给出下列四个命题:①若a∥α,则α内的任意直线都与a平行;②若a⊥α,则α内的任意直线都与a垂直;③若α∥β,则β内的任意直线都与α平行;④若a与α,β所成的角相等,则α∥β.则其中真命题为()A.①②B.②③C.①③D.③④解析由直线与平面垂直的定义知,若a⊥α,则α内的任意直线都与a垂直,所以②为真;若α∥β,则β内任意直线与α没有公共点,所以平行,故③为真.答案B3.空间四边形ABCD的四边相等,则它们的对角线AC,BD的关系是()A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交解析如图所示,ABCD是空间四边形.且AB=BC=CD=DA.取BD的中点E,连接AE,CE则有AE⊥BD,CE⊥BD.∴BD⊥平面ACE,∴BD⊥AC.∴空间四边形ABCD的对角线AC、BD垂直,但不相交.答案C4.a,b是直线,α是平面,下列判断正确的是()A.a垂直α内的两条直线,则a⊥αB.a⊥b,b⊥α,则a∥αC.a∥α,b⊥α,则a⊥bD.若a∥α,a∥β则α∥β解析用排除法,在A中,当两直线平行时,不成立;在B中,a可能在α内;在D中,α与β也可能相交.因此A、B、D均错,故C正确.答案C5.判断题:正确的在括号内打“√”号,不正确的打“×”号.1(1)如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直()(2)垂直于三角形两边的直线必垂直于第三边()(3)过点A垂直于直线a的所有直线都在过点A垂直于a的平面内()(4)如果三条共点直线两两垂直,那么其中一条直线垂直于另两条确定的平面()(5)已知a∥α,且b⊥α,则b⊥a()(6)a∥b,a⊥β,则b⊥β()答案(1)×(2)√(3)√(4)√(5)√(6)√6.设O为平行四边形ABCD对角线的交点,P为平面AC外一点,且有PA=PC,PB=PD,则PO与平面ABCD的关系是__________.解析∵PA=PC,∴PO⊥AC,又PB=PD,∴PO⊥BD.∴PO⊥平面ABCD.答案垂直7.AB为⊙O的直径,C是异于A,B的圆周上的任意一点,PA垂直⊙O所在的平面,则△PAB,△PAC,△ABC,△PBC中共有________个直角三角形.答案48.如图,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,PA=AB,则直线PB与平面ABC所成的角是________.解析由PA⊥平面ABC知,∠PBA就是PB与平面ABC所成的角,在Rt△PAB中,由PA=AB,知∠PBA=45°.答案45°9.如图,已知PA⊥⊙O所在平面,AB为⊙O的直径,C是圆周上的任意一点,过A作AE⊥PC于E,求证:AE⊥平面PBC.2证明∵PA⊥平面ABC,BC⊂平面ABC,∴PA⊥BC.∵AC⊥BC,AC∩PA=A,∴BC⊥平面PAC.∵AE⊂平面PAC,∴BC⊥AE.又∵PC⊥AE,BC∩PC=C,∴AE⊥平面PBC.10.如图,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=a,求OA与平面α所成的角.解∵OA=OB=OC=a,∠AOB=∠AOC=60°,∴△AOB,△AOC为等边三角形.∴AB=AC=a.∵BC=a,∴AB2+AC2=BC2,∴△ABC为等腰直角三角形.3同理,△BOC也为等腰直角三角形.取BC的中点H,连接AH,OH,则AH=OH=a.∴AH2+OH2=OA2,∴△AOH为等腰直角三角形.∴∠AOH=45°,AH⊥OH.又AH⊥BC,∴AH⊥α.∴OA与平面α所成的角为45°.11.如图,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2.(1)证明PA∥平面BDE;(2)证明AC⊥平面PDB;(3)求直线BC与平面PDB所成的角的正切值.解(1)证明:连接AC,设AC∩BD=H,连接EH.在△ADC中,因为AD=CD,且DB平分∠ADC,所以H为AC的中点.又由题设E为PC的中点,故EH∥PA.又EH⊂平面BDE且PA⊄平面BDE,所以PA∥平面BDE.(2)证明:因为PD⊥平面ABCD,AC⊂平面ABCD,所以PD⊥AC.由(1)可得,DB⊥AC.又PD∩DB=D,故AC⊥平面PBD.(3)由AC⊥平面PBD,可知,BH为BC在平面PBD内的射影,所以∠CBH为直线BC与平面PBD所成的角.由AD⊥CD,AD=CD=1,DB=2,可得DH=CH=,BH=.在Rt△BHC中,tan∠CBH==.4所以直线BC与平面PBD所成的角的正切值为.5