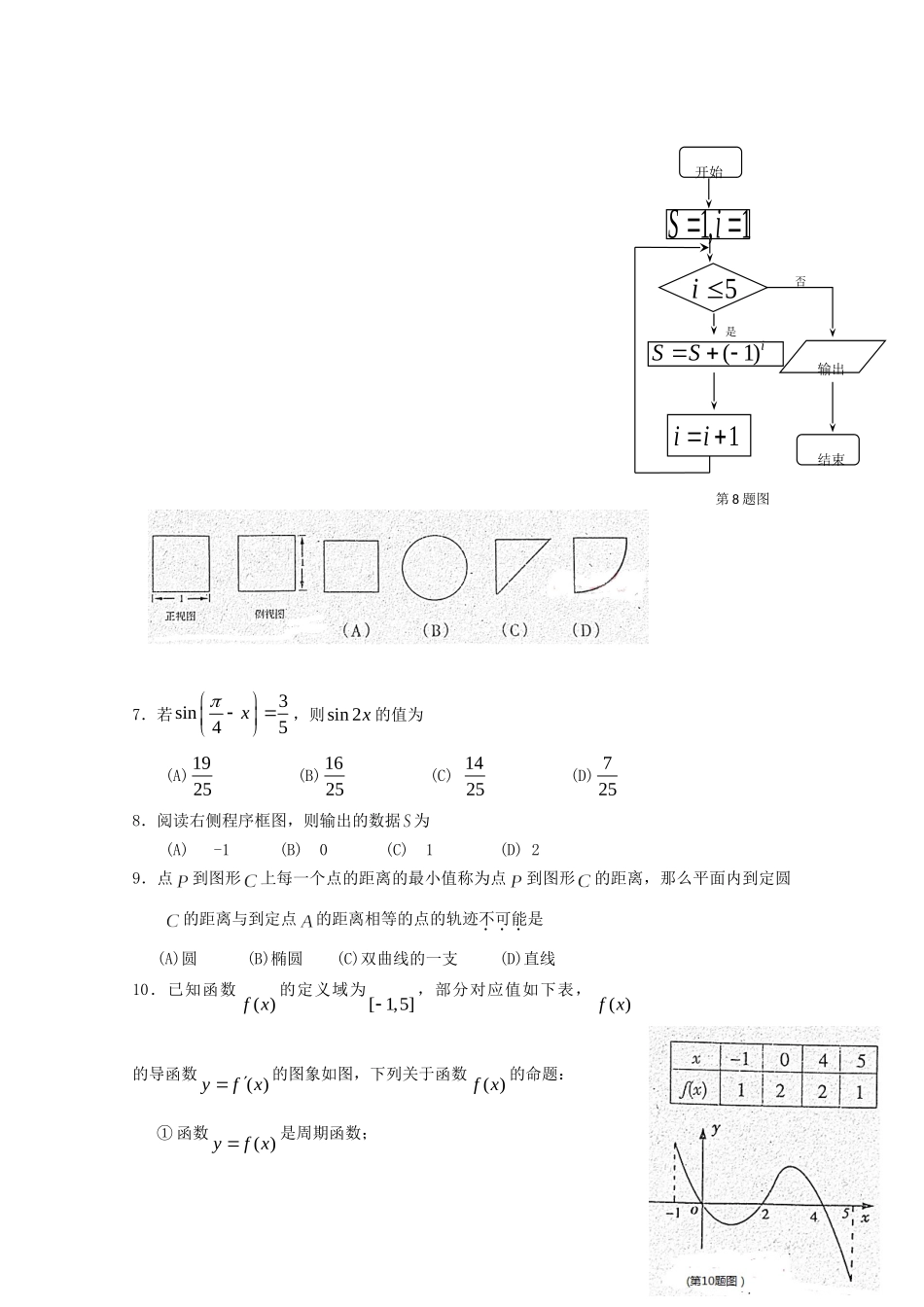
2012年泗县一中最后一卷数学(理)能力测试试题考试时间:120分钟试卷分值:150分第Ⅰ卷(共50分)一.选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一个是符合题目要求的。1.定义运算,则符合条件的复数的虚部为(A)(B)(C)(D)2.设213Axx,0Bxxa,若AB,则实数a的取值范围是(A)(),-1(B)(1],(C)(2),(D)(2],3.设是两个不同的平面,是一条直线,以下命题正确的是(A)若,则(B)若∥,∥,则(C)若∥,则(D)若∥,,则4.设函数为定义在R上的奇函数,当0x时,()22xfxxb(b为常数),则(1)f(A)52(B)1(C)3(D)35.二项式61(2)xx的展开式中的常数项为(A)120(B)120(C)160(D)1606.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积是12,则该几何体的俯视图可以是7.若3sin45x,则sin2x的值为(A)1925(B)1625(C)1425(D)7258.阅读右侧程序框图,则输出的数据为(A)-1(B)0(C)1(D)29.点到图形上每一个点的距离的最小值称为点到图形的距离,那么平面内到定圆的距离与到定点的距离相等的点的轨迹不可能是(A)圆(B)椭圆(C)双曲线的一支(D)直线10.已知函数()fx的定义域为[1,5],部分对应值如下表,()fx的导函数()yfx的图象如图,下列关于函数()fx的命题:①函数()yfx是周期函数;开始5i1,1iS1ii(1)iSS输出结束第8题图是否②函数()fx在[0,2]上是减函数;③如果当[1,]xt时,()fx的最大值是2,那么t的最大值为4;④当12a时,函数()yfxa有4个零点.其中真命题的个数是(A)4个(B)3个(C)2个(D)1个第Ⅱ卷(共100分)二.填空题:本大题共5小题,每小题5分,共25分。11.以直角坐标系的原点为极点,轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。直角坐标系中A点坐标为(-1,0),则A点极坐标为__________.12.为了了解某校今年准备报考飞行员的学生的体重情况,将样本数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的学生人数是__________.13.设变量,满足约束条件,则目标函数的最大值为.14.给出下列四个结论:①“若,则”的逆命题是真命题;②设,xyR,则“2x或2y”是“224xy”的充分不必要条件;③函数log(1)1(01)ayxaa且的图象必过点(0,1);④已知服从正态分布2(0)N,,且(20)0.4P,则(2)0.2P.其中正确结论的序号是_____________.(填上所有正确结论的序号)15.某校安排6个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有种。(用数字作答)三、解答题16、(本小题满分12分)在中,角所对的边分别是.已知,且.(1)求角的大小;(2)设且的最小正周期是,求在上的最大值.17、(本小题满分12分)当前人们普遍认为拓展训练是一种挑战极限、完善人格的训练,某大学生拓展训练中心着眼于大学生的实际情况,精心地设计了三个相互独立的挑战极限项目,并设置了如下计分办法:项目甲乙丙挑战成功得分103060挑战失败得分000据调查,大学生挑战甲项目的成功概率为,挑战乙项目的成功概率为,挑战丙项目的成功概率为.(1)求某同学三个项目至少一项挑战成功的概率;(2)记该同学挑战三个项目后所得分数为,求的分布列并预测该同学所得分数的数学期望.18、(本小题满分12分)如图所示,多面体中,是直角梯形,,平面,正平面,,为中点.(1)求证:平面;FABCEHD(2)求二面角的平面角的余弦值.19、(本小题满分13分)已知数列满足.(1)证明{}为等比数列,并求出通项公式;(2)设,的前项和为,证明:.20、(本小题满分13分)如图,为椭圆上的一个动点,弦分过别焦点,当轴时,恰好有(1)求椭圆的离心率;(2)设,试判断是否为定值?若是,求出该定值,若不是,请说明理由.21、(本小题满分13分)已知函数(1)当时,讨论的单调性;(2)设,若对,有,求的取值范围.xyA1F2FOBC