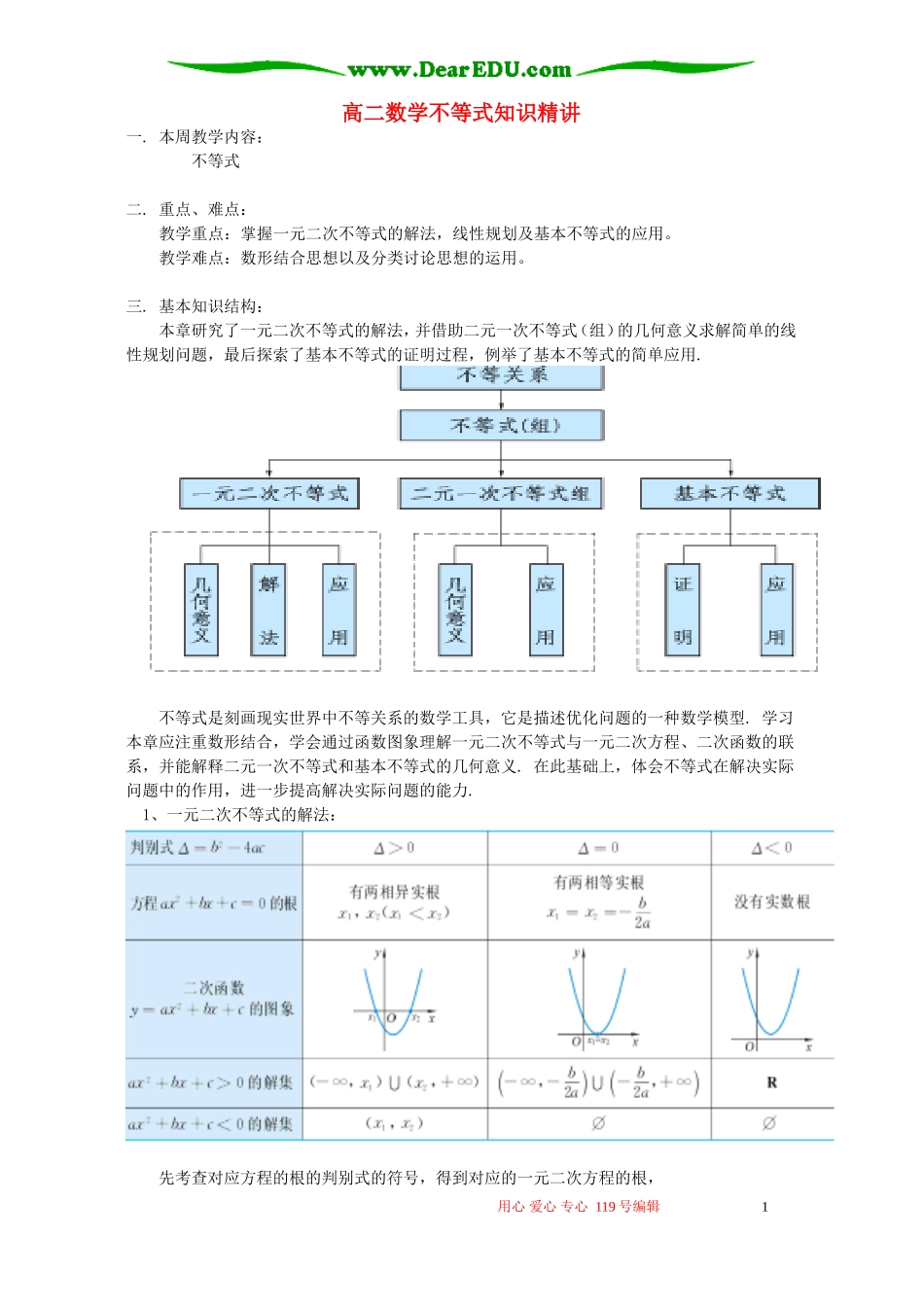
高二数学不等式知识精讲一.本周教学内容:不等式二.重点、难点:教学重点:掌握一元二次不等式的解法,线性规划及基本不等式的应用。教学难点:数形结合思想以及分类讨论思想的运用。三.基本知识结构:本章研究了一元二次不等式的解法,并借助二元一次不等式(组)的几何意义求解简单的线性规划问题,最后探索了基本不等式的证明过程,例举了基本不等式的简单应用.不等式是刻画现实世界中不等关系的数学工具,它是描述优化问题的一种数学模型.学习本章应注重数形结合,学会通过函数图象理解一元二次不等式与一元二次方程、二次函数的联系,并能解释二元一次不等式和基本不等式的几何意义.在此基础上,体会不等式在解决实际问题中的作用,进一步提高解决实际问题的能力.1、一元二次不等式的解法:先考查对应方程的根的判别式的符号,得到对应的一元二次方程的根,用心爱心专心119号编辑1考查对应的二次函数的图象根据图象写出对应的一元二次不等式的解集。2、二元一次不等式表示平面区域已知直线l:Ax+By+C=0①当B>0时,Ax+By+C>0表示直线l上方的平面区域;Ax+By+C<0表示直线l下方的平面区域②当B<0时,Ax+By+C>0表示直线l下方的平面区域;Ax+By+C<0表示直线l上方的平面区域;③当B=0时,(此时l⊥x轴)A>0Ax+By+C>0表示直线l右侧的平面区域;Ax+By+C<0表示直线l左侧的平面区域A<0时,仿A>0自行讨论。以上结论请自行证明。3、线性规划中的几个概念(1)不等式组①是一组对变量x、y的约束条件。(2)函数z=2x+y为目标函数。(3)满足线性约束条件的解(x、y)叫做可行解。(4)所有可行解组成的集合叫做可行域。(5)使线性目标函数取得最大或最小值的可行解叫做最优解。4、掌握比较大小的常用方法:①基本结论:利用常见的基本不等式,直接比较两个代数式的大小。这里主要是利用:当a、b∈R+时,≤≤及其变形公式②作差、作商、平方作差法,根据题目的特点,合理选用。这在证明题中要比较两个代数式的大小时经常使用。5、熟练掌握用均值不等式求最值,必须注意三个条件:一正;二定;三相等。三者缺一不可。如不满足条件时求最值可以结合函数的单调性来解决。如求函数(x≥1)的最小值。6、不等式证明的常规方法有:比较法、综合法、分析法。7、把握解含参数的不等式的注意事项解含参数的不等式时,首先应注意考查是否需要进行分类讨论.如果遇到下述情况则一般需要讨论:①不等式两端乘除一个含参数的式子时,则需讨论这个式子的正、负、零性.②在求解过程中,需要使用指数函数、对数函数的单调性时,则需对它们的底数进行讨论.③在解含有字母的一元二次不等式时,需要考虑相应的二次函数的开口方向,对应的一元二次方程根的状况(有时要分析△),比较两个根的大小。【例1】解不等式:x2-(a+a2)x+a3<0。解题思路分析:因x2-(a2+a)x+a3=(x-a)(x-a2),不等式解的一般形式为两根a与a2之间,下面比较a与a2大小。用心爱心专心119号编辑2a-a2=a(1-a)当a=0或a=1时,a=a2,原不等式为x2<0,或(x-1)2<0,不等式无解当0
0,a>a2,不等式解为a21或a<0时,a(1-a)<0,a1,或a<0时,不等式的解为a0。解题思路分析:首先对二次项系数a讨论,以确定不等式的类型:当a=0时,原不等式为4x+4>0,x>-1。当a≠0时,不等式为二次不等式,其解的情况应考虑判别式△=16-16a=16(1-a)及二次项系数a的符号这两个因素,也就是讨论的标准为a与1与0的大小比较。当a>1时,不等式可化为△’=,不等式的解为R当00,解的形式为两根之外,求得方程两根为,,不等式的解为,或。当a<0时,不等式可化为,△’>0,解的形式为两根之间,不等式的解为,注意此时两根大小已改变。当a=1时,原不等式可化为x2+4x+4>0,(x+2)2>0∴x≠-2解:当a=0时,4x+4>0,x>-1,为原不等式的解当01时...