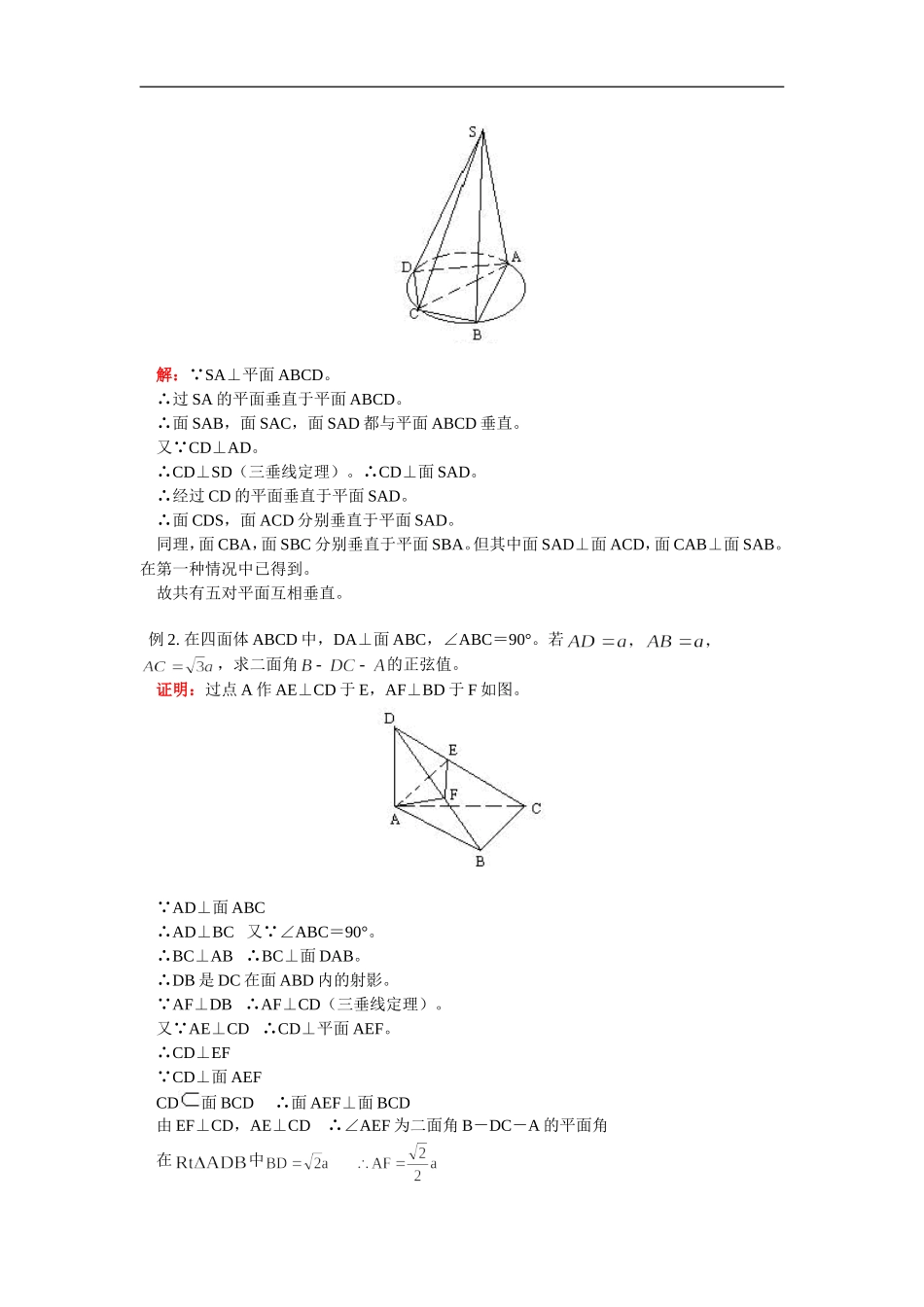
高二数学二面角、两平面垂直的判定和性质人教版【同步教育信息】一.本周教学内容:二面角、两平面垂直的判定和性质二.重点、难点:重点:1.二面角的有关概念:从一条直线出发的两个半平面所组成的图形叫二面角,这条直线叫二面角的棱。二面角的平面角的定义:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角。平面角是直角的二面角叫直二面角。2.作二面角的平面角常有以下方法:①若构成二面角的两个面有特殊性(如等腰三角形或直角三角形),可根据特殊图形的性质作出平面角。②若已知二面角内一点到两面的垂线,过两垂线作平面与两个面的交线所成的角就是二面角的平面角,称为垂面法。③若已知二面角一面内一点到另一面的垂线,用三垂线定理或它的逆定理作出平面角,称为三垂线法。④由定义找到棱上有关点,分别在两个面内作出(或找出)垂直于棱的射线,得到二面角的平面角。⑤当直观图上只给出两个平面的一个交点而没给出交线时,要先延展平面找到棱,用上述方法之一作出平面角。3.两个平面垂直的定义:两个平面相交,所成二面角是直二面角。作用:①用于证明两个平面垂直,证明二面角的平面角是直角。②两平面垂直,二面角为直二面角,平面角的二直线互相垂直。4.(1)两个平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。两个平面垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出垂直于一个平面的另一个平面的依据。由判定定理的内容可知,证明面面垂直,可以转化为证线面垂直。(2)性质定理如果两个平面垂直,那么一个平面内的垂直于它们的交线的直线垂直于另一个平面。简言为:“面面垂直,则线面垂直”。难点:1.二面角平面角的作法与计算。2.判定定理和性质定理的应用。【典型例题】例1.如图。AC为圆O的直径,B,D为圆上在AC两侧的两个点,SA⊥平面ABCD,连SB,SC,SD,试写出图中所有互相垂直的各对平面并说明理由。解: SA⊥平面ABCD。∴过SA的平面垂直于平面ABCD。∴面SAB,面SAC,面SAD都与平面ABCD垂直。又 CD⊥AD。∴CD⊥SD(三垂线定理)。∴CD⊥面SAD。∴经过CD的平面垂直于平面SAD。∴面CDS,面ACD分别垂直于平面SAD。同理,面CBA,面SBC分别垂直于平面SBA。但其中面SAD⊥面ACD,面CAB⊥面SAB。在第一种情况中已得到。故共有五对平面互相垂直。例2.在四面体ABCD中,DA⊥面ABC,∠ABC=90°。若,求二面角的正弦值。证明:过点A作AE⊥CD于E,AF⊥BD于F如图。 AD⊥面ABC∴AD⊥BC又 ∠ABC=90°。∴BC⊥AB∴BC⊥面DAB。∴DB是DC在面ABD内的射影。 AF⊥DB∴AF⊥CD(三垂线定理)。又 AE⊥CD∴CD⊥平面AEF。∴CD⊥EF CD⊥面AEFCD面BCD∴面AEF⊥面BCD由EF⊥CD,AE⊥CD∴∠AEF为二面角B-DC-A的平面角在中在又 AF⊥DB,AF⊥CD,BD∩CD=D∴AF⊥平面DBC,例3.在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求点P到直线a的距离。分析:设PA、PB分别为点P到平面M、N的距离,过PA、PB作平面α,分别交M、N于AQ、BQ。同理,有PB⊥a, PA∩PB=P,∴a垂直于面PAQB于Q又AQ、BQ平面PAQB∴AQ⊥a,BQ⊥a。∴∠AQB是二面角M-a-N的平面角。∴∠AQB=60°连PQ,则PQ是P到a的距离,在平面图形PAQB中,有∠PAQ=∠PBQ=90°∴P、A、Q、B四点共圆,且PQ是四边形PAQB的外接圆的直径2R在△PAB中, PA=1,PB=2,∠BPA=180°-60°=120°,由余弦定理得AB2=1+4-2×1×2cos120°=7由正弦定理:评注:本例题中,通过作二面角的棱的垂面,找到二面角的平面角。例4.在正方体ABCD-A1B1C1D1中,M是棱AA1的中点。求截面MB1D与底面ABCD所成二面角的大小。分析:如图。面MB1D与面ABCD只相交于点D,因此,要求二面角的大小,需先找或作出它的棱。由公理2及二面角棱的定义知,这条棱必过点D。只要再找出两个面的另一个交点即可。解: M是A1A的中点,∴MAB1B是直角梯形。延长其腰B1M与BA必相交于一点N。 MB1面B1DM,N∈MB1。∴N∈面B1DM。同理:N∈面ABCD。连结ND即为二面角的棱。连结DB, NA=BA=AD,∴∠ADB=∠ADN=45°。∴∠BDN=90°。...