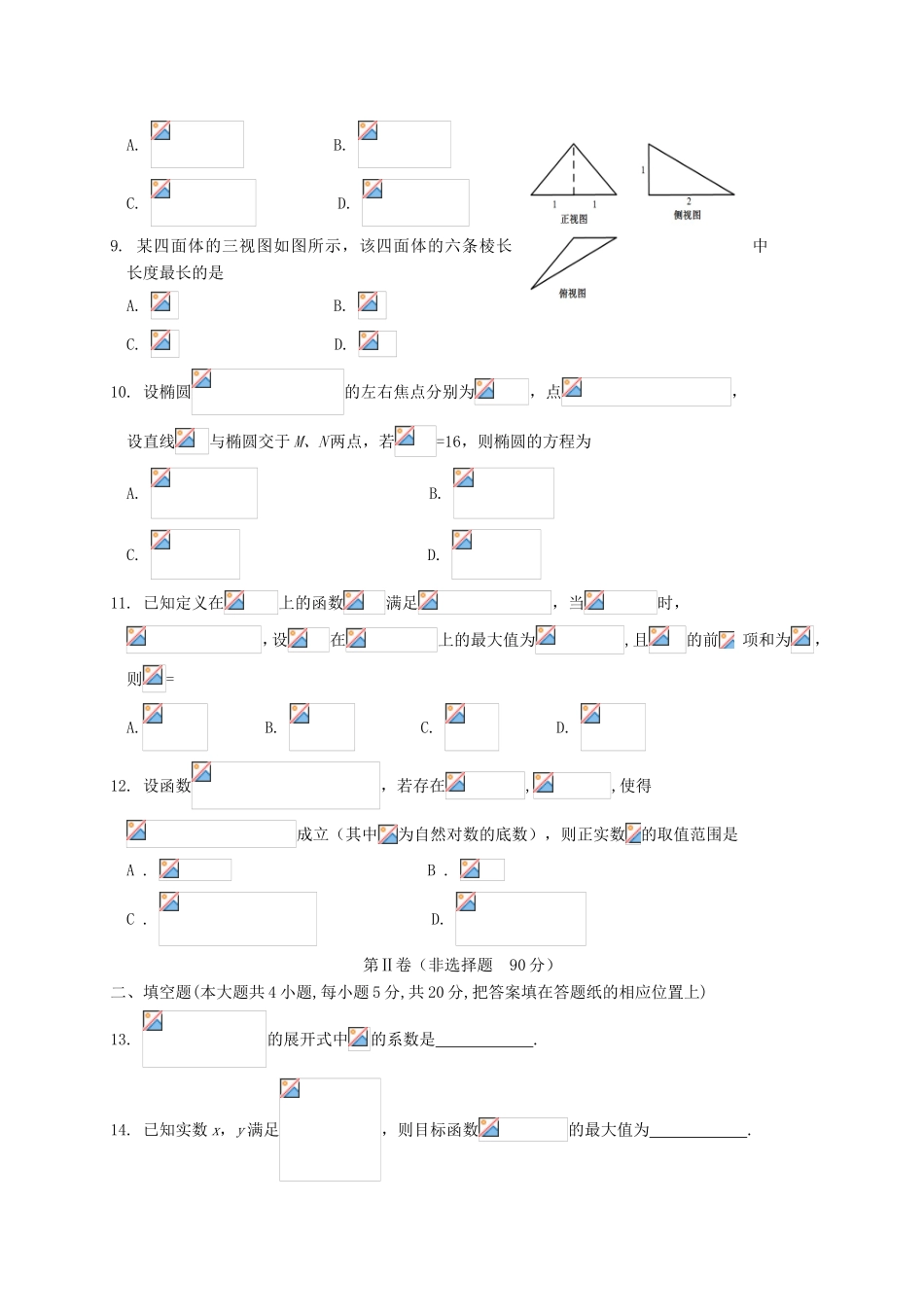
2015届高考考前仿真训练(一)数学试题(理)(满分150分,考试时间120分)第Ⅰ卷(选择题60分)一、选择题(5×12=60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项用2B铅笔涂黑答题纸上对应题目的答案标号)1.设全集集合,,则A.B.C.D.2.复数为纯虚数,若(为虚数单位),则实数的值为A.B.C.D.33.已知双曲线过点,则该双曲线的渐近线方程为A.B.C.D.4.执行如图所示的算法,则输出的结果是A.4B.3C.2D.15.把函数的图象向左平移个单位,得到函数的图象,若的图象关于对称,则A.B.C.D.6.从4名男生和6名女生中各选2人参加跳绳比赛,则男生甲和女生乙至少有一个被选中的概率是A.B.C.D.7.在三棱锥中,是边长为的正三角形,面,,则三棱锥外接球的表面积为A.B.C.D.8.已知,,则有A.B.C.D.9.某四面体的三视图如图所示,该四面体的六条棱长中长度最长的是A.B.C.D.10.设椭圆的左右焦点分别为,点,设直线与椭圆交于M、N两点,若=16,则椭圆的方程为A.B.C.D.11.已知定义在上的函数满足,当时,,设在上的最大值为,且的前项和为,则=A.B.C.D.12.设函数,若存在,,使得成立(其中为自然对数的底数),则正实数的取值范围是A.B.C.D.第Ⅱ卷(非选择题90分)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的相应位置上)13.的展开式中的系数是.14.已知实数x,y满足,则目标函数的最大值为.15.已知M为线段BC上一点,且,则的最大值为.16.在中,角的对边分别为,,则的最小值为.三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤,并把解答写在答卷纸的相应位置上)17.(本题满分12分)已知等差数列的公差,;等比数列满足:,,(1)求数列和的通项公式;(2)设的前项和为,令,求.18.(本题满分12分)如图,三棱柱中,侧棱平面,为等腰直角三角形,,且分别是的中点(1)求证:平面;(2)求锐二面角的余弦值.19.(本题满分12分)某工厂生产某种零件,每天生产成本为1000元,此零件每天的批发价和产量均具有随机性,且互FEC1B1A1CBA不影响.其具体情况如下表:日产量400500批发价810概率0.40.6概率0.50.5(1)设随机变量X表示生产这种零件的日利润,求X的分布列及期望;(2)若该厂连续3天按此情况生产和销售,设随机变量Y表示这3天中利润不少于3000的天数,求Y的数学期望和方差,并求至少有2天利润不少于3000的概率.(注:以上计算所得概率值用小数表示)20.(本题满分12分)已知抛物线,过焦点且斜率为1的直线交抛物线C于两点,以线段为直径的圆在轴上截得的弦长为.(1)求抛物线的方程;(2)过点的直线交抛物线C于F、G两点,交轴于点D,设试问是否为定值?若是,求出该定值;若不是,说明理由.21.(本题满分12分)已知函数(1)当时,求函数的极值;(2)当时,若对,当时,函数的最小值为,求a的取值范围.请考生在(22).(23).(24)三题中任选一题作答,如果多答,则按做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑.22.(本小题满分10分)选修4—1:几何证明选讲如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B.C,的平分线分别交AB.AC于点D.E.(1)证明:.(2)若AC=AP,求的值.23.(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系中,曲线C的参数方程为,直线的参数方程为.以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.(1)求曲线C的直角坐标方程和直线的极坐标方程;(2)若为曲线C上的动点,求点P到直线的距离d的最大值和最小值.24.(本小题满分10分)选修4—5:不等式选讲已知关于的不等式的解集是(1)求的值;(2)若均为正实数,且,求的最小值.数学试题答案(理)一、选择题1-5:DBCDC6-10:CBADB11-12:BB二、填空题:13.-2014.915.16.17.解:(1)公差,………2分∴∴∴………4分设等比数列的公比为 ∴即∴即………6分(2)由得:∴即………8分∴=………10分==………12分18.(1)连结, 是等腰直角三角形斜边的中点,∴.又三棱柱为直三棱柱,∴面面,∴面,.………2分设,则.∴,∴.………4分又,∴平面.………6分(2)以为坐标原点,分别为轴建立直角坐标系如图,...