山东省济南鱼台一中高二数学5月开学考试试卷答案 山东省济南鱼台一中高二数学5月开学考试试卷 山东省济南鱼台一中高二数学5月开学考试试卷VIP免费

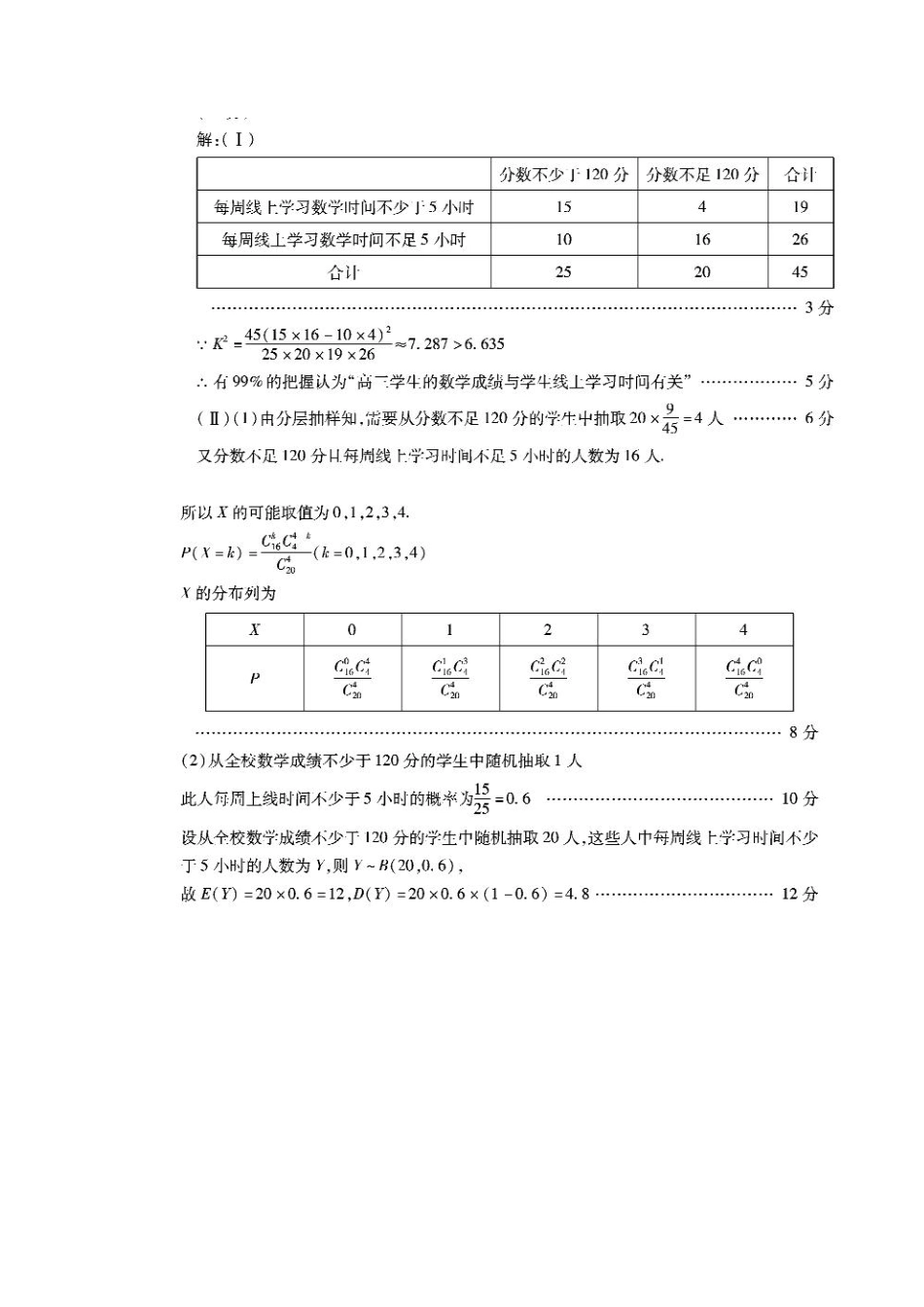
高二数学试题答案选择题123456789101112BAADACCCABABCACBC填空题13.1414.315.124116.0.1817.解：（1）二项式32()nxx展开式中的通项公式为413(2)nrrrrnTCx，第4项是为12333(2)nnCx是常数项，1203n，12n．（2）要使展开式中的项为有理项，需1234r为整数，故有0,3,6,9,12r，故展开式中有理项共有5项．18.解(1)记“从这12天的数据中随机抽取3个，至多有1天的用水量超标”为事件A，则P(A)＝C14C28C312＋C38C312＝168220＝4255.(2)以这12天的样本数据中用水量超标的频率作为概率，易知用水量超标的概率为13.X的所有可能取值为0,1,2,3，易知X～B3，13，P(X＝k)＝Ck313k233－k，k＝0,1,2,3，则P(X＝0)＝827，P(X＝1)＝49，P(X＝2)＝29，P(X＝3)＝127.∴随机变量X的分布列为X0123P8274929127数学期望E(X)＝3×13＝1，方差D(X)＝3×13×1－13＝23.19.解：（1）已知变量x，y具有负相关关系，故乙不对．∵，，代入甲和丙的回归方程验证甲正确；（2）∵0.9702＞0.9524，且R2越大，残差平方和越小，拟合效果越好，∴选用+0.875x+90.25更好；20．解：（1）记事件A：“该生英语等级考试成绩为优”，则1()4PA，事件B：“该生直到高二下期英语等级考试成绩才为优”，所以33127()()()44256PBPAAAA．（2）2~(6,)3XB，6621()()()(0,1,2,,6)33kkkPXkCkX0123456P172912729202431607298024364243647292()643EX．21.解：（1）由题意得()fx的定义域为(0,)，221()axafxxxx，①当0a时，()0fx，故()fx在上为增函数；②当0a时，由()0fx得xa；由()0fx得xa；由()0fx得xa；()fx在(0，]a上为减函数，在(,)a上为增函数．综上，当0a时，()fx在(0,)上是增函数；当0a时，()fx在(0，]a上是减函数，在(,)a上是增函数．（2）由（1）知，当ae时，()fx在[1，]e上单调递减，()minfxf（e）11aee，解得2ae，2ae．22