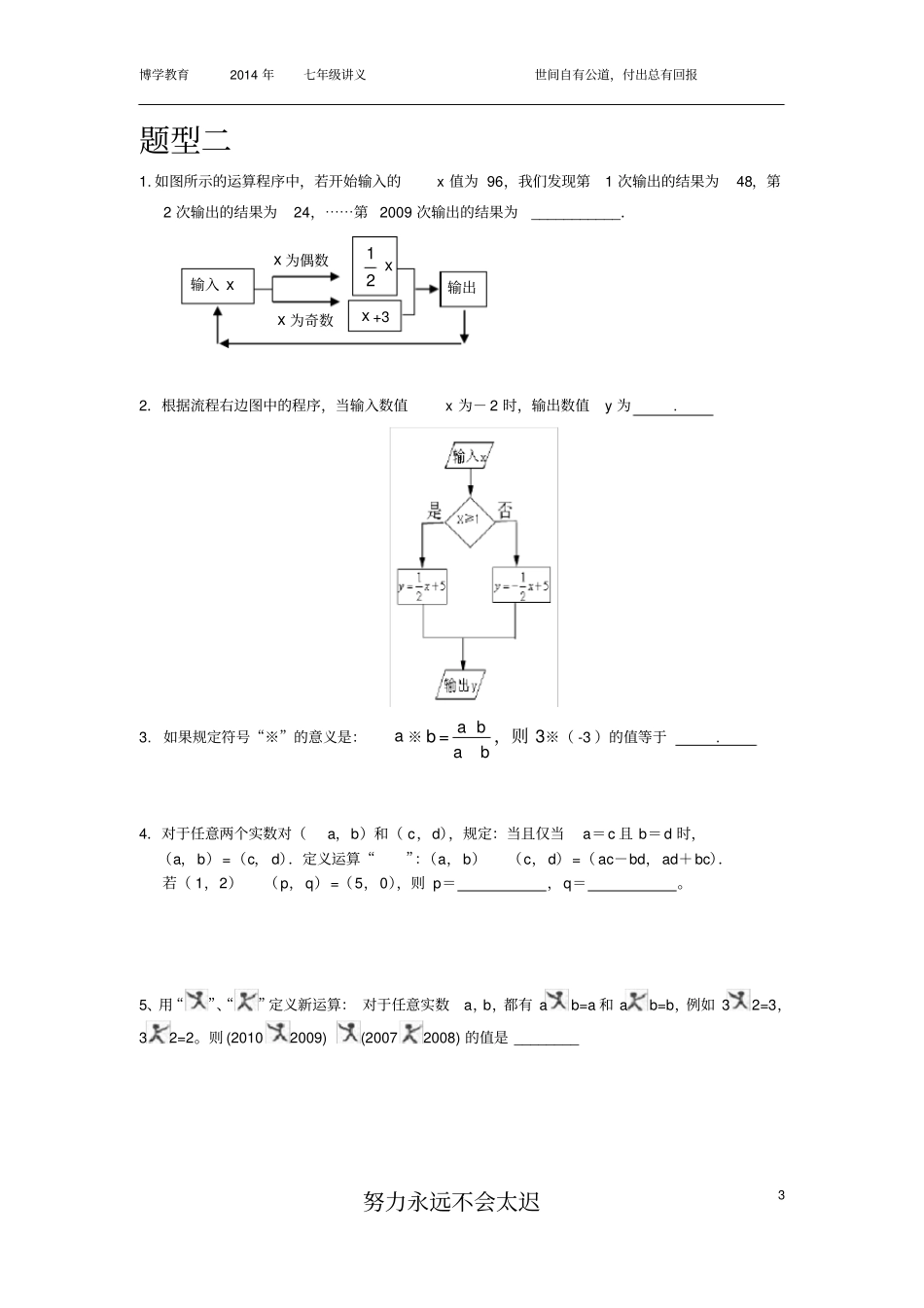
博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟1难题先讲1.有一列数:第一个数是x1=1,第二个数x2=3,第三个数开始依次记为x3、x4、⋯⋯从第二个数开始,每个数是它相邻两数和的一半。(1)则第三、四、五个数分别为_________、_________、_______;(2)推测x10=;(3)猜想第n个数xn=.2.将连续的奇数1、3、5、7⋯⋯排成如图所示的数阵:1357911131517192123252729313335373941434547495153555759⋯⋯(1)如图,十字框中五个数的和与框正中心的数17有什么关系?(2)若将十字框上下、左右平移,可框住另外五个数,这五个数的和与框正中心的数还有这种规律吗?请说明理由.(3)十字框中五个数的和能等于2007吗?若能,请写出这五个数;若不能,请说明理由.3.如图的数阵是由一些奇数组成的。(1)形如图框中的四个数有什么关系?(可设第一行的第一个数为x,用含x的代数式表示另外三个数即可)。(2)若这样框中的四个数的和是200,求出这四个数。(3)是否存在这样的四个数,它们的和为2010..若存在,请求出这四个数中最大的数,若不存在请说明理由。博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟2题型一1.已知(a+2)2+b-12=0,求5a2b—[2a2b-(ab2-2a2b)-4]-2ab2的值2.2222(3)[5()2]mnmmmnmmn.其中2120mn.3.若m-n=4,mn=-1,求(-2mn+2m+3n)-(3mn+2n-2m)-(m+4n+mn)的值。博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟3题型二1.如图所示的运算程序中,若开始输入的x值为96,我们发现第1次输出的结果为48,第2次输出的结果为24,⋯⋯第2009次输出的结果为___________.2.根据流程右边图中的程序,当输入数值x为-2时,输出数值y为.3.如果规定符号“※”的意义是:a※b=baba,则3※(-3)的值等于.4.对于任意两个实数对(a,b)和(c,d),规定:当且仅当a=c且b=d时,(a,b)=(c,d).定义运算“”:(a,b)(c,d)=(ac-bd,ad+bc).若(1,2)(p,q)=(5,0),则p=,q=。5、用“”、“”定义新运算:对于任意实数a,b,都有ab=a和ab=b,例如32=3,32=2。则(20102009)(20072008)的值是________输入x12xx+3输出x为偶数x为奇数博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟4题型三1.已知3nm,522mn。2.如果代数式-2a+3b+8的值为18,那么代数式9b-6a+2的值等于_______3.若代数式2x2+3x+7的值为8,则代数式4x2+6x-9的值是_________4.已知多项式935cxbxax,当x=-1时,多项式的值为17,则该多项式当x=1时的值是.5.当x=-3时,315mxnx的值是-5,则x=3时,这个代数式的值是_______.6.当x=2时,代数式ax3+bx+1的值为3,那么当x=-2时,代数式ax3+bx+1=_______博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟5题型四1.已知A=5x2+4x–1,B=–x2–3x+3,C=8–7x–6x2,求A–B+C的值.2.化简:已知A=-3x3+2x2-1,B=x3-2x2-x+4,求2A-(A-B).3.已知A=2a2-a,B=-5a+1,当a=12时,求代数式3A-2B+1的值(4分)博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟6题型五1.当m=_________时,多项式3x2+2xy+y2–mx2中不含x2项。2、若关于a,b的多项式2222223bmabababa不含ab项,则m=。3、已知多项式(2mx2+5x2+3x+1)―(5x2―4y2+3x)化简后不含x2项.求多项式2m3―[3m3―(4m―5)+m]的值.4..已知:关于x、y的多项式mx3+3nxy2-2x3-xy2+y中不含三次项,求代数式2m+3n的值?5.已知A=b12ayy,B=110322yayy,且多项式2A-B的值与字母y的取值无关,求2222222132,abababab的值。博学教育2014年七年级讲义世间自有公道,付出总有回报努力永远不会太迟7题型六1.已知12xab与34ab是同类项、222ab的系数为y、13mab的次数是4:先分别求出x、y、m,然后计算44262xyxmy的值2.化简与求值:(1)当23mn时,求代数式2(2)2(2)1mnmn的值;(2)当534mn时,求代数式2()4(2)2mnmn的值;(3)求整式332373(2)aababa与323(63)2(5)ababaa的和,并说明当a、b均为无理数时,结果是一个什么数?博学教育2014年七年级讲义世间自...