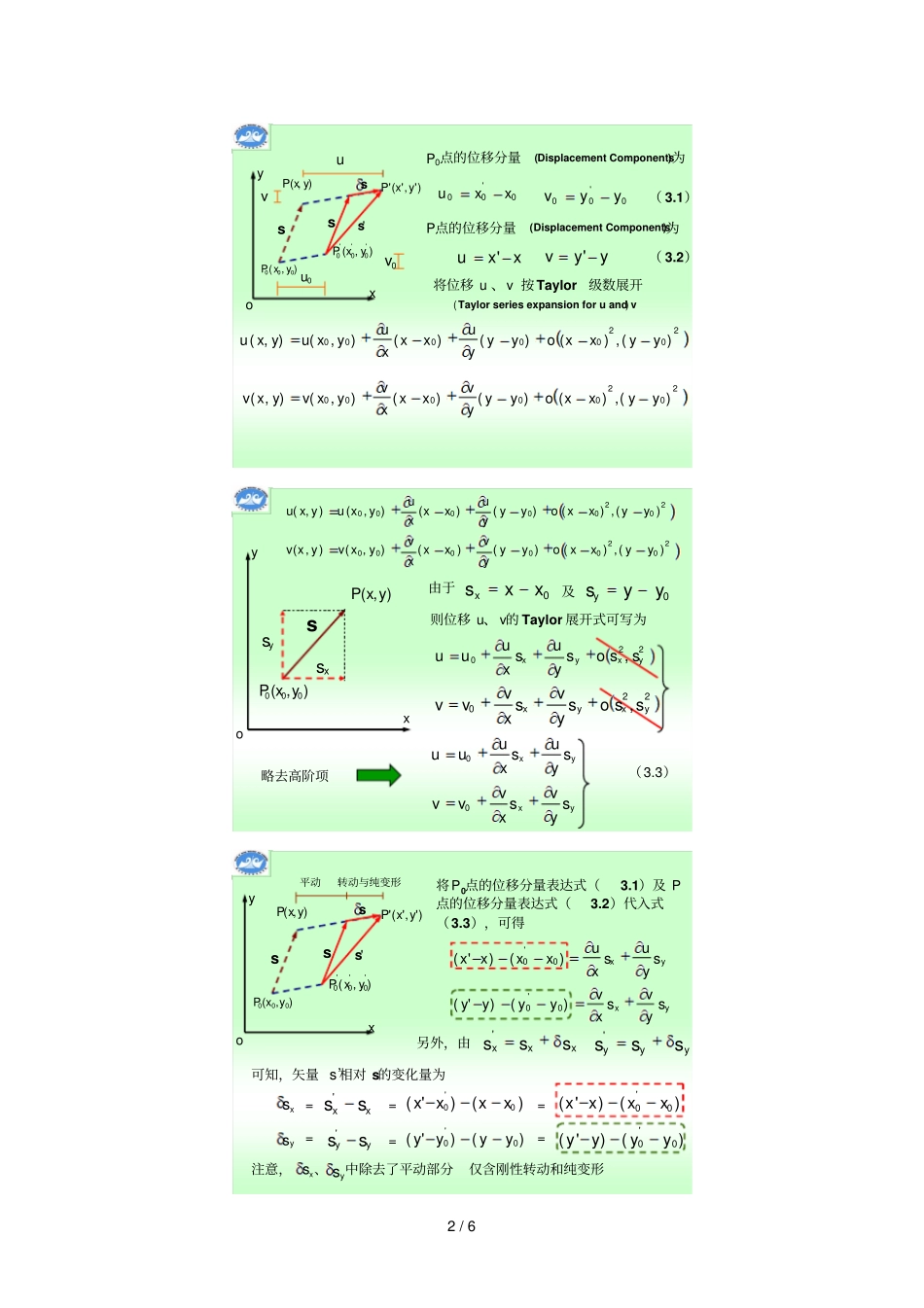
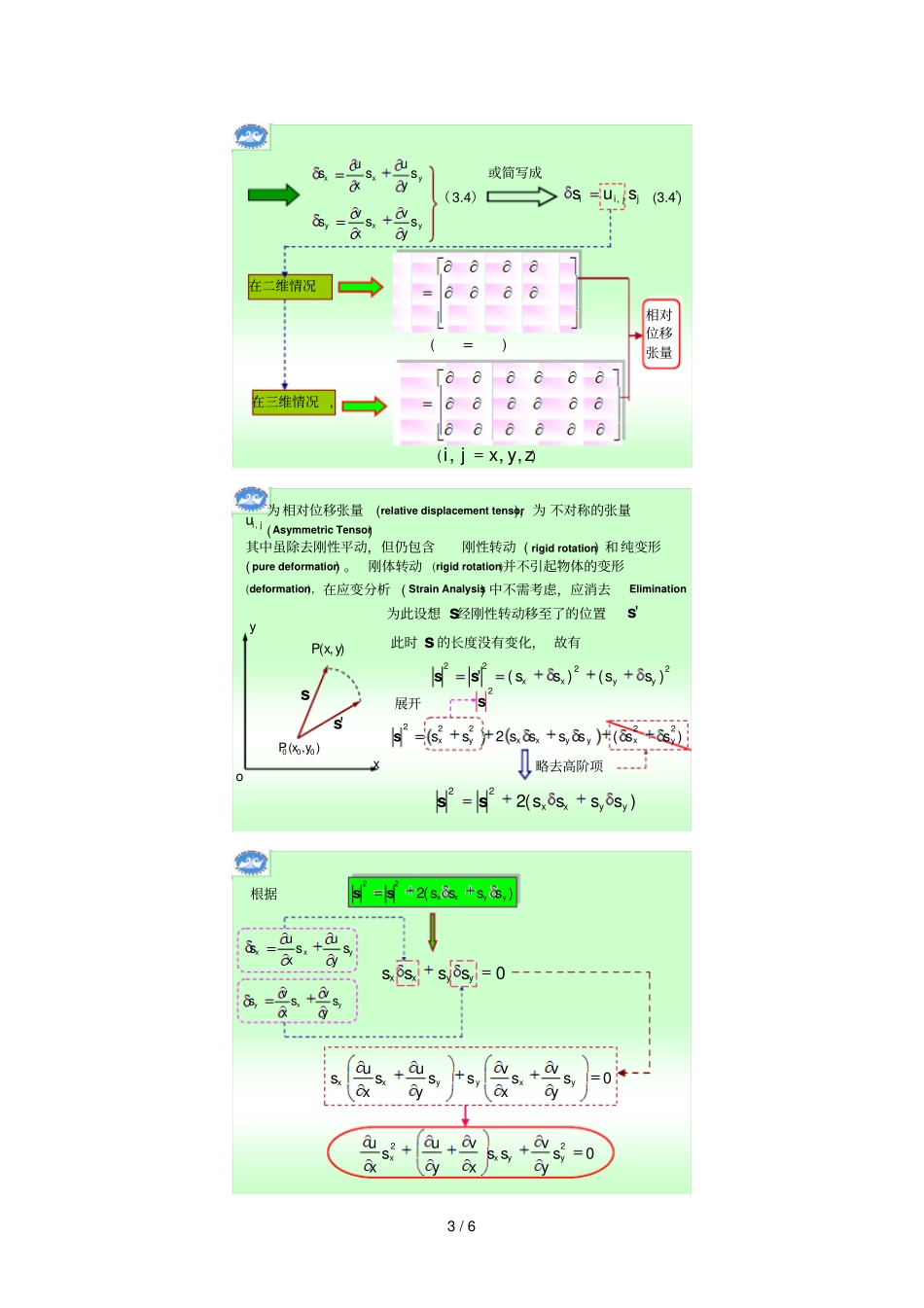
1/6第3章应变分析(StrainAnalysis)本章在讨论物体的应力之后,研究受力物体的变形和应变。在外力(ExternalForce)作用下,物体各点的位置要发生变化,即发生位移(Displacement)。物体内一点的位移由刚性位移(平动加转动)和变形位移(又含平动和转动及纯变形)组成。在此主要讨论物体的变形位移§3.1变形与应变的概念TheConceptofDeformationandStrain如图3.1所示的一弹性体受力后发生图示变形,其中任意一点的位移分量为坐标的函数,即AxyzoA),,(zyxuu),,(zyxvv),,(zyxww如果知道了物体内一点的位移分量,根据几何方程,该点的变形也就确定了为此首先研究物体中任意微段的变形状态,进一步引出应变的概念。如图3.2所示,在oxy平面内变形前物体相邻两点p0(x0,y0)和p(x,y)间的线段为p0p=soxy),(000yxP),(yxP)','('yxP),('0'0'0yxPss'ss'''0sPP变形后该线段两端分别移到和用线段),('0'0'0yxP)','('yxP表示s沿x,y轴的分量为sx,sys’的分量为xxxsss'yyysss'2/6oxy),(000yxP),(yxP)','('yxP),('0'0'0yxPss'ssP0点的位移分量(DisplacementComponents)为0'00xxu0'00yyv(3.1)P点的位移分量(DisplacementComponents)为xxu'yyv'(3.2)将位移u、v按Taylor级数展开(Taylorseriesexpansionforuandv)20200000)(,)()()(),(),(yyxxoyyyuxxxuyxuyxu20200000)(,)()()(),(),(yyxxoyyyvxxxvyxvyxv0u0vuvoxy),(000yxP),(yxPs0xxsx0yysyxsys由于及则位移u、v的Taylor展开式可写为220,yxyxssosyusxuuu220,yxyxssosyvsxvvv略去高阶项yxsyusxuuu0yxsyvsxvvv0(3.3)20200000)(,)()()(),(),(yyxxoyyyuxxxuyxuyxu20200000)(,)()()(),(),(yyxxoyyyvxxxvyxvyxvoxy),(000yxP),(yxP)','('yxP),('0'0'0yxPss'ss将P0点的位移分量表达式(3.1)及P点的位移分量表达式(3.2)代入式(3.3),可得yxsyusxuxxxx)()'(0'0yxsyvsxvyyyy)()'(0'0另外,由可知,矢量s’相对s的变化量为xxxsss'yyysss')()'(0'0xxxx=xsxxss'=)()'(0'0xxxx=ysyyss')()'(0'0yyyy)()'(0'0yyyy===注意,、中除去了平动部分仅含刚性转动和纯变形xsys平动转动与纯变形3/6yxxsyusxusyxysyvsxvs(3.4)或简写成jjiisus,(3.4’)在二维情况在三维情况,()()zyxji,,,相对位移张量jiu,为相对位移张量(relativedisplacementtensor),为不对称的张量(AsymmetricTensor)其中虽除去刚性平动,但仍包含刚性转动(rigidrotation)和纯变形(puredeformation)。oxy),(000yxP),(yxPs刚体转动(rigidrotation)并不引起物体的变形's为此设想经刚性转动移至了的位置s's此时的长度没有变化,s故有2222)()('yyxxssssss)(222222yxyyxxyxsssssssss展开略去高阶项2s)(222yyxxssssss(deformation),在应变分析(StrainAnalysis)中不需考虑,应消去Elimination)(222yyxxssssss根据0yyxxssssyxxsyusxusyxysyvsxvs022yyxxsyvssxvyusxu0yxyyxxsyvsxvssyusxus4/6xsys由于、的任意性,0yvxu0xvyu同理,当在oyz和oxz平面讨论时,可得0zw0zvywxwzuijjiuu,,对应于刚体转动的相对位移张量,必为反对称张量。对应于刚体转动的相对位移张量,必为反对称张量。任何一个二阶张量都可以唯一分解成一个对称张量和一个反对称张量任何一个二阶张量都可以唯一分解成一个对称张量和一个反对称张量)(21)(21,,,,,ijjiijjijiuuuuu反对称部分刚体转动对称部分纯变形将)(21)(21,,,,,ijjiijjijiuuuuu写成张量形式为ijijjiu,此处应变张量(纯变形)转动张量对于纯变形来说0ij(3.12)ijjiu,则方程jjiisus,可化为jijiss现说明应变张量的物理意义ijoxysl)如平行于x轴sssx0ysssssxxxxx与x平行的矢量的单位长度的伸长或压缩,称为线应变同理可知和的物理意义也是线应变yz5/62)如有两个矢量、变形前分别平行于ox、oy轴1s2syxo1s2s11iss22jss变形后为'1s'2s'1s'2sxs1ys1xs2ys2'1s=)(11ssix+ysj1'2sxsi2+)(22ssjy'1s'2s令与的夹角为则由两矢量的内积定义,有cos'2'1'2'1ssssyxo1s2s'1s'2sxs2ys2ys1xs1同时:'2'1ss)()('2'2'1'1jsisjsisyxyx='2'1'2'1yyxxssss其中:yyss1'1'1ysxxss2'2'2xsyyxxssssss122211'2'1)()(ss因S1、S2均为小量,故略去δS的二次微量后,得yxssss1221'2'1ss'1s'2s与的矢量内积为已知:1122'2'...