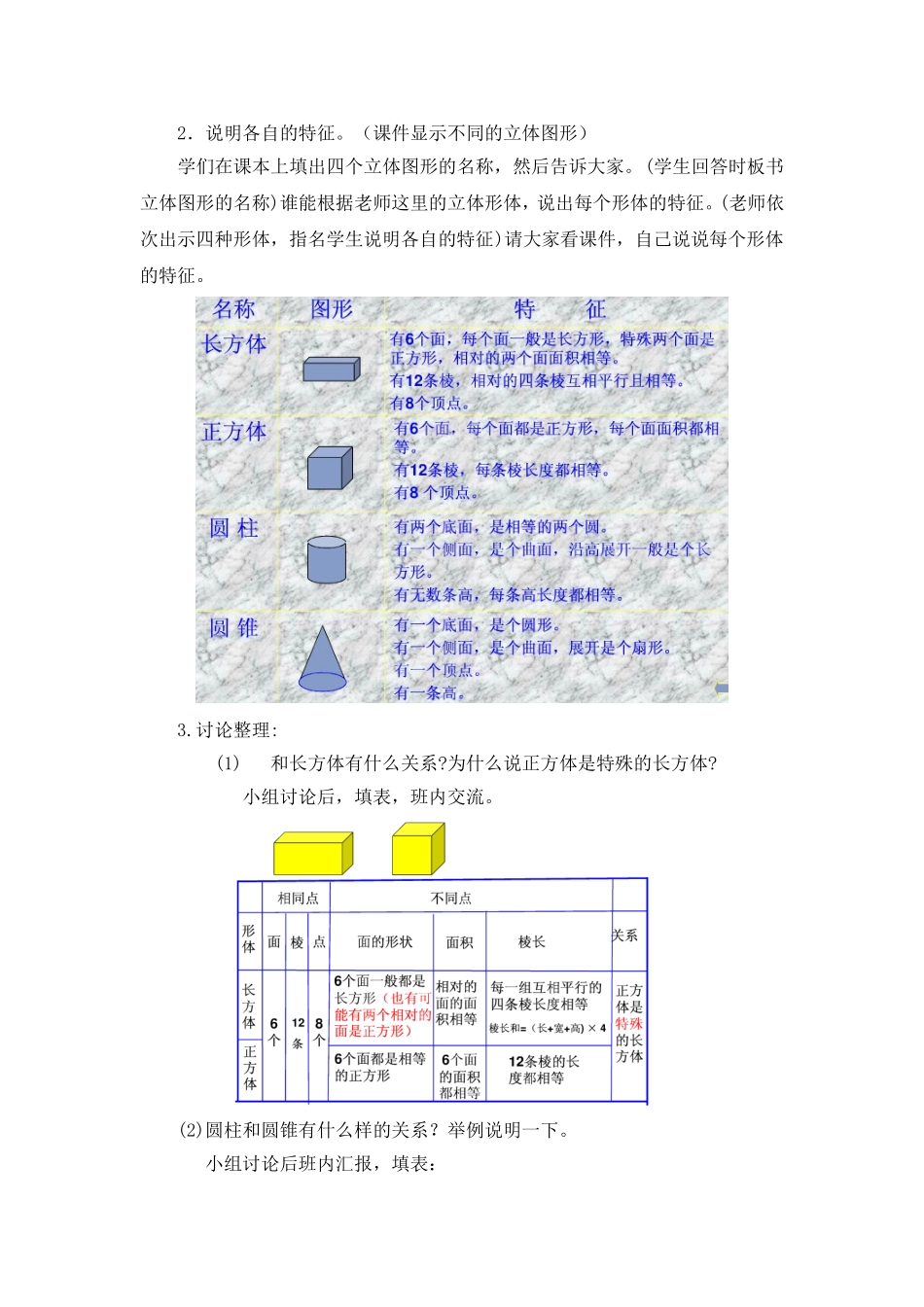
立体图形的特点、联系及面积的计算教学内容:青岛版P103第二个红点,P105t1-t3,t10,t13,t19教学要求1.使学生进一步认识学过的一些立体图形的特征,发展学生的空间观念。2.使学生加深理解长方体、正方体和圆柱体表面积的计算方法,能根据已知条件计算这些立体图形的表面积。教学重、难点教学重点:整理、复习立体图形的特征,掌握他们的表面积的计算方法。教学难点:沟通立体图形体积计算方法之间的联系教具、学具准备师生都准备长方体、正方体、圆柱和圆锥各一个,课件。教学过程一、揭示课题教师导入:我们已经复习了平面图形的相关知识,今天我们来复习立体图形的特点、联系及面积的计算。(板书课题)二、复习立体图形的特征1.提问:我们学习过哪些立体图形?谁来拿出不同的立体形体,告诉大家各是什么名称。2.说明各自的特征。(课件显示不同的立体图形)学们在课本上填出四个立体图形的名称,然后告诉大家。(学生回答时板书立体图形的名称)谁能根据老师这里的立体形体,说出每个形体的特征。(老师依次出示四种形体,指名学生说明各自的特征)请大家看课件,自己说说每个形体的特征。3.讨论整理:(1)和长方体有什么关系?为什么说正方体是特殊的长方体?小组讨论后,填表,班内交流。(2)圆柱和圆锥有什么样的关系?举例说明一下。小组讨论后班内汇报,填表:三、表面积计算1.复习表面积的意义。提问:什么是立体图形的表面积?请同学们拿出立体图形,看着这些形体,一边用手摸一边说出每个形体的表面积包括哪几部分的面积,师生整理:提问:圆柱体表面积是哪些面面积的和?师生共同整理:2.复习圆柱的侧面积。圆柱的侧面展开是什么形状?侧面展开的长方形的长、宽与圆柱有什么联系?圆柱的侧面积怎样算?3.归纳表面积计算方法。请同学们根据立体图形的表面积是围成立体图形所有面的面积的和这个意义,在课本上用字母表示出计算每个图形表面积的方法。指名学生依次口答归纳出的表面积计算方法,老师在黑板上板书出来,并让学生说一说是怎样想的。长方体的表面积=(上面+前面+侧面)×2S=(ab+ah+bh)×2正方体的表面积=一个面的面积×6S=a2×6圆柱的表面积=侧面积+底面积×2S=ch+2∏r24.做“练一练”三道题。指名三人板演,其余学生在练习本上列出三道题的算式。集体订正,让学生说明每一步求的什么。四、综合练习1.做P105t1-3。让学生默读题目。提问:如何描述立体图形的大小、形状和位置?试举例说明。找两个同学上台演示1题“我说你搭”。学生评议。小组合作完成2.3题2.小组合作完成第10题。提问:通风管的表面由哪几个面组成?怎么求每个面的面积?意图:引导说出本题的表面积就是圆柱的侧面积,让学生感知表面积在实际中的灵活应用。3.自主练习:意图:引导学生观察灯罩,确定灯罩的表面积=灯罩的侧面积,没有封闭的上下底。再次强化学生对于实际生活中的表面积的认识。4.学生自主练习:提问:“占地面积”是什么意思?是哪个面占地的?意图:分清“表面积”中各面和“占地面”的区别,引导学生理清概念,建立系统认识。五、课堂总结。谈话:今天我们回顾了立方体的相关知识,你有什么收获,能和大家分享吗意图:让学生分享学习成功的喜悦,激发学生的积极性和求知欲,同时也为学生的后续学习总结了经验和方法。板书设计立体图形的特点、联系及面积的计算长方体的表面积=(上面+前面+侧面)×2S=(ab+ah+bh)×2正方体的表面积=一个面的面积×6S=a2×6圆柱的表面积=侧面积+底面积×2S=ch+2∏r2使用说明:1.教学反思。本节课的教学设计主要体现了以下四点:(1)模块化复习,我把本课复习内容分几大模块进行:从认识图形到复习各种形体的特征,再到种种形体间的区别与联系,最后复习表面积。这样有利于学生知识的系统化和完整性。(2)同时,本节课以学生的知识经验和知识背景为切入点,引导学生进行积极的操作和体验。在这个过程中,教师引导学生感知、感受、感悟知识,围绕着学生这个主体,利用现代化教学手段与常规教学手段互相结合的方式,直观展现了知识的形成过程,启迪学生思维,提高了课堂效率。(3)本课以学生的自主学习为活动前提,创设有助于学生自主学习、合作交流的学习...