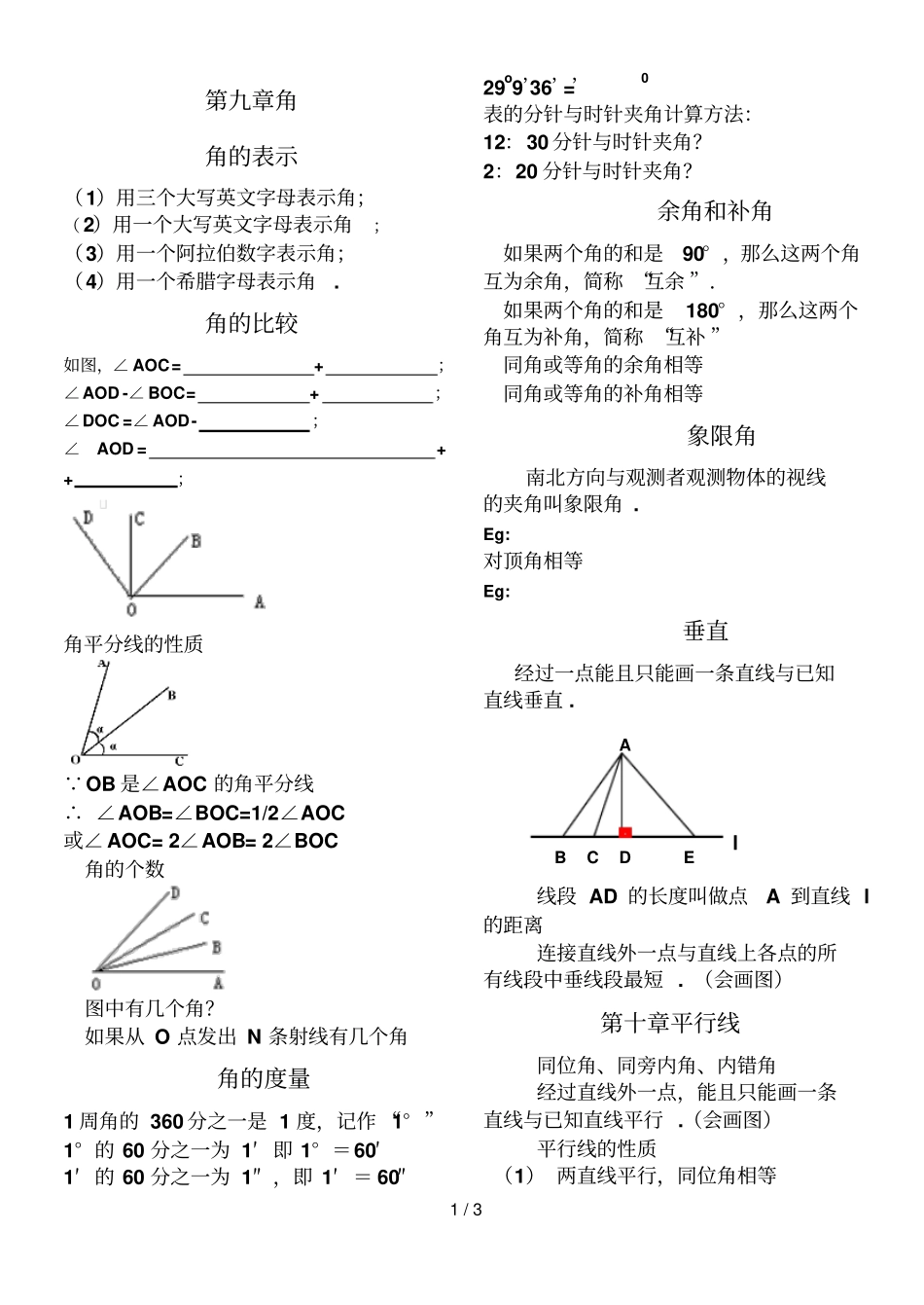
1/3第九章角角的表示(1)用三个大写英文字母表示角;(2)用一个大写英文字母表示角;(3)用一个阿拉伯数字表示角;(4)用一个希腊字母表示角.角的比较如图,∠AOC=+;∠AOD-∠BOC=+;∠DOC=∠AOD-;∠AOD=++;角平分线的性质∵OB是∠AOC的角平分线∴∠AOB=∠BOC=1/2∠AOC或∠AOC=2∠AOB=2∠BOC角的个数图中有几个角?如果从O点发出N条射线有几个角角的度量1周角的360分之一是1度,记作“1°”1°的60分之一为1′即1°=60′1′的60分之一为1″,即1′=60″29o9’36’’=0表的分针与时针夹角计算方法:12:30分针与时针夹角?2:20分针与时针夹角?余角和补角如果两个角的和是90°,那么这两个角互为余角,简称“互余”.如果两个角的和是180°,那么这两个角互为补角,简称“互补”同角或等角的余角相等同角或等角的补角相等象限角南北方向与观测者观测物体的视线的夹角叫象限角.Eg:对顶角相等Eg:垂直经过一点能且只能画一条直线与已知直线垂直.线段AD的长度叫做点A到直线l的距离连接直线外一点与直线上各点的所有线段中垂线段最短.(会画图)第十章平行线同位角、同旁内角、内错角经过直线外一点,能且只能画一条直线与已知直线平行.(会画图)平行线的性质(1)两直线平行,同位角相等ABCDEl2/3(2)两直线平行,内错角相等(3)两直线平行,同旁内角互补平行线的判定(1)同位角相等,两直线平行(2)内错角相等,两直线平行(3)同旁内角互补,两直线平行(4)平行于同一直线的两直线平行(5)垂直于同一直线的两直线平行如果两条直线平行,那么其中一条直线上每一点到另一条直线的距离都相等,这个距离,中做这两条平行线之间的距离.三角形1.表示三角形时,字母没有先后顺序如下图三角形表示为△2.如下图,我们把BC(或a)叫做A的对边,把AB(或c)、AC(或b)分别叫做A的邻边.三角形的分类三角形按边分类:不等边三角形三角形底边和腰不等的三角形等腰三角形等边三角形三角形按角分类:锐角三角形三角形直角三角形钝角三角形三角形的三边关系:三角形中任意两边的和大于第三边如果三角形其中两边为a,b则另一边x取值范围为a-b<x<a+b.三角形的三线三角形的中线三角的中线交于三角形的内部三角形的角平分线三角形的角平分线交于三角形的内部三角形的高三角形的一个外角等于与它不相邻的两个内角的和多边形N边形有条对角线各边相等,内角也等的多边形叫正多边形多边形从一个顶点可以画(n-2)条对角线,可以把多边形分为(n-2)个三角形正多边形内角和等于(n-2)×180o多边形外角和等于360o多边形的密铺当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角时,就能拼成一个平面图形(铺满地面).任意三角形,四边形都能形成密铺正多边形密铺组合单个正多边形正三角形、正方形、正六边能形成密铺两多边形能形成密铺的有:正方形正三角形和正六边形正十二边形正方形和正八边形特例:正五边形与正十边形角能拼成3600但是不能形成密铺三个多边形能形成密铺的有:正三角形、正方形和正六边形正方形、正六边形和正十二边形圆圆的描述的定义:在一个平面内,线段OA饶它的一个端点O旋转一周,另一个端点A随之旋转所形成的的图形叫做圆.固定的端点O叫做圆心,线段OA叫做半径.如图:以O为圆心的圆,记作“⊙O”,读作“圆O”圆的集合的定义:圆是平面内到定点的距3/3离等于定长的点的集合.请你用集合的语言描述下面的两个概念:(1)圆的内部是点的集合(2)圆的外部是点的集合弧的表示方法:(如图)优弧(只能用三个字母表示)劣弧(可用三个,也可用两个字母)在同圆与等圆中,能够互相重合的弧叫等弧等圆:能够重合的圆同心圆:圆心相同的圆两个同心圆之间的部分叫圆环,大圆的半径为2r,小圆半径为r,则圆环与大圆的面积比为:S大圆=π(2r)2=4πr2S小圆=πr2S环=4πr2-πr2=3πr2S大圆:S环=4πr2:3πr2=4:3尺规作图尺子没有刻度的尺子基本作图:(1)作一条线段等于已知线段(2)作一角等于已知角求作三角形:已知及两边夹角:已知及两夹边:已知三边: