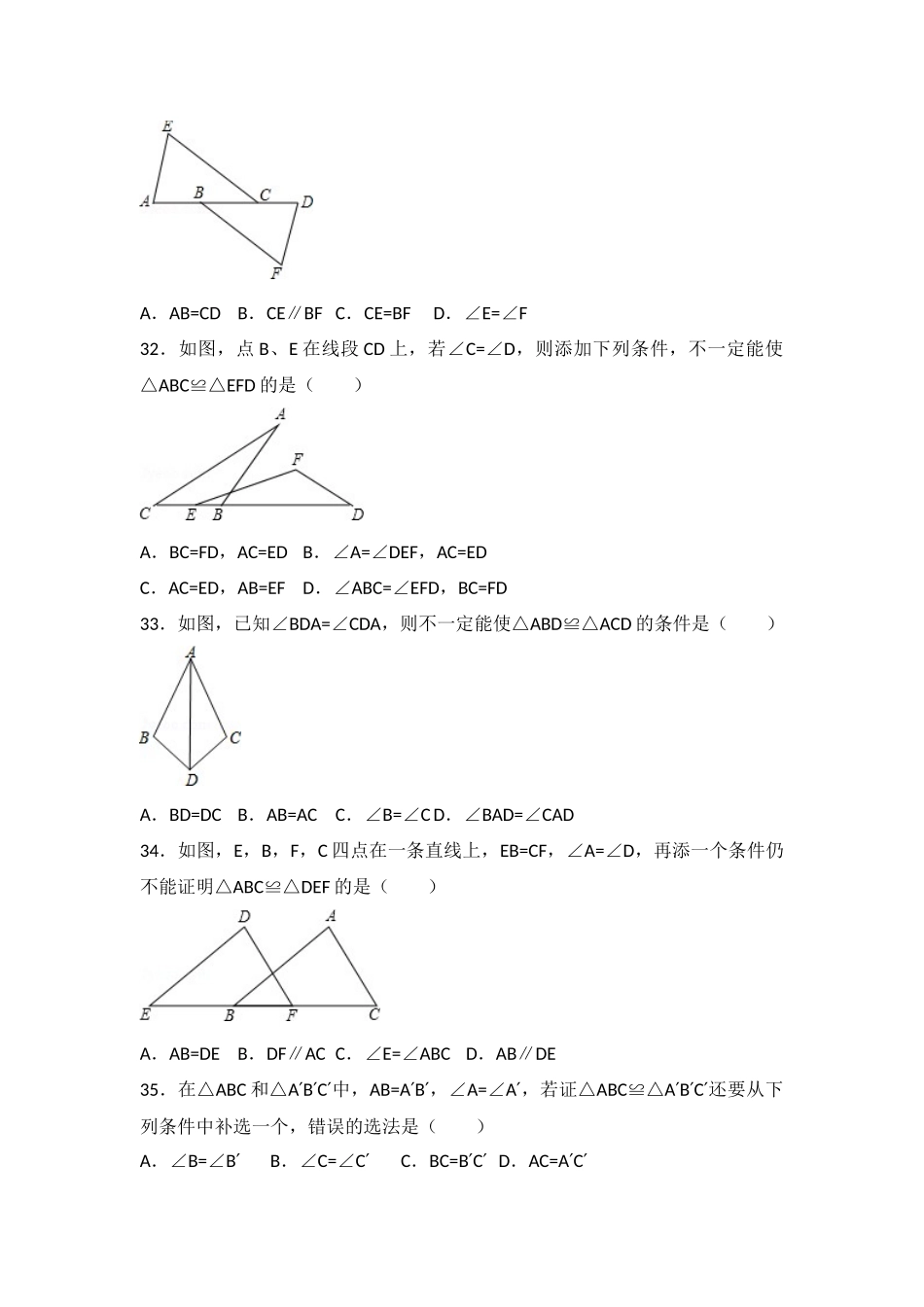
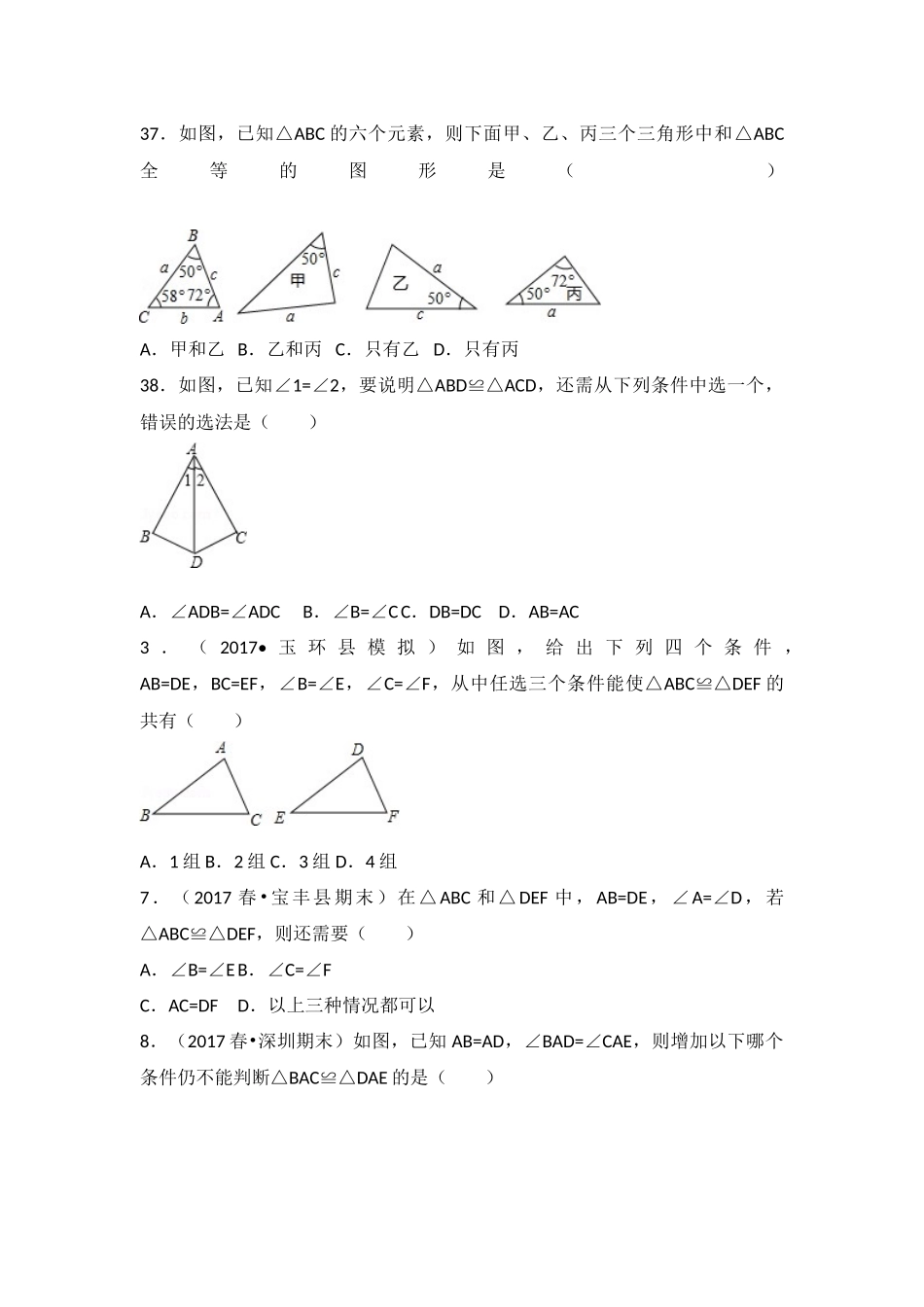
全等三角形的判定(AAS)7.在△ABC和△DEF中,AB=DE,∠A=∠D,若△ABC≌△DEF,则还需要()A.∠B=∠EB.∠C=∠FC.AC=DFD.以上三种情况都可以21.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是()A.AC=BDB.∠CAB=∠DBAC.∠C=∠DD.BC=AD22.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是()A.AB=DEB.AC=DFC.∠A=∠DD.BF=EC27.如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是()A.∠D=∠CB.BD=ACC.∠CAD=∠DBCD.AD=BC30.如图,AE∥DF,AE=DF.则添加下列条件还不能使△EAC≌△FDB.()A.AB=CDB.CE∥BFC.CE=BFD.∠E=∠F32.如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是()A.BC=FD,AC=EDB.∠A=∠DEF,AC=EDC.AC=ED,AB=EFD.∠ABC=∠EFD,BC=FD33.如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是()A.BD=DCB.AB=ACC.∠B=∠CD.∠BAD=∠CAD34.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DEB.DF∥ACC.∠E=∠ABCD.AB∥DE35.在△ABC和△ABC′′′中,AB=AB′′,∠A=∠A′,若证△ABC≌△ABC′′′还要从下列条件中补选一个,错误的选法是()A.∠B=∠B′B.∠C=∠C′C.BC=BC′′D.AC=AC′′37.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲和乙B.乙和丙C.只有乙D.只有丙38.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是()A.∠ADB=∠ADCB.∠B=∠CC.DB=DCD.AB=AC3.(2017•玉环县模拟)如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有()A.1组B.2组C.3组D.4组7.(2017春•宝丰县期末)在△ABC和△DEF中,AB=DE,∠A=∠D,若△ABC≌△DEF,则还需要()A.∠B=∠EB.∠C=∠FC.AC=DFD.以上三种情况都可以8.(2017春•深圳期末)如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是()A.AC=AEB.BC=DEC.∠B=∠DD.∠C=∠E9.(2017春•黄岛区期末)如图,已知∠ABC=∠DCB,添加下列条件,△ABC与△DCB不能全等是()A.AC=DBB.AB=DCC.∠A=∠DD.∠1=∠211.(2017春•乳山市期末)如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是()A.∠B=∠CB.BE=CDC.AB=ACD.∠CEB=∠BDC12.(2017春•胶州市期末)如图,AC,BD交于点O,∠ABC=∠DCB,下列条件中不能判定△ABC≌△DCB的是()A.∠ACB=∠DBCB.AC=DBC.AB=DCD.∠A=∠D16.(2017春•永定区期中)如图,DB⊥AE,AB=DB,AC=DE.则△ABC≌△DBE的依据是()A.SASB.ASAC.AASD.HL19.(2016•新疆)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是()A.∠A=∠DB.BC=EFC.∠ACB=∠FD.AC=DF21.(2016•金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是()A.AC=BDB.∠CAB=∠DBAC.∠C=∠DD.BC=AD21.(2016•金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是()A.AC=BDB.∠CAB=∠DBAC.∠C=∠DD.BC=AD27.(2016•长沙模拟)如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是()A.∠D=∠CB.BD=ACC.∠CAD=∠DBCD.AD=BC30.(2016•琼海校级模拟)如图,AE∥DF,AE=DF.则添加下列条件还不能使△EAC≌△FDB.()A.AB=CDB.CE∥BFC.CE=BFD.∠E=∠F33.(2016•闸北区二模)如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是()A.BD=DCB.AB=ACC.∠B=∠CD.∠BAD=∠CAD34.(2016秋•巫溪县期末)如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DEB.DF∥ACC.∠E=∠ABCD.AB∥DE35.(2016秋•西青区校级期末)在△ABC和△ABC′′′中,AB=...