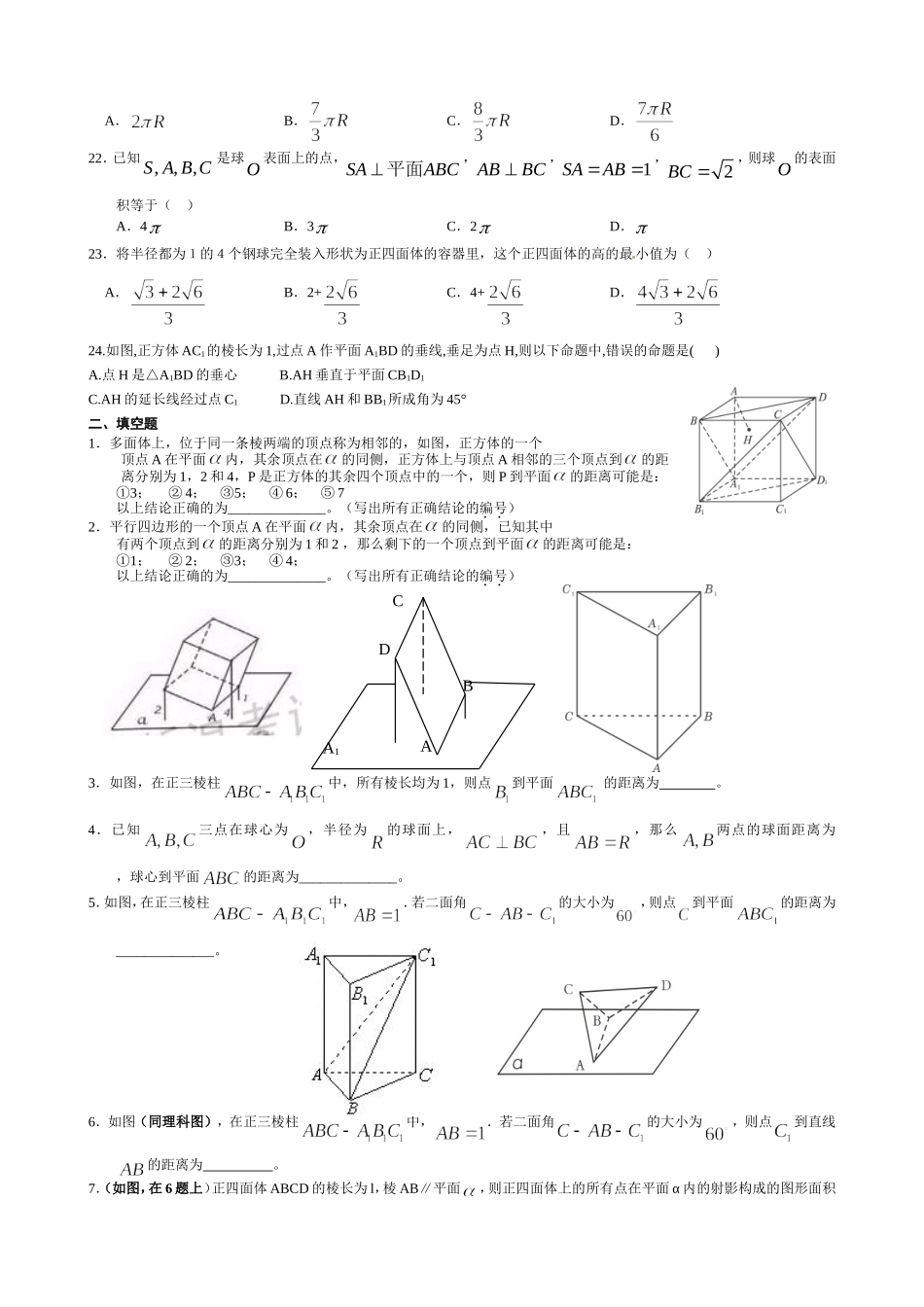
高一数学点直线平面之间的位置关系强化练习题一、选择题1.已知平面外不共线的三点到的距离都相等,则正确的结论是()A.平面必平行于B.平面必与相交C.平面必不垂直于D.存在的一条中位线平行于或在内2.给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,lα,mβ,则αβ;∥②若αβ,l∥α,mβ,则lm;∥③若α∩β=l,β∩γ=m,γ∩α=n,lγ,∥则mn.∥其中真命题的个数为()A.3B.2C.1D.03.如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是()(A)48(B)18(C)24(D)364.已知二面角的大小为,为异面直线,且,则所成的角为()(A)(B)(C)(D)5.如图,点P在正方形ABCD所在的平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为()A.30°B.45°C.60°D.90°7.设、是两条不同的直线,、是两个不同的平面.考查下列命题,其中正确的命题是()A.B.C.D.8.设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是()A.AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若AB=AC,DB=DC,则AD=BCD.若AB=AC,DB=DC,则ADBC9.若为一条直线,为三个互不重合的平面,给出下面三个命题:①;②;③.其中正确的命题有()A.0个B.1个C.2个D.3个10.如图,在正三棱锥P—ABC中,E、F分别是PA、AB的中点,CEF∠=90°,若AB=a,则该三棱锥的全面积为()A.B.C.D.11.如图,正三棱柱的各棱长都为2,分别为AB、A1C1的中点,则EF的长是()(A)2(B)(C)(D)12.若是平面外一点,则下列命题正确的是()(A)过只能作一条直线与平面相交(B)过可作无数条直线与平面垂直(C)过只能作一条直线与平面平行(D)过可作无数条直线与平面平行13.对于任意的直线与平面,在平面内必有直线,使与()(A)平行(B)相交(C)垂直(D)互为异面直线14.对于平面和共面的直线、下列命题中真命题是()(A)若则(B)若则(C)若则(D)若、与所成的角相等,则15.关于直线、与平面、,有下列四个命题:①若,且,则;②若,且,则;③若,且,则;④若,且,则。其中真命题的序号式()A.①②B.③④C.①④D.②③16.给出下列四个命题:①垂直于同一直线的两条直线互相平行②垂直于同一平面的两个平面互相平行③若直线与同一平面所成的角相等,则互相平行④若直线是异面直线,则与都相交的两条直线是异面直线其中假命题的个数是()(A)1(B)2(C)3(D)417.如图平面平面,与两平面、所成的角分别为和。过A、B分别作两平面交线的垂线,垂足为、,若AB=12,则()(A)4(B)6(C)8(D)18.已知正四棱锥SABCD中,23SA,那么当该棱锥的体积最大时,它的高为()A.1B.3C.2D.319.已知三棱锥SABC中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成角的正弦值为()A.34B.54C.74D.3420.有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a的取值范围是()A.(0,62)B.(1,22)C.(62,62)D.(0,22)21.在半径为的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是()A'B'ABA.B.C.D.22.已知,,,SABC是球O表面上的点,SAABC平面,ABBC,1SAAB,2BC,则球O的表面积等于()A.4B.3C.2D.23.将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为()A.B.2+C.4+D.24.如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是()A.点H是△A1BD的垂心B.AH垂直于平面CB1D1C.AH的延长线经过点C1D.直线AH和BB1所成角为45°二、填空题1.多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面内,其余顶点在的同侧,正方体上与顶点A相邻的三个顶点到的距离分别为1,2和4,P是...