高中数学必修2立体几何专题-线面垂直专题典型例题精选精讲VIP免费

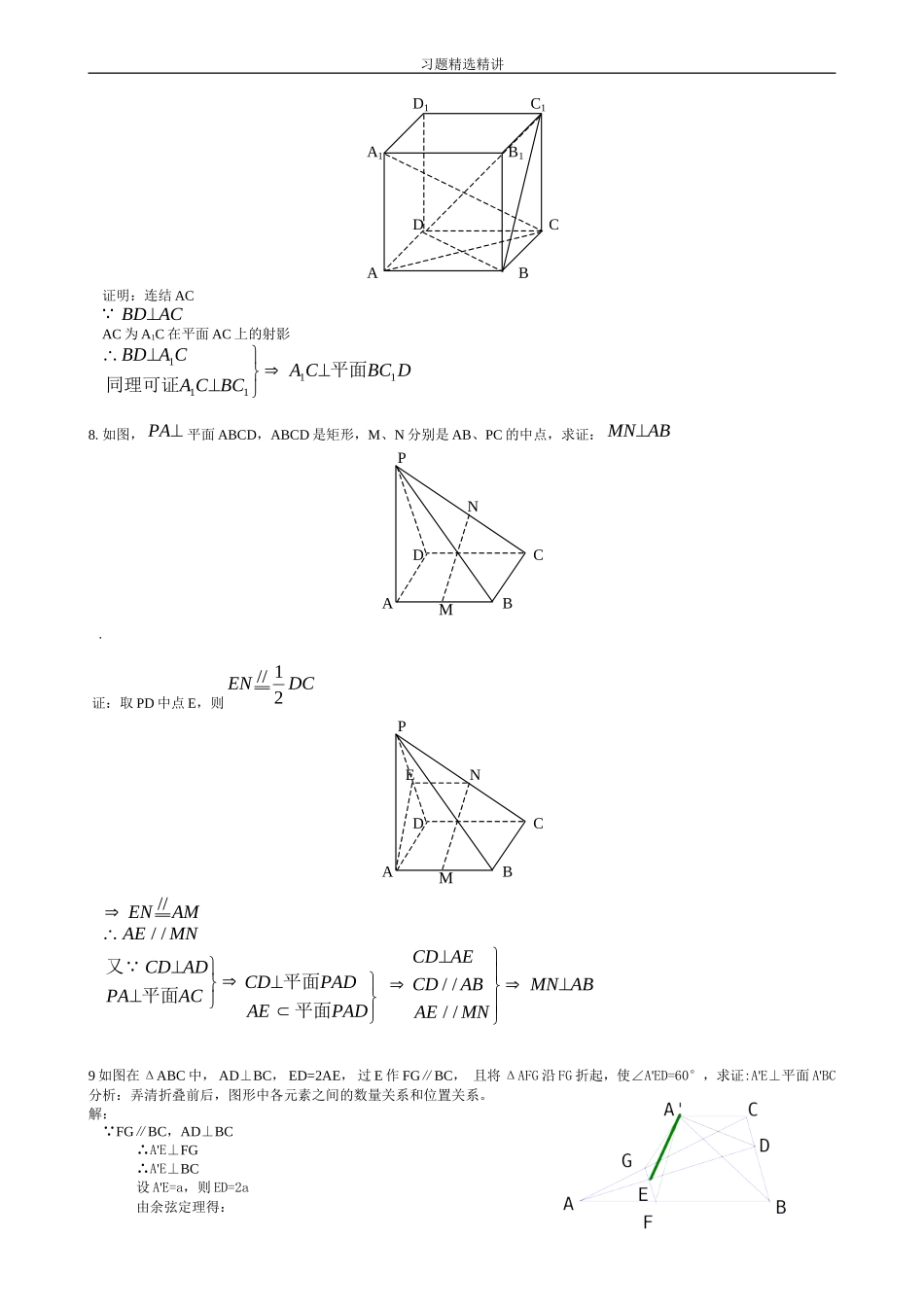
习题精选精讲线面垂直的证明中的找线技巧通过计算，运用勾股定理寻求线线垂直1如图1，在正方体中，为的中点，AC交BD于点O，求证：平面MBD．证明：连结MO，， DB⊥，DB⊥AC，，∴DB⊥平面，而平面∴DB⊥．设正方体棱长为，则，．在Rt△中，． ，∴． OM∩DB=O，∴⊥平面MBD．评注：在证明垂直关系时，有时可以利用棱长、角度大小等数据，通过计算来证明．利用面面垂直寻求线面垂直2如图2，是△ABC所在平面外的一点，且PA⊥平面ABC，平面PAC⊥平面PBC．求证：BC⊥平面PAC．证明：在平面PAC内作AD⊥PC交PC于D．因为平面PAC⊥平面PBC，且两平面交于PC，平面PAC，且AD⊥PC，由面面垂直的性质，得AD⊥平面PBC．又 平面PBC，∴AD⊥BC． PA⊥平面ABC，平面ABC，∴PA⊥BC． AD∩PA=A，∴BC⊥平面PAC．（另外还可证BC分别与相交直线AD，AC垂直，从而得到BC⊥平面PAC）．评注：已知条件是线面垂直和面面垂直，要证明两条直线垂直，应将两条直线中的一条纳入一个平面中，使另一条直线与该平面垂直，即从线面垂直得到线线垂直．在空间图形中，高一级的垂直关系中蕴含着低一级的垂直关系，通过本题可以看到，面面垂直线面垂直线线垂直．一般来说，线线垂直或面面垂直都可转化为线面垂直来分析解决，其关系为：线线垂直线面垂直面面垂直．这三者之间的关系非常密切，可以互相转化，从前面推出后面是判定定理，而从后面推出前面是性质定理．同学们应当学会灵活应用这些定理证明问题．下面举例说明．3如图１所示，ABCD为正方形，⊥平面ABCD，过且垂直于的平面分别交于．求证：，．证明： 平面ABCD，∴． ，∴平面SAB．又 平面SAB，∴． 平面AEFG，∴．∴平面SBC．∴．同理可证．评注：本题欲证线线垂直，可转化为证线面垂直，在线线垂直与线面垂直的转化中，平面起到了关键作用，同学们应多注意考虑线和线所在平面的特征，从而顺利实现证明所需要的转化．习题精选精讲4如图２，在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，作BE⊥CD，Ｅ为垂足，作AH⊥BE于Ｈ．求证：AH⊥平面BCD．证明：取AB的中点Ｆ，连结CF，DF． ，∴． ，∴．又，∴平面CDF． 平面CDF，∴．又，，∴平面ABE，． ，，，∴平面BCD．评注：本题在运用判定定理证明线面垂直时，将问题转化为证明线线垂直；而证明线线垂直时，又转化为证明线面垂直．如此反复，直到证得结论．5如图３，是圆Ｏ的直径，Ｃ是圆周上一点，平面ABC．若AE⊥PC，Ｅ为垂足，Ｆ是PB上任意一点，求证：平面AEF⊥平面PBC．证明： AB是圆Ｏ的直径，∴． 平面ABC，平面ABC，∴．∴平面APC． 平面PBC，∴平面APC⊥平面PBC． AE⊥PC，平面APC∩平面PBC＝PC，∴AE⊥平面PBC． 平面AEF，∴平面AEF⊥平面PBC．评注：证明两个平面垂直时，一般可先从现有的直线中寻找平面的垂线，即证线面垂直，而证线面垂直则需从已知条件出发寻找线线垂直的关系．6.空间四边形ABCD中，若AB⊥CD，BC⊥AD，求证：AC⊥BDADBOC证明：过A作AO⊥平面BCD于O。ABCDCDBO，同理BC⊥DO∴O为△ABC的垂心于是BDCOBDAC7.证明：在正方体ABCD－A1B1C1D1中，A1C⊥平面BC1D习题精选精讲D1C1A1B1DCAB证明：连结ACBDACAC为A1C在平面AC上的射影BDACACBCACBCD11111同理可证平面8.如图，PA平面ABCD，ABCD是矩形，M、N分别是AB、PC的中点，求证：MNABPNDCABM.证：取PD中点E，则ENDC//12PENDCABMENAM//AEMN//又平面平面平面CDADPAACCDPADAEPADCDAECDABAEMNMNAB////9如图在ΔABC中，AD⊥BC，ED=2AE，过E作FG∥BC，且将ΔAFG沿FG折起，使∠A'ED=60°，求证:A'E⊥平面A'BC分析：弄清折叠前后，图形中各元素之间的数量关系和位置关系。解： FG∥BC，AD⊥BC∴A'E⊥FG∴A'E⊥BC设A'E=a，则ED=2a由余弦定理得：习题精选精讲A'D2=A'E2+ED2-2•A'E•EDcos60°=3a2∴ED2=A'D2+A'E2∴A'D⊥A'E∴A'E⊥平面A'BC10如图,在空间四边形SABC中,SA平面ABC,ABC=90,ANSB于N,AMSC于M。求证:①ANBC;②SC平面ANM分析:①要证ANBC,转证,BC平面SAB。②要证SC平面ANM,转证,SC垂直于平面ANM内的两条相交直线,即证SC...