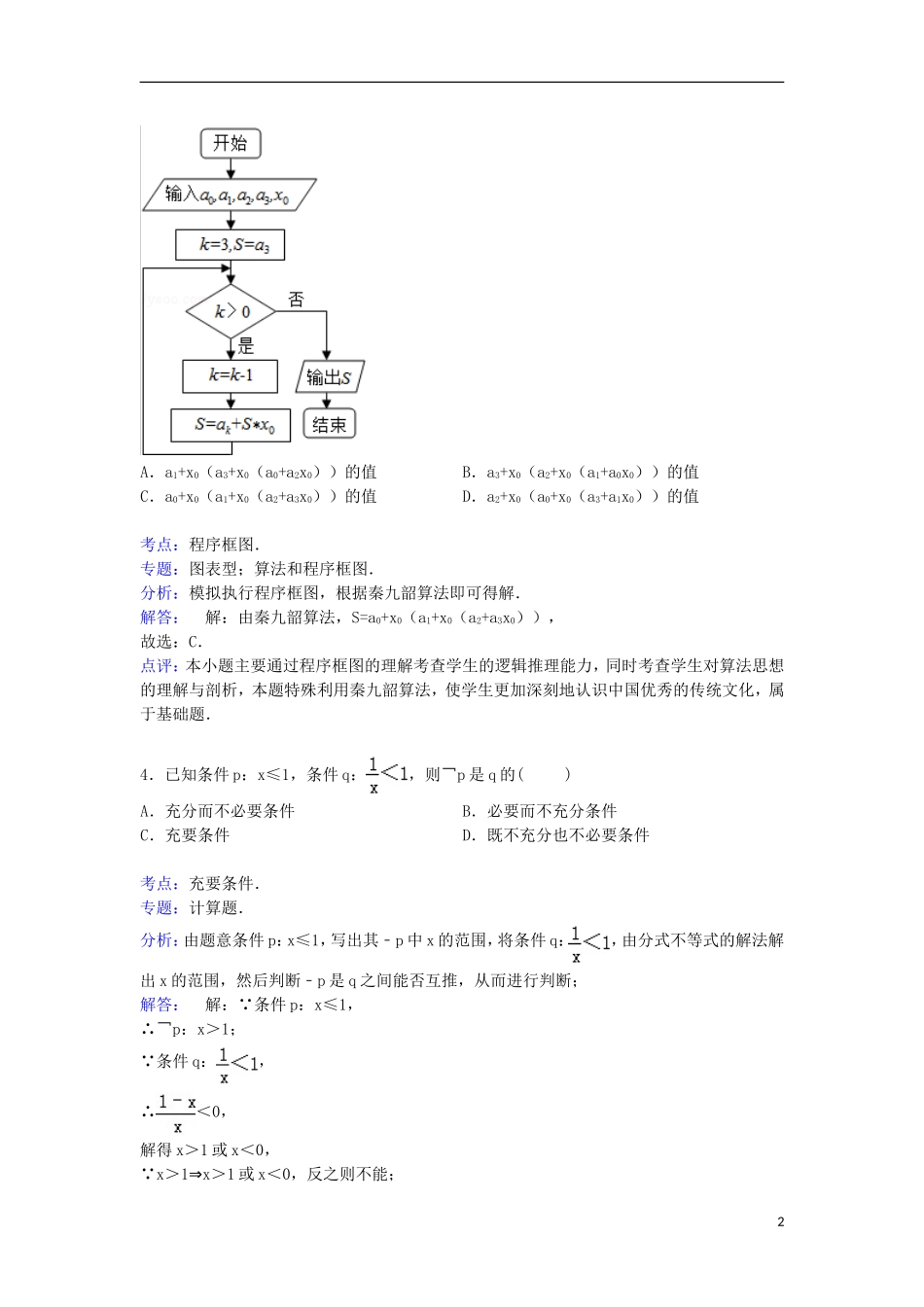
湖北省随州市2014-2015学年高二下学期期末数学试卷(文科)一、选择题(共12小题,每小题5分,满分60分)1.复数z=﹣4i+3的虚部是()A.﹣4iB.3iC.3D.﹣4考点:复数的基本概念.专题:数系的扩充和复数.分析:利用复数的基本概念:复数a+bi的实部为a,虚部为b,解得.解答:解:复数z=﹣4i+3=3+(﹣4)i的虚部是﹣4;故选D.点评:本题考查了复数的基本概念;复数a+bi的实部为a,虚部为b.2.有一段“三段论”推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(x0)=0,所以,x=0是函数f(x)=x3的极值点.以上推理中()A.大前提错误B.小前提错误C.推理形式错误D.结论正确考点:演绎推理的基本方法.专题:计算题;推理和证明.分析:在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不难得到结论.解答:解:大前提是:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不是真命题,因为对于可导函数f(x),如果f'(x0)=0,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误,故选A.点评:本题考查的知识点是演绎推理的基本方法,演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.3.如图是秦九韶算法的一个程序框图,则输出的S为()1A.a1+x0(a3+x0(a0+a2x0))的值B.a3+x0(a2+x0(a1+a0x0))的值C.a0+x0(a1+x0(a2+a3x0))的值D.a2+x0(a0+x0(a3+a1x0))的值考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序框图,根据秦九韶算法即可得解.解答:解:由秦九韶算法,S=a0+x0(a1+x0(a2+a3x0)),故选:C.点评:本小题主要通过程序框图的理解考查学生的逻辑推理能力,同时考查学生对算法思想的理解与剖析,本题特殊利用秦九韶算法,使学生更加深刻地认识中国优秀的传统文化,属于基础题.4.已知条件p:x≤1,条件q:,则¬p是q的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件考点:充要条件.专题:计算题.分析:由题意条件p:x≤1,写出其﹣p中x的范围,将条件q:,由分式不等式的解法解出x的范围,然后判断﹣p是q之间能否互推,从而进行判断;解答:解: 条件p:x≤1,∴¬p:x>1; 条件q:,∴<0,解得x>1或x<0, x>1⇒x>1或x<0,反之则不能;2∴﹣p⇒q,q推不出﹣p,∴﹣p是q的充分而不必要条件,故选A.点评:此题主要考查逻辑关系的条件和分式方程的求解问题,解题时按部就班的求解,此题思路很明显就是求出﹣p和q,各自x的范围.5.用反证法证明命题:“若a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为()A.a,b都能被3整除B.a,b都不能被3整除C.a,b不都能被3整除D.a不能被3整除考点:反证法与放缩法.专题:综合题.分析:“a,b中至少有一个能被3整除”的反面是:“a,b都不能被3整除”,故应假设a,b都不能被3整除.解答:解:反证法证明命题时,应假设命题的反面成立.“a,b中至少有一个能被3整除”的反面是:“a,b都不能被3整除”,故应假设a,b都不能被3整除,故选B.点评:本题考查用反证法证明命题,应假设命题的反面成立.6.已知a<b<|a|,则()A.>B.ab<1C.>1D.a2>b2考点:不等关系与不等式.分析:利用赋值法,排除错误选项,从而确定正确答案.解答:解: a<b<|a|,∴a<0,b的正负不确定;若b=0,可排除A,C;若b=﹣1,a=﹣2,则ab=2>1,故C错误;无论b>0还是b<0,b=0,D均成立.故选D.点评:利用赋值法排除错误选项,可以有效地简化解题过程.7.已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是()cm2.3A.B.C.2D.4考点:由三视图求面积、...