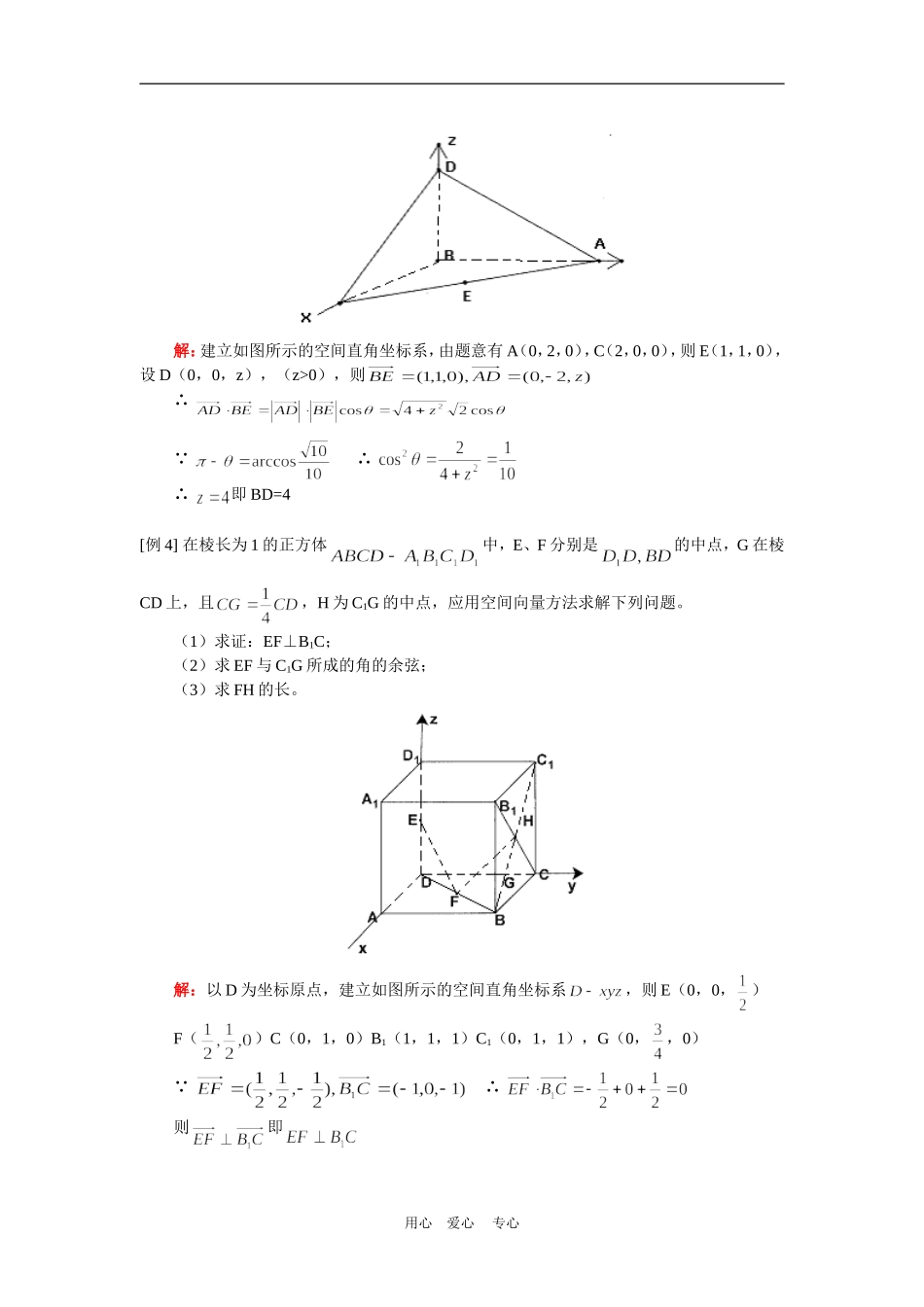
高二数学(理)立体几何中的向量方法人教实验版(A)【本讲教育信息】一.教学内容:立体几何中的向量方法二.重点、难点:直线,m的方向向量为平面的法向量为(1)(2)(3)(4)(5)(6)【典型例题】[例1]已知,若且,求x+y的值。解:由①又即②由①②有:或∴或[例2]设向量,计算,并确定的关系,使与z轴垂直。解:由即当满足即使与z轴垂直[例3]如图,在空间四边形ABCD中,AB、BC、BD两两垂直,且AB=BC=2,E是AC的中点,异面直线AD和BE所成的角为,求BD的长度。用心爱心专心解:建立如图所示的空间直角坐标系,由题意有A(0,2,0),C(2,0,0),则E(1,1,0),设D(0,0,z),(z>0),则∴ ∴∴即BD=4[例4]在棱长为1的正方体中,E、F分别是的中点,G在棱CD上,且,H为C1G的中点,应用空间向量方法求解下列问题。(1)求证:EF⊥B1C;(2)求EF与C1G所成的角的余弦;(3)求FH的长。解:以D为坐标原点,建立如图所示的空间直角坐标系,则E(0,0,)F()C(0,1,0)B1(1,1,1)C1(0,1,1),G(0,,0) ∴则即用心爱心专心(2)∴由(1)知故EF与所成角的余弦值为(3) H为C1G1的中点∴H(0,),又F()∴即[例5]如图,在棱长为2的正方体中,E是DC的中点,取如图所示的空间直角坐标系。(1)写出A、B1、E、D1的坐标;(2)求AB1与D1E所成的角的余弦值。解:(1)A(2,2,0)B1(2,0,2),E(0,1,0),D1(0,2,2)(2) ∴,∴与所成的角的余弦值为[例6]如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中用心爱心专心点。(1)求证:EF//平面PAD;(2)求证:EF⊥CD;(3)若,求EF与平面ABCD所成的角的大小。证:如图,建立空间直角坐标系,设,,则:A(0,0,0),B(),C(),D(),P() E为AB的中点,F为PC的中点∴E(),F()(1) ∴∴与、共面又 平面PAD∴EF//平面PAD(2) ∴∴CD⊥EF(3)若,则有,即∴∴∴ 平面AC∴是平面AC的法向量∴EF与平面AC所成的角为:[例7]在正方体中,如图E、F分别是BB1,CD的中点,(1)求证:平面ADE;(2)用心爱心专心解:建立如图所示的直角坐标系,(1)不妨设正方体的棱长为1,则D(0,0,0),A(1,0,0,),D1(0,0,1),E(1,1,),F(0,,0)则,则∴∴平面ADE(2)B1(1,1,1),C(0,1,0),故∴,则[例8]如图,在四棱锥中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。(1)证明PA//平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C—PB—D的大小。用心爱心专心解:如图所示建立空间直角坐标系,D为坐标原点,设DC=。(1)证明:连结AC,AC交BD于G,连结EG依题意得A(),P(0,0,a),E() 底面ABCD是正方形∴G是此正方形的中心故点G的坐标为()且,∴,这表明PA//EG,而平面EDB且PA平面EDB∴PA//平面EDB(2)证明:依题意得B(),又,故∴PB⊥DE,由已知EF⊥PB,且,所以PB⊥平面EFD(3)解:设点F的坐标为(),,则从而,所以由条件EF⊥PB知,即解得∴点F的坐标为()用心爱心专心且,即,故是二面角C—PB—D的平面角 且∴∴,所以,二面角C—PC—D的大小为[例9]如图,直三棱柱ABC—A1B1C1中,底面是等腰直角三角形,,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是的垂心G。(1)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);(2)求点A1到平面AED的距离。解:(1)连结BG,则BG是BE在面ABD的射影,即是与平面ABD所成的角,如图所示建立坐标系,坐标原点为O,设CA=,则A(),B(),D(0,0,1),A1(,0,2),E(),G()∴∴,解得∴,∴A1B与平面ABD所成角是用心爱心专心(2)由(1)有A(2,0,0),A1(2,0,2),E(1,1,1),D(0,0,1)∴平面AA1E,又ED平面AED∴平面AED⊥平面AA1E,又面AED面AA1E=AE∴点A在平面AED的射影K在AE上设,则由,即,解得∴,即即点A1到平面AED的距离为[例10]如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离。解:如图,设,以为坐标向量建立空间直角坐标系C—xyz由题设C(0,0...