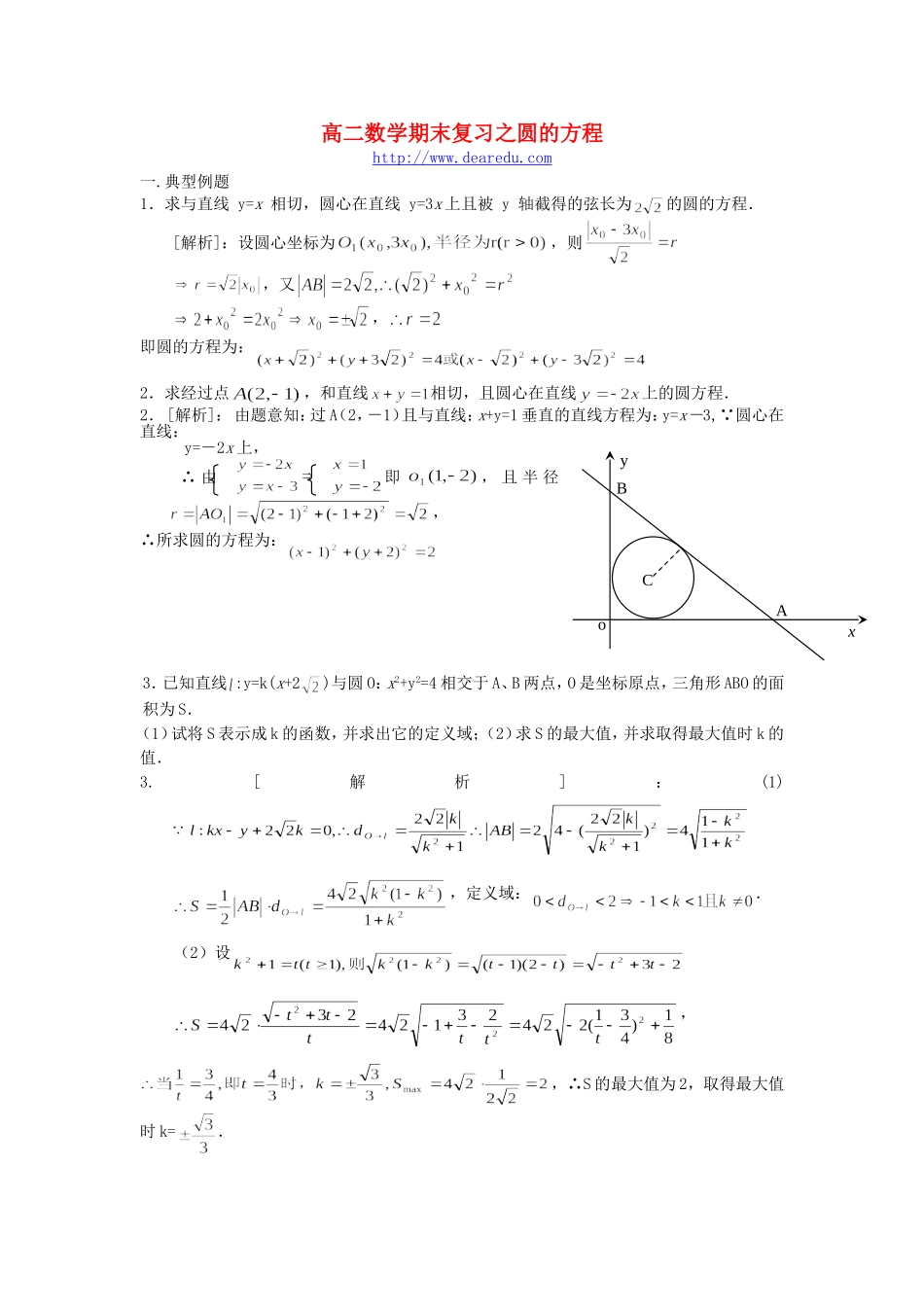
xyoABC高二数学期末复习之圆的方程http://www.dearedu.com一.典型例题1.求与直线y=x相切,圆心在直线y=3x上且被y轴截得的弦长为的圆的方程.[解析]:设圆心坐标为,则,又,即圆的方程为:2.求经过点,和直线相切,且圆心在直线上的圆方程.2.[解析]:由题意知:过A(2,-1)且与直线:x+y=1垂直的直线方程为:y=x-3,∵圆心在直线:y=-2x上,∴由即,且半径,∴所求圆的方程为:3.已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.(1)试将S表示成k的函数,并求出它的定义域;(2)求S的最大值,并求取得最大值时k的值.3.[解析]:(1),定义域:.(2)设,,∴S的最大值为2,取得最大值时k=.4.设圆的方程为,直线的方程为.(1)求关于对称的圆的方程;(2)当变化且时,求证:的圆心在一条定直线上,并求所表示的一系列圆的公切线方程.[解析]:(1)圆C1的圆心为C1(-2,3m+2)设C1关于直线的对称点为C2(a,b)则解得:∴圆C2的方程为(2)由消去m得a-2b+1=0,即圆C2的圆心在定直线:x-2y+1=0上.设直线y=kx+b与圆系中的所有圆都相切,则即∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m值都成立,所以有:,所以所表示的一系列圆的公切线方程为:二.巩固练习(一)、选择题1.原点必位于圆:的(C)A.内部B.圆周上C.外部D.均有可能2.“点M在曲线y=|x|上”是“点M到两坐标轴距离相等”的(C)A.充要条件B.必要不充分条件C.充分不必要条件D.非充分非必要条件3.从动点向圆作切线,其切线长的最小值是(A)A.B.C.D.4.若曲线x2+y2+a2x+(1–a2)y–4=0关于直线y–x=0的对称曲线仍是其本身,则实数a=(B)A.B.C.D.5.圆截直线所得的弦长是(A)A.2B.1C.D.6.若圆与两坐标轴无公共点,那么实数的取值范围是(B)A.B.C.D.7.若直线与曲线有交点,则(C)A.有最大值,最小值B.有最大值,最小值C.有最大值0,最小值D.有最大值0,最小值8.直线y=x+b与曲线x=有且仅有一个公共点,则b的取值范围是(B)A.|b|=B.C.D.以上都错9.圆上到直线3x+4y-11=0的距离等于1的点有(C)A.1个B.2个C.3个D.4个10.直线与圆(θ为参数)的位置关系是(C)A.相离B.相切C.相交但不过圆心D.相交且过圆心11.已知圆C:(a>0,)及直线:,若直线被C截得的弦长为,则=(C)A.B.C.D.12.过两圆:x2+y2+6x+4y=0及x2+y2+4x+2y–4=0的交点的直线的方程(A)A.x+y+2=0B.x+y-2=0C.5x+3y-2=0D.不存在(二)、填空题13.过P(1,2)的直线l把圆分成两个弓形当其中劣孤最短时直线的方程为14.斜率为3,且与圆x2+y2=10相切的直线方程是.15.已知BC是圆的动弦,且|BC|=6,则BC的中点的轨迹方程是______.16.若实数x,y满足的最大值是..