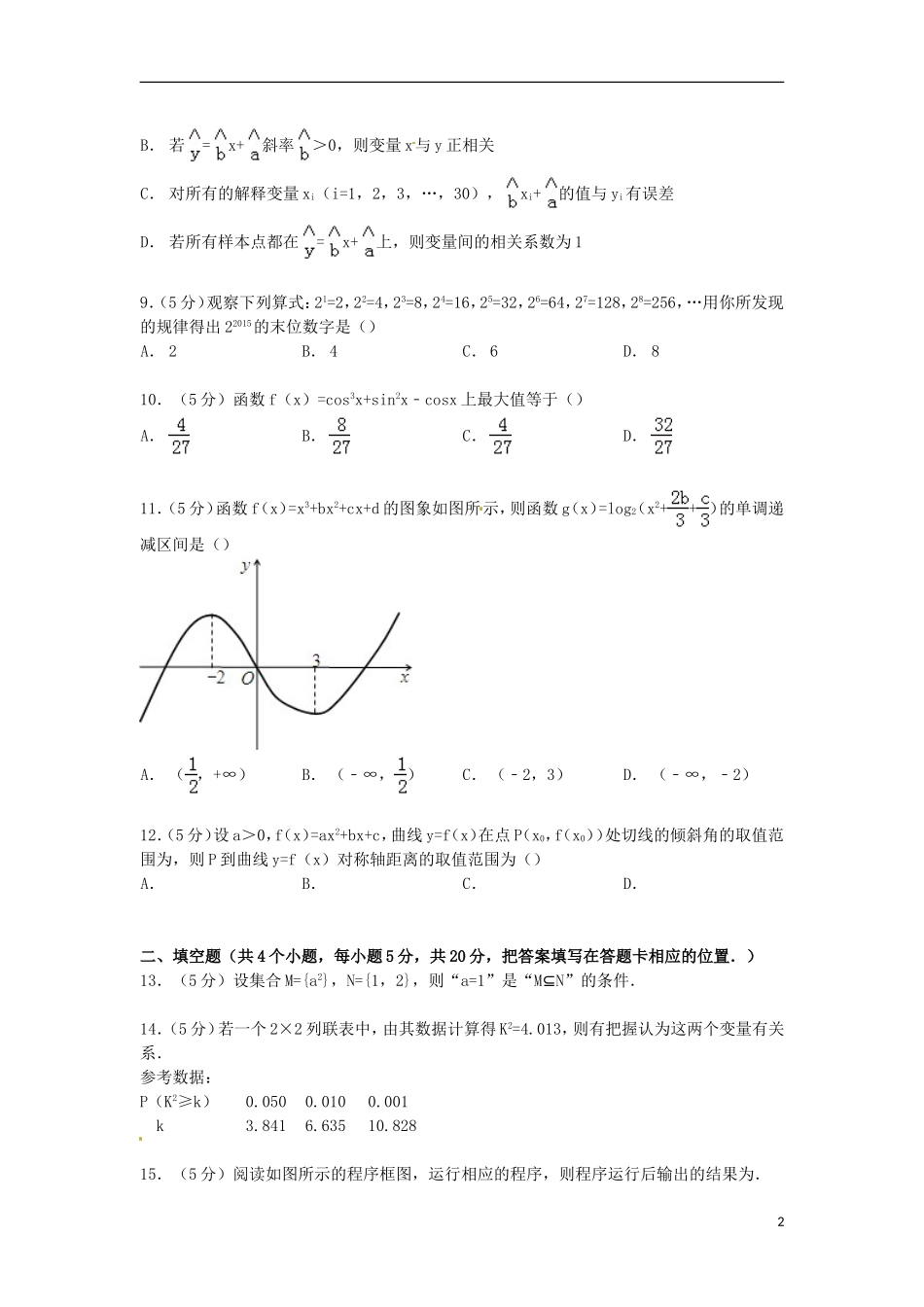
重庆市名校联盟2014-2015学年高二下学期期中数学试卷(文科)一、选择题(共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)复数z=3﹣i的虚部是()A.1B.iC.﹣1D.﹣i2.(5分)“因为指数函数y=ax是增函数(大前提),而y=()x是指数函数(小前提),所以y=()x是增函数(结论)”,上面推理的错误是()A.大前提错导致结论错B.小前提错导致结论错C.推理形式错导致结论错D.大前提和小前提错都导致结论错3.(5分)命题:“方程X2﹣2=0的解是X=”中使用逻辑联系词的情况是()A.没有使用逻辑连接词B.使用了逻辑连接词“且”C.使用了逻辑连接词“或”D.使用了逻辑连接词“非”4.(5分)设i为虚数单位,则复数等于()A.B.C.D.5.(5分)曲线y=x3+x﹣2在点P0处的切线平行于直线y=4x,则点P0的坐标是()A.(0,1)B.(1,0)C.(﹣1,﹣4)或(1,0)D.(﹣1,﹣4)6.(5分)函数f(x)=|x﹣2|﹣lnx的零点个数为()A.0B.1C.2D.37.(5分)定义在闭区间上的连续函数y=f(x)有唯一的极值点x=x0,且y极小值=f(x0),则下列说法正确的是()A.函数f(x)在上不一定有最小值B.函数f(x)在上有最小值,但不一定是f(x0)C.函数f(x)在上有最小值f(x0)D.函数f(x)在上的最大值也可能是f(x0)8.(5分)已知一组样本点(xi,yi),(其中i=1,2,3,…,30),变量x与y线性相关,且根据最小二乘法求得的回归方程是=x+,则下列说法正确的是()A.至少有一个样本点落在回归直线=x+上1B.若=x+斜率>0,则变量x与y正相关C.对所有的解释变量xi(i=1,2,3,…,30),xi+的值与yi有误差D.若所有样本点都在=x+上,则变量间的相关系数为19.(5分)观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…用你所发现的规律得出22015的末位数字是()A.2B.4C.6D.810.(5分)函数f(x)=cos3x+sin2x﹣cosx上最大值等于()A.B.C.D.11.(5分)函数f(x)=x3+bx2+cx+d的图象如图所示,则函数g(x)=log2(x2++)的单调递减区间是()A.(,+∞)B.(﹣∞,)C.(﹣2,3)D.(﹣∞,﹣2)12.(5分)设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为,则P到曲线y=f(x)对称轴距离的取值范围为()A.B.C.D.二、填空题(共4个小题,每小题5分,共20分,把答案填写在答题卡相应的位置.)13.(5分)设集合M={a2},N={1,2},则“a=1”是“M⊆N”的条件.14.(5分)若一个2×2列联表中,由其数据计算得K2=4.013,则有把握认为这两个变量有关系.参考数据:P(K2≥k)0.0500.0100.001k3.8416.63510.82815.(5分)阅读如图所示的程序框图,运行相应的程序,则程序运行后输出的结果为.216.(5分)已知函数y=f(x)是定义在R上的奇函数,且当x<0时,不等式f(x)+xf′(x)<0成立,若a=30.3f(30.3),b=(logπ3)f(logπ3),c=(log3)f(log3),则a,b,c间的大小关系是.三、解答题(共6题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知m∈R,复数z=m(m﹣2)+(m2+2m﹣3)i,(1)m为何值时z为纯虚数?(2)若z对应的点位于复平面第二象限,求m的范围.18.(12分)已知函数f(x)=x3﹣ax2+(a2﹣1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y﹣3=0.(1)求a,b的值;(2)求函数f(x)的单调区间,并求出f(x)在区间上的最大值.19.(12分)下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:x23456y2.23.85.56.57.0y与x之间有较强线性相关性.(1)求线性回归直线方程=x+,(2)试估计使用年限为10年时,维修费用多少万元?参考公式:=,=﹣.20.(12分)某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为t元(t为常数,且2≤t≤5),设该食品厂每公斤蘑菇的出厂价为x元(25≤x≤40),根据市场调查,销售量q与ex成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.(Ⅰ)求该工厂的每日利润y元与每公斤蘑菇...