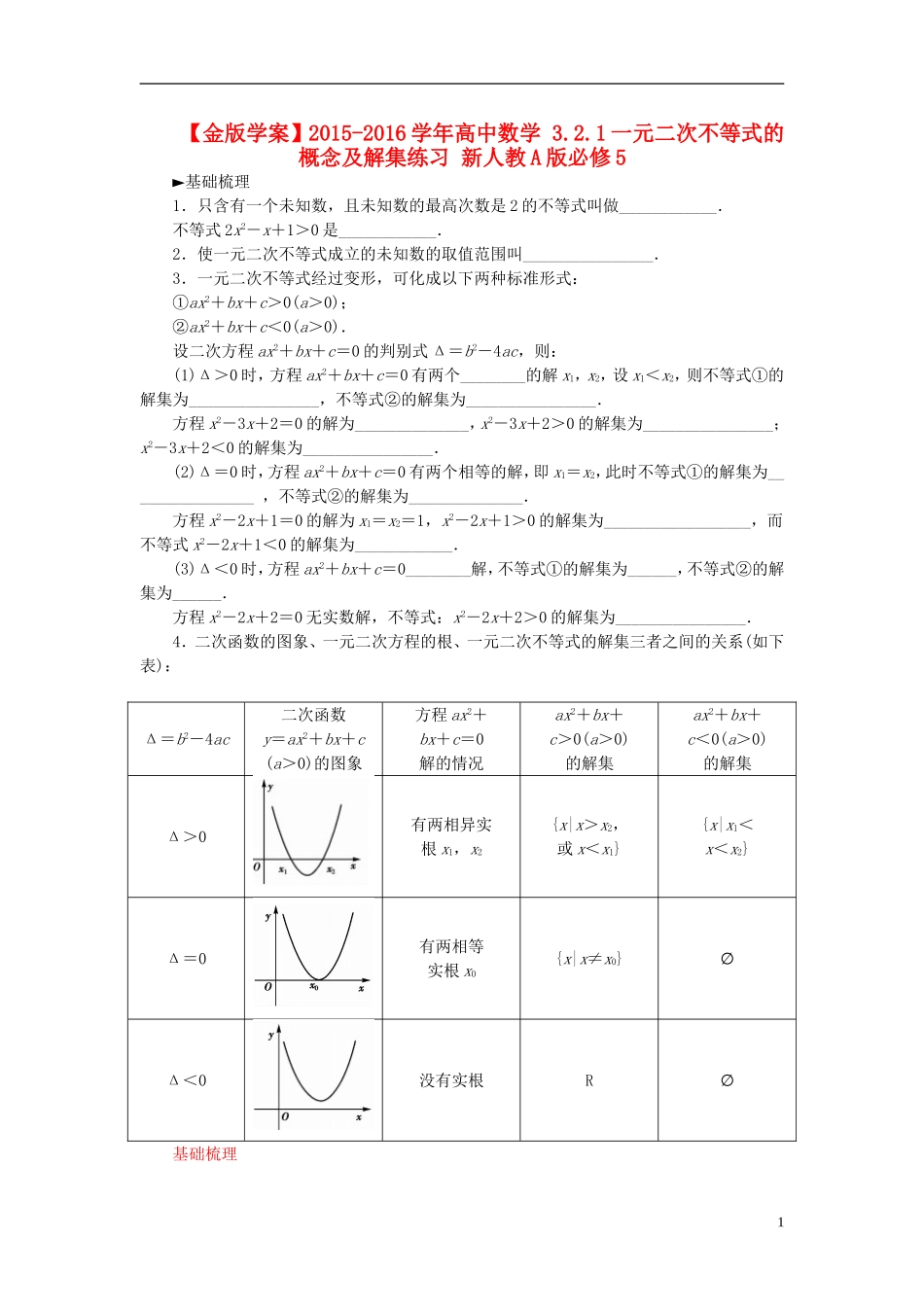
【金版学案】2015-2016学年高中数学3.2.1一元二次不等式的概念及解集练习新人教A版必修5►基础梳理1.只含有一个未知数,且未知数的最高次数是2的不等式叫做____________.不等式2x2-x+1>0是____________.2.使一元二次不等式成立的未知数的取值范围叫________________.3.一元二次不等式经过变形,可化成以下两种标准形式:①ax2+bx+c>0(a>0);②ax2+bx+c<0(a>0).设二次方程ax2+bx+c=0的判别式Δ=b2-4ac,则:(1)Δ>0时,方程ax2+bx+c=0有两个________的解x1,x2,设x1<x2,则不等式①的解集为________________,不等式②的解集为________________.方程x2-3x+2=0的解为______________,x2-3x+2>0的解集为________________;x2-3x+2<0的解集为________________.(2)Δ=0时,方程ax2+bx+c=0有两个相等的解,即x1=x2,此时不等式①的解集为________________,不等式②的解集为______________.方程x2-2x+1=0的解为x1=x2=1,x2-2x+1>0的解集为__________________,而不等式x2-2x+1<0的解集为____________.(3)Δ<0时,方程ax2+bx+c=0________解,不等式①的解集为______,不等式②的解集为______.方程x2-2x+2=0无实数解,不等式:x2-2x+2>0的解集为________________.4.二次函数的图象、一元二次方程的根、一元二次不等式的解集三者之间的关系(如下表):Δ=b2-4ac二次函数y=ax2+bx+c(a>0)的图象方程ax2+bx+c=0解的情况ax2+bx+c>0(a>0)的解集ax2+bx+c<0(a>0)的解集Δ>0有两相异实根x1,x2{x|x>x2,或x<x1}{x|x1<x<x2}Δ=0有两相等实根x0{x|x≠x0}∅Δ<0没有实根R∅基础梳理11.一元二次不等式一元二次不等式2.一元二次不等式的解集3.(1)不相等x1=1,x2=2{x|x>2或x<1}{x|1<x<2}(2){x|x∈R且x≠x1}∅{x|x∈R且x≠1}∅(3)无实数R∅R►自测自评1.不等式(x+2)(3-x)>0的解集是()A.{x|x>3或x<-2}B.{x|-3<x<2}C.{x|x>2或x<-3}D.{x|-2<x<3}2.不等式-6x2-x+2≤0的解集是()A.B.C.D.3.(2013·广东卷)不等式x2+x-2<0的解集为________.自测自评1.D2.解析:由已知可得6x2+x-2≥0,即(2x-1)(3x+2)≥0,∴x≥或x≤-.答案:B3.(-2,1)►基础达标1.已知集合A={x|x2-x-2<0},B={x|-10C.x2+6x+10>0D.2x2-3x+4<07.解析:利用“Δ”判断,在不等式x2+6x+10>0中,Δ=62-40<0,∴不等式x2+6x+10=0的解集为R,故选C.答案:C8.不等式x(3-x)≥x(x+2)+1的解集是________.8.解析:由x(3-x)≥x(x+2)+1⇒2x2-x+1≤0. Δ=(-1)2-4×2×1<0,∴方程2x2-x+1=0无实根,结合y=2x2-x+1的图象得原不等式的解集为∅.答案:∅9.解下列不等式:(1)4x2+4x+1>0;(2...