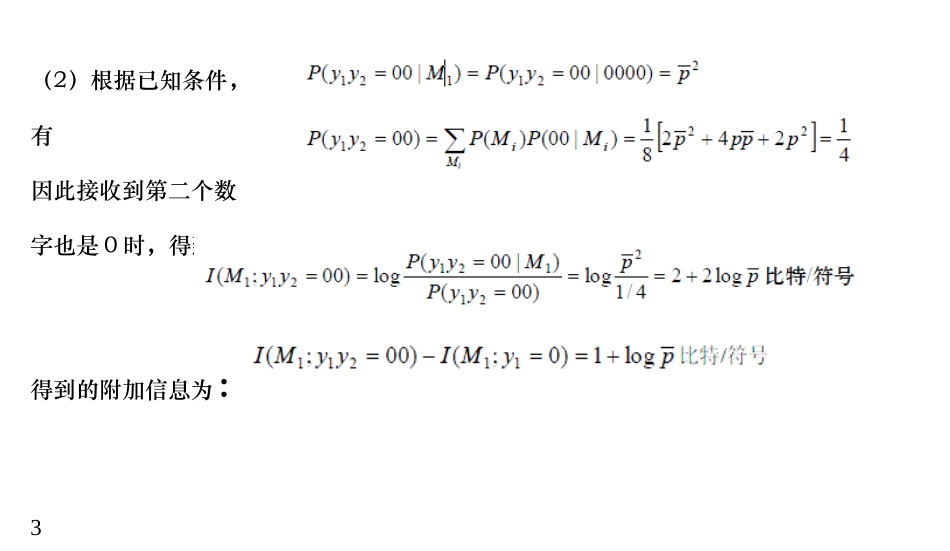【3.2】设8个等概率分布的消息通过传递概率为p的BSC进行传送,8个消息相应编成下述码字:M1=0000,M2=0101,M3=0110,M4=0011M5=1001,M6=1010,M7=1100,M8=1111试问:(1)接收到第一个数字0与M1之间的互信息;(2)接收到第二个数字也是0时,得到多少关于M1的附加互信息;(3)接收到第三个数字仍为0时,又增加了多少关于M1的互信息;1(4)接收到第四个数字还是0时,再增加了多少关于M1的互信息。解:各个符号的先验概率均为1/8(1)根据已知条件,有因此接收到第一个数字0与M1之间的互信息为:2(2)根据已知条件,有因此接收到第二个数字也是0时,得到多少关于M1的互信息为:得到的附加信息为:3(3)根据已知条件,有因此接收到第三个数字也是0时,得到多少关于M1的互信息为:4此时得到的附加信息为:(4)根据已知条件,有因此接收到第四个符号为0时,得到的关于M1的互信息为5此时得到的附加信息为6【3.3】设二元对称信道的传递矩阵为(1)若P(0)=3/4,P(1)=1/4,求H(X),H(X|Y),H(Y|X)和I(X;Y);(2)求该信道的信道容量及其达到信道容量时的输入概率分布。解:(1)根据已知条件,有789【3.5】若X、Y和Z是三个随机变量,试证明:(1)I(X;YZ)=I(X;Y)+I(X;Z|Y)=I(X;Z)+I(X;Y|Z)(2)I(X;Y|Z)=I(Y;X|Z)=H(X|Z)-H(X|YZ)(3)I(X;Y|Z)³0当且仅当(X,Z,Y)是马氏链时等式成立。1011(3)1213【3.10】求下列两个信道的信道容量,并加以比较1415因此有161718【4.17】在图片传输中,每帧约个像素,为了能很好地重现图像,需分16个亮度电平,并假设亮度电平等概率分布。试计算每秒钟传送30帧图片所需信道的带宽(信噪功率比为30dB)。解:每秒需要传输的信息量为:19【4.18】设在平均功率受限高斯加性波形信道中,信道带宽为3kHz,又设(信号功率+噪声功率)/噪声功率=10dB。(1)试计算该信道传送的最大信息率(单位时间);(2)若功率信噪比降为5dB,要达到相同的最大信息传输率,信道带宽应为多少?解:(1)根据已知条件有,20(2)如果功率信噪比降为5dB,即因此2122解:23【5.2】有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F。24(1)求这些码中哪些是惟一可译码;(2)求哪些码是非延长码(即时码);(3)求对所有惟一可译码求出其平均码长L。解:(1)上述码字中,A为等长码,且为非奇异码,因此码A为惟一可译码;码B中,根据惟一可译码的判断方法,可求得其尾随后缀集合为{1,11,111,1111,11111},且其中任何后缀均不为码字,因此码B是惟一可译码。码C为逗点码,因此码C为惟一可译码;码D不是惟一可译码,因为其尾随后缀集合中包含0,而0又是码字;码E的尾随后缀集合为空集,因此码E是惟一可25译码;码F不是惟一可译码,因为其尾随后缀集合中包含0,而0又是码字,因此F不是惟一可译码。(2)码A、C、E是即时码(非延长码)(3)码A的平均码长为3;码B的平均码长为2.125;码C的平均码长为2.125;码F的平均码长为2。26【5.3】证明定理5.6,若存在一个码长为l1,l2,,lq的惟一可译码,则一定存在具有相同码长的即时码。如果存在码长为的惟一可译码,则必定满足如下不等式而如果码长满足上述不等式,根据Kraft不等式构造即时码的方法,可27以构造出码长为的即时码,具体构造过程略,参照课本相关定理。28【5.5】若有一信源每秒钟发出2.66个信源符号。将此信源的输出符号送入某一个二元信道中进行传输(假设信道是无噪无损的),而信道每秒钟只传递两个二元符号。试问信源不通过编码能否直接与信道连接?若通过适当编码能否中在信道中进行无失真传输?若能连接,试说明如何编码并说明原因。解:如果不通过编码,即信道的两个码符号对应两个信源符号,而信道传输码符号的速度小于信源发出信源符号的速度,因此势必会造成信源符号的堆积,因此不通过编码是无法将信源与信道直接连接。信源平均每秒发出的信息量为29而该信道的信道容量为1比特/符号,平均每秒能够传输的最大信息量为2比特,因此通过编码可以实现二者的连接。若要连接,需要对扩展信源的信源符号进行编码,目的是使送入信道的信息量小于信道每秒能接收的最大信息量(或使...