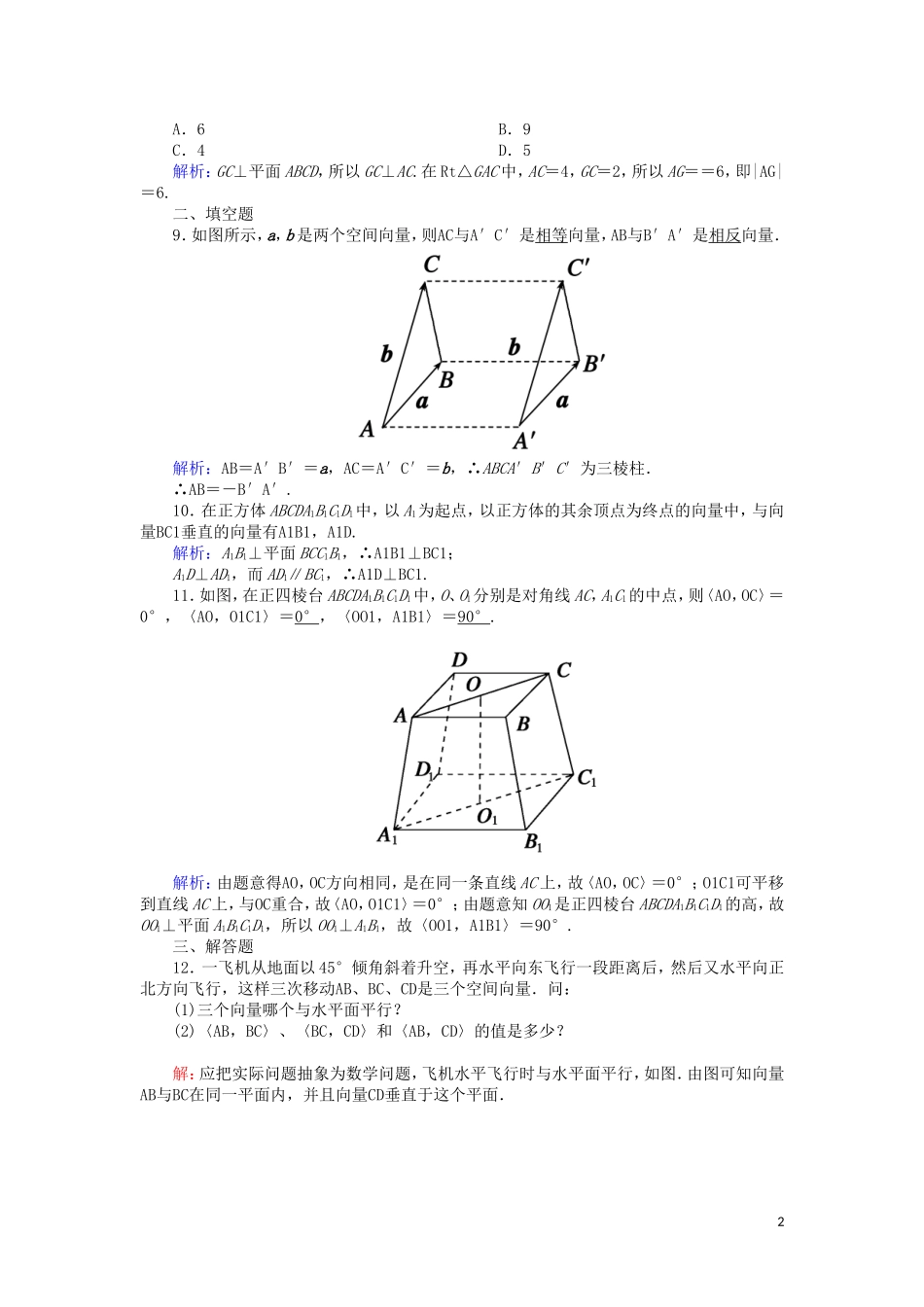
课时作业5从平面向量到空间向量时间:45分钟——基础巩固类——一、选择题1.下列说法中正确的是(D)A.两个有共同起点且相等的向量,其终点可能不同B.若非零向量AB和CD是共线向量,则A,B,C,D四点共线C.在空间中,任意两个单位向量都相等D.零向量与任意向量平行解析:A项错,因为两个向量起点相同,且是相等的向量,所以终点必相同;B项错,若AB和CD共线,则AB和CD的基线平行或重合,所以A,B,C,D不一定在同一条直线上;C项错,单位向量的模相等,但方向不一定相同;D显然正确.2.对于空间任意两个非零向量a,b,a∥b是〈a,b〉=0的(B)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:显然,〈a,b〉=0⇒a∥b.a∥b包括向量a,b同向共线和反向共线两种情形(即当a∥b时,〈a,b〉=0或π),因此a∥b⇒〈a,b〉=0.故a∥b是〈a,b〉=0的必要不充分条件.3.在平行六面体ABCDA1B1C1D1中,下列说法正确的是(C)A.AA1是平面ABCD的法向量B.AD1=C1BC.〈AB,C1D1〉=πD.AD与B1C1不是共面向量解析:AB∥C1D1,且向量AB与向量C1D1方向相反,∴〈AB,C1D1〉=π.4.在四边形ABCD中,若AB=DC,且|AC|=|BD|,则四边形ABCD为(B)A.菱形B.矩形C.正方形D.不确定解析:若AB=DC,则AB=DC,且AB∥DC,∴四边形ABCD为平行四边形,又|AC|=|BD|,即AC=BD,∴四边形ABCD为矩形.5.在棱长为1的正方体ABCDA1B1C1D1中,M和N分别为A1B1和BB1的中点,那么与直线AM垂直的向量有(D)A.CNB.BCC.CC1D.B1C1解析:由于所求的是向量,所以首先排除B,在剩下的三个选项中,通过正方体的图形可知D项正确.6.在平行六面体ABCDA1B1C1D1中,向量D1A、D1C、A1C1是(C)A.有相同起点的向量B.等长向量C.共面向量D.不共面向量解析:先画出平行六面体的图像(图略),可看出向量D1A、D1C在平面ACD1上,由于向量A1C1平行于AC,所以向量A1C1经过平移可以移到平面ACD1上,因此向量D1A、D1C、A1C1为共面向量.7.空间中,起点相同的所有单位向量的终点构成的图形是(D)A.圆B.球C.正方形D.球面解析:根据模的概念知终点在以起点为球心,半径为1的球面上.8.已知正方形ABCD的边长为4,GC⊥平面ABCD,且GC=2,则向量AG的模为(A)1A.6B.9C.4D.5解析:GC⊥平面ABCD,所以GC⊥AC.在Rt△GAC中,AC=4,GC=2,所以AG==6,即|AG|=6.二、填空题9.如图所示,a,b是两个空间向量,则AC与A′C′是相等向量,AB与B′A′是相反向量.解析:AB=A′B′=a,AC=A′C′=b,∴ABCA′B′C′为三棱柱.∴AB=-B′A′.10.在正方体ABCDA1B1C1D1中,以A1为起点,以正方体的其余顶点为终点的向量中,与向量BC1垂直的向量有A1B1,A1D.解析:A1B1⊥平面BCC1B1,∴A1B1⊥BC1;A1D⊥AD1,而AD1∥BC1,∴A1D⊥BC1.11.如图,在正四棱台ABCDA1B1C1D1中,O、O1分别是对角线AC,A1C1的中点,则〈AO,OC〉=0°,〈AO,O1C1〉=0°,〈OO1,A1B1〉=90°.解析:由题意得AO,OC方向相同,是在同一条直线AC上,故〈AO,OC〉=0°;O1C1可平移到直线AC上,与OC重合,故〈AO,O1C1〉=0°;由题意知OO1是正四棱台ABCDA1B1C1D1的高,故OO1⊥平面A1B1C1D1,所以OO1⊥A1B1,故〈OO1,A1B1〉=90°.三、解答题12.一飞机从地面以45°倾角斜着升空,再水平向东飞行一段距离后,然后又水平向正北方向飞行,这样三次移动AB、BC、CD是三个空间向量.问:(1)三个向量哪个与水平面平行?(2)〈AB,BC〉、〈BC,CD〉和〈AB,CD〉的值是多少?解:应把实际问题抽象为数学问题,飞机水平飞行时与水平面平行,如图.由图可知向量AB与BC在同一平面内,并且向量CD垂直于这个平面.2(1)飞机水平飞行时所经过的路线与水平面平行,因而三个向量中BC和CD平行于水平面α.(2)由于向量AB与BC在同一平面内,设为平面β,又由于CD为正北方向,所以CD垂直于平面β,即BC⊥CD和AB⊥CD.因为AB与水平面的夹角为45°,所以得:〈AB,BC〉=45°,〈BC,CD〉=90°,〈AB,CD〉=90°.13.如图所示,长方体ABCDA1B1C1D1,AB=3,AD=2,AA1=1,在以长方体的八个顶点为始点和终点的向量中:(1)单位向量共有多少个?(2)试写出模为的所有...