力学竞赛辅导VIP免费

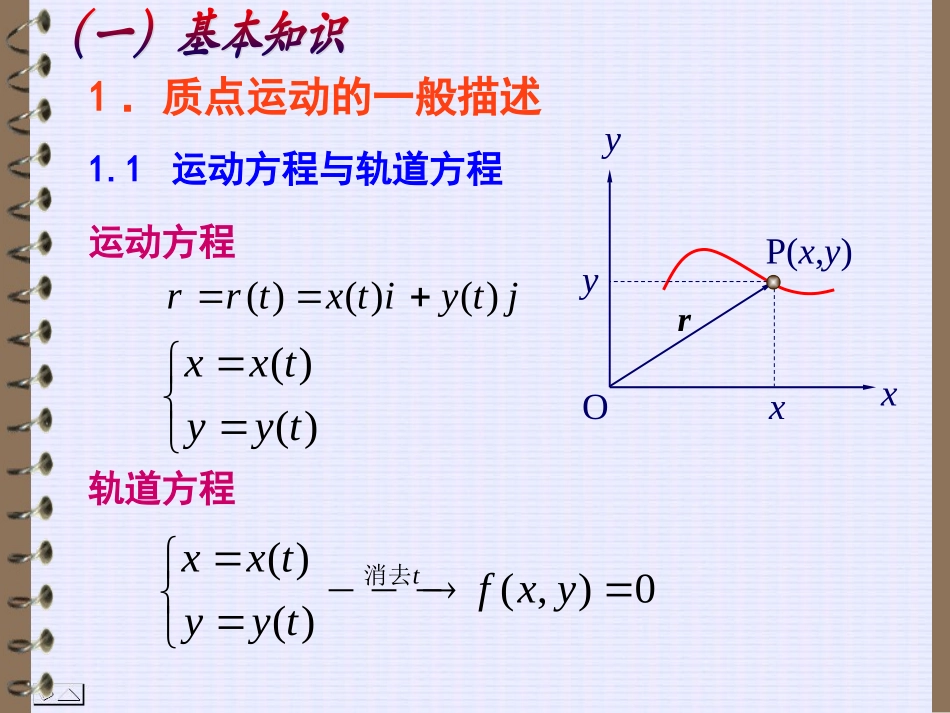
一.质点运动学二.静力学三.牛顿运动定律四.动量与能量五.角动量定理角动量守恒定律六.万有引力与天体运动七.简谐振动1．质点运动的一般描述1.1运动方程与轨道方程轨道方程运动方程()(,)0()txxtfxyyyt消去()()()rrtxtiytjrP(x,y)xOyxy()()xxtyyt1.2速度反映质点运动的快慢和方向的物理量rvtdtrdtrvtlim0dtdyvdtdxvyx瞬时速度沿轨道切线方向yxOBArrArB1.3加速度反映速度（大小和方向）变化快慢的物理量加速度与速度的方向一般不同。vat220limdtrddtvdtvatxOzyvAvvBABrArBvAvB(a)(b)2222dtyddtdvadtxddtdvayyxxgyv0Ox2.抛体运动速度：00cossinxyvvvvgt运动方程：020cos1sin2xvtyvtgt轨道方程：2220tan2cosgyxxv推论1）飞行时间：02sinvTg2）上升高度：220maxsin2vHyg3）射程：20sin2vsggyv0Ox思考甲、乙两小孩在做游戏，甲在树上，乙在地上用枪描准甲，乙一开枪，甲就从树上跳下（初速度为零）。问：甲是否被击中？若被击中，求出被击中的时间和地点。甲乙0vsh3.1圆周运动的加速度00naaan22tannnaaaaaRPxOP0s0n0avaan3.圆周运动2ndvadtvaR3.2圆周运动的角量描述角位置：=(t)角速度:dtdttlim0角加速度:dtdttlim03.3角量和线量的关系Rv2naRaRRPxOP0s0rrr0vvvaaa0xySOPSOxyrrr04.相对运动4.1运动描述与参照系：对物体运动的描述与参照系有关——位移、速度、加速度的测量与参照系有关。4.2不同参照系间位移、速度和加速度的变换绝对速度=牵连速度+相对速度22tannnaaaaa2::ndvadtva切向加速度法向加速度00naaanaana1.一般曲线运动1.1一般曲线运动中的加速度1.2曲率半径的物理求法椭圆的曲率半径：AByxOab22221xyab轨道方程：cossinxatybt对应运动方程：A点：22nnvvaa2,max,max,ynxvvbaaa22Anvbaa2Bab同理：抛物线的曲率半径：yxOyvvxvnaaa2yAx轨道方程：0212xvtyat对应运动方程：2223/22222223/23/200400()(14)(1)2nvatvvaxAxaavavA202aAv其中：022220xyvvvvatvat02220cosnavaavat2.连体运动问题解题方法一：运动的分解情形1：两物体通过刚性细杆或不可伸长的绳子相连，他们在连线方向的位移、速度和加速度相等。v2v112coscosvv情形2：两刚性物体接触点的速度沿法向分量相等。12coscosvvv1v2情形3：两直线相交点的运动等于各直线沿对方直线方向运动的合运动：12PvvvPv1v2v11vv22v1212,,sinsinvvvv2212122cosPvvvvv22121212cossinvvvv例1.1如图，一人拉着绳子的一端在水平面上以速度0v匀速前进。求当绳子与水平面夹角为时，重物上升的速度。hv0v0v||||0cosvvv解：Pv0vP例1.2如图示，一半径为R的半圆柱体沿水平方向以速度v0作匀速运动。求杆与半圆柱体的接触点P的角位置为时竖直杆运动的速度。0sincosPvv解：0tanPvvRO例1.3水平直杆AB在半径为R的固定圆圈上以匀速v0竖直下落，如图所示，试求套在该直线和圆圈的交点处小环M的速度。OMRv0v0v2v1v0解：01sinMvvvA对B：ABABABrva、、解题方法二：运动的合成（相对运动）一个物体同时参与两种运动实质上是参照系的转换：BBBrva、、B对地：AABBAABBAABABrrrvvvaaa、、A对地：例1.4如图，缠在线轴上的绳子一头搭在墙上的光滑钉子A上。今以恒定速度v拉绳，当绳与竖直...