第四章-直梁的弯曲4VIP免费

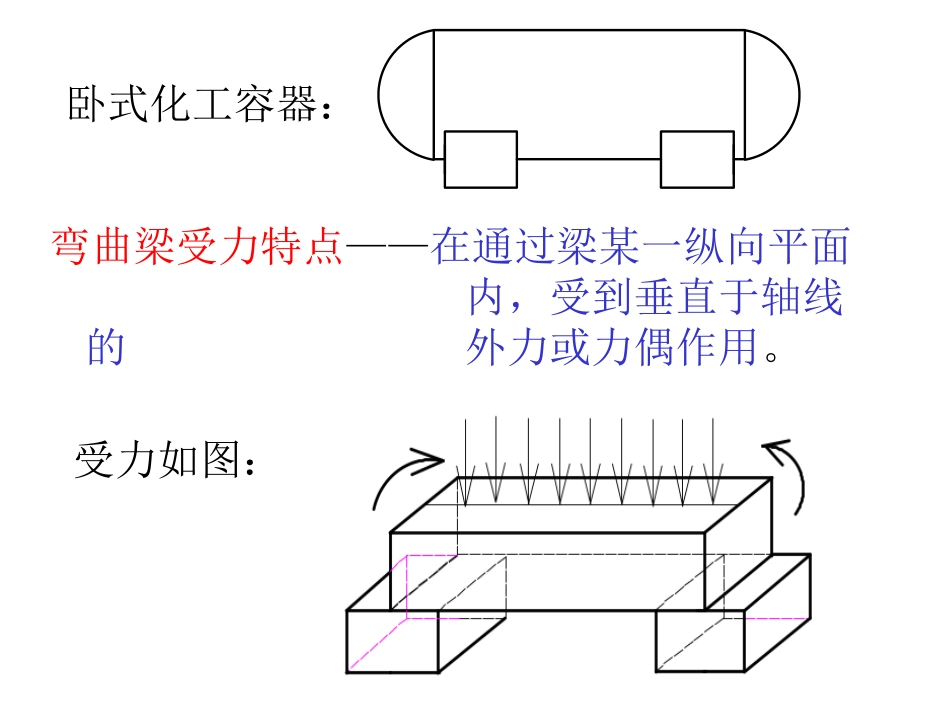
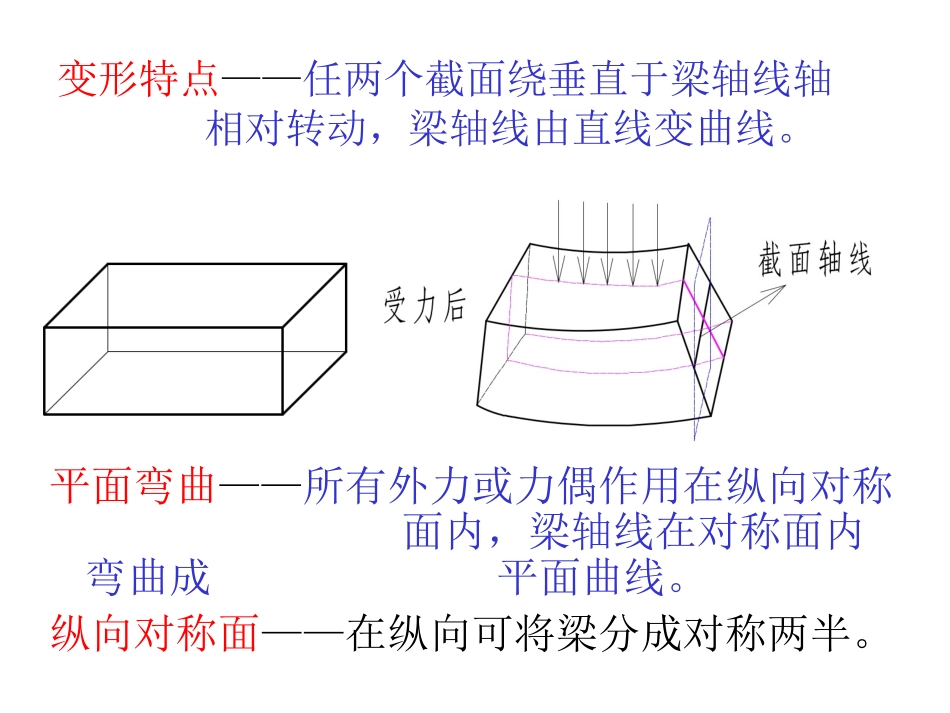
第四章直梁的弯曲4§4-1平面弯曲概念梁的类型1、梁弯曲常见弯曲变形构件,如房屋支承梁，工厂中起重机横梁及化工中的卧式容器等。结构如图：卧式化工容器：弯曲梁受力特点——在通过梁某一纵向平面内，受到垂直于轴线的外力或力偶作用。受力如图：变形特点——任两个截面绕垂直于梁轴线轴相对转动，梁轴线由直线变曲线。平面弯曲——所有外力或力偶作用在纵向对称面内，梁轴线在对称面内弯曲成平面曲线。纵向对称面——在纵向可将梁分成对称两半。2、梁简化对实际梁受力分析和强度计算，对梁进行简化，以轴线表示梁。梁简化成三种力学模型：（1）简支梁如图：一端固定简支，另一端可动铰支。（2）外伸梁如图：梁一端或两端伸出支座外。（3）悬臂梁如图：梁一端固定约束，另一端自由。各支座处力与位移边界条件：①固定铰支支座处梁左、右，上、下均不可移动，但可绕约束点转动。解除约束受力图RRxy力的边界条件位移边界条件m=0Rx≠0Ry≠0x=0y=0②可动铰支支座点左、右可移动，上、下不可动。解除约束受力图Ry力的边界条件位移边界条件Ry≠0Rx=0m=0x≠0y=0③固定端约束限制固定端既不能转动，也不可移动。解除约束受力图RyRxm力的边界条件位移边界条件Rx≠0Ry≠0m≠0x=0y=0各支座反力可根据平衡条件求出。如果未知力数与所列出的独立方程数相同，则可求出未知力——称为静定问题，属于静定梁；反之为静不定，称为不静定梁或超静定问题。①集中力：作用力作用在很小面积上，可近似一点。如图：②集中力偶：力偶两力分布在很短一段梁上，可简化为作用在梁的某一截面上。如图：③分布载荷：载荷分布在较长范围内，以单位长度受力q表示。q单位N/m如图：作用于梁上载荷有三种形式：Pmq§4-2梁弯曲时的内力一、内力计算内力计算方法如下：第一步——解除支座约束，计算约束反力。第二步——用截面法将梁分成两部分。第三步——由平衡条件计算截面处内力。如图：简支梁，试计算m—n截面内力。解:(1)解除约束，求约束反力列平衡方程nABabmPRRRxAyAyBRxA=0RyA+RyB=PRyB·(a+b)–Pa=0baPaRyBbaPbRyA0xAR(2)用截面法求内力MMQQxoPRAyRBy截面处存在的内力：①阻止RyA作用下绕O转动，截面必存在附加内力矩M，阻止转动。②平衡RyA力，截面上必有向下力Q附加内力矩M——称为截面弯矩。截面内力Q——称为剪力，与外力平行，有使梁沿m—n截面剪断趋势。分离体处于平衡，由平衡条件得：∑y=0RAy–Q=0∑M=0M–RAy·x=0baPbQxbaPbM结论：①受弯曲梁任一截面内力有弯矩与剪力。②剪力等于截面之左（或右）所有外力代数和。③弯矩等于截面之左（或右）所有外力（力偶）对截面形心之矩代数和。剪力与弯矩对梁强度影响：由经典力学分析弯矩对梁强度影响远大于剪力对梁强度。工程计算一般只考虑弯矩，忽略剪力。二、弯矩符号规定规定如下：所求弯矩的截面附近能形成上凹下凸的弯曲变形，该截面弯矩为正；反之为负。m—n截面附近弯曲形状，如图，弯矩M为正。反之发生如下图弯曲形状，弯矩为负。MmnMmnMM由此得“左顺右逆”弯矩为正规定：截面左侧——所有对截面形心之矩为顺时针的外力及顺时针的力偶，它们在截面处产生弯矩为正，反之为负。截面右侧——所有对截面形心之矩为逆时针的外力及逆时针的力偶，它们在截面处产生弯矩为正，反之为负。§4-3弯矩图由截面法计算出横截面弯矩随轴线x变化规律M=M(x)→称为梁弯矩方程将弯矩大小与正负表示在图上——弯矩图画弯矩图的基本方法：(1)对双支点梁解除约束，求支座反力，悬臂梁不必求支座反力,从悬臂端开始计算。(2)在有集中力或集中力偶处分段，求出每一段弯矩方程。(3)选适当比例，以横截面位置x为横坐标，弯矩M为纵坐标作弯矩图。例一，如图：受集中载荷简支梁。试画出弯矩图。解：①解除约束，求约束反力ABCDPmaaaPRRRAxAyBym=PaRAy·3a–P·2a+m=0RAy+RBy–P=03PRAy32PRBy0AxR②分段求各段弯矩AC段，在AC段任取一截面xPxRMAyAC30≤x≤aDC段，在DC段任取一截面)(axPxRMAyDCxPPaPaPxxP323a≤x＜2aPMxRAyxRAyBD段，在BD段任取一截面MRxByPxxRMByBD320≤x＜a③画弯矩图(+)(-)(+)3Pa2Pa3aP3CADB例二、有一...