2.1.1空间点,直线,平面之间的位置关系--平面(1)VIP免费

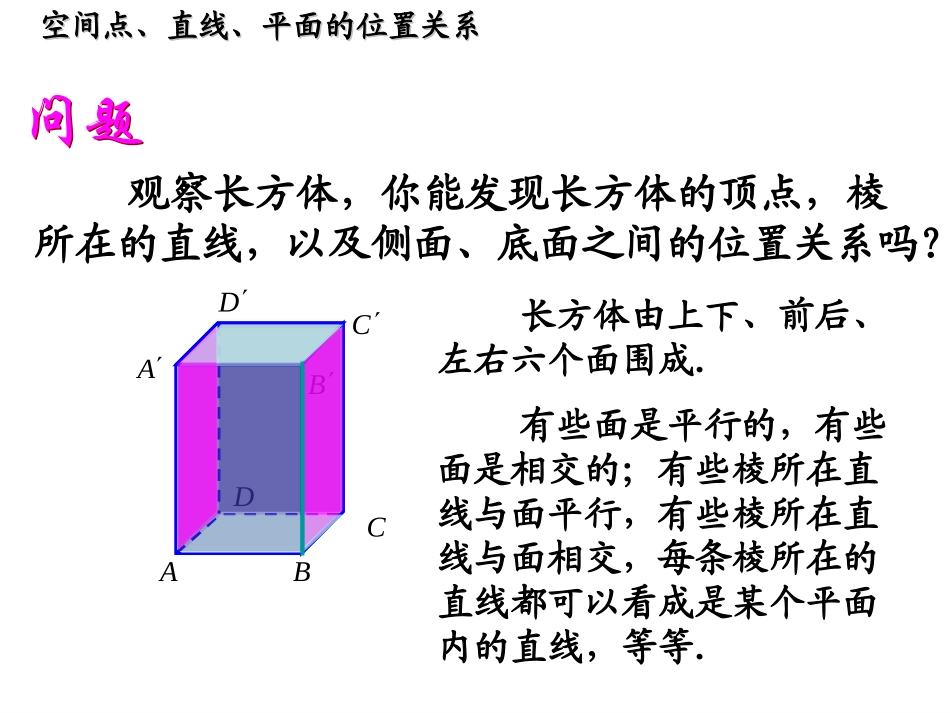
2.1.12.1.1平面平面观察长方体，你能发现长方体的顶点，棱所在的直线，以及侧面、底面之间的位置关系吗？ABABCDCD空间点、直线、平面的位置关系空间点、直线、平面的位置关系长方体由上下、前后、左右六个面围成．有些面是平行的，有些面是相交的；有些棱所在直线与面平行，有些棱所在直线与面相交，每条棱所在的直线都可以看成是某个平面内的直线，等等．观察教室里的桌面、黑板面，它们呈现出怎样的形象？实例引入实例引入观察活动室里的地面，它呈现出怎样的形象？实例引入实例引入观察海面，它又呈现出怎样的形象？实例引入实例引入生活中的一些物体通常呈平面形，课桌面、黑板面、海面都给我们以平面的形象．引入新课引入新课几何里所说的“平面”（plane）就是从这样的一些物体中抽象出来的，但是，几何里的平面是无限延展的．11、平面的概念、平面的概念桌面桌面黑板面黑板面平静的水面平静的水面平面的形象平面的形象几何里的平面是无限延展的.请你从适当的角度和距离观察教室里的桌面、黑板面或门的表面，它们呈现出怎样的形象？2.2.平面的画法平面的画法2.2.平面的画法平面的画法我们常常把水平的平面画成一个平行四边形，用平行四边形表示平面．平行四边形的锐角通常画成45°，且横边长等于其邻边长的2倍．DCABADCBEF被遮挡部分用虚线表示为了增强立体感，常常把被遮挡部分用虚线画出来．2.2.平面的画法平面的画法1、判断下列各题的说法正确与否，在正确的说法的题号后打√，否则打x:1、一个平面长4米，宽2米；()2、平面有边界；()3、一个平面的面积是25cm2；()4、菱形的面积是4cm2；()5、一个平面可以把空间分成两部分.()练习2、图中平面α与平面β是否为同一平面？αβαβαβ不是是不是练习注意：1、平面的两个特征：②平的（没有厚度）①无限延展一个平面把空间分成两部分.2、一条直线把平面分成两部分.DCAB平面ABCD平面AC或平面BDADCBEF平面记作：3.3.平面的表示平面的表示平面记作：平面EF常把希腊字母α、β、γ等写在代表平面的平行四边形的一个角上，如平面α、平面β等；也可以用代表平面的四边形的四个顶点，或者相对的两个顶点的大写英文字母作为这个平面的名称．图形符号语言文字语言(读法)AaAaAaAaAAAAbaAabA点A在直线a上点A不在直线a上点A在平面α内点A不在平面α内直线a、b交于点A4、点、线、面的基本位置关系（1）符号表示：（2）集合关系：点A、线a、面α图形符号语言文字语言(读法)aa直线a在平面内aa直线a与平面无公共点aAaA直线a与平面交于点Al平面与相交于直线l例1.将下列符号语言转化为图形语言：ABAlBl（1）ab//acbcpc（2）(1)BA(2)P说明：画图的顺序:先画大件(平面),再画小件(点、线),,,,,,,(2)直线a经过平面外一点M(3)直线在平面内,又在平面内(1)点A在平面内，但不在平面内例2.将下列文字语言转化为符号语言：l12,(3),,AaabbMNcMNmllP练习：用符号表示下列语句，并画出相应的图形（）点在直线上，直线在平面内（）平面过直线及直线外一点，点在平面外，直线过点平面过平行直线平面过直线和平面外一点如果直线l与平面α有一个公共点P，直线l是否在平面α内？5.5.平面公理平面公理实际生活中，我们有这样的经验：把一根直尺边缘上的任意两点放到桌面上，可以看到，直尺的整个边缘就落在了桌面上．平面公理平面公理如果直线l与平面α有两个公共点，直线l是否在平面α内？公理1如果一条直线上的两点在一个平面内，那么这条直线在此平面内．ABlAlBllAB作用：判定直线是否在平面内．平面公理平面公理在生产、生活中，人们经过长期观察与实践，总结出关于平面的一些基本性质，我们把它作为公理．这些公理是进一步推理的基础．AllAl点A在直线l上．点A在直线l外．AllAlA直线l在平面外．l直线l在平面内．平面经过直线l．l图形、文字、符号图形、文字、符号几种情况？ABl生活中经常看到用三角架支撑照相机．平面公理平面公理平...