材料力学--弯曲应力VIP免费

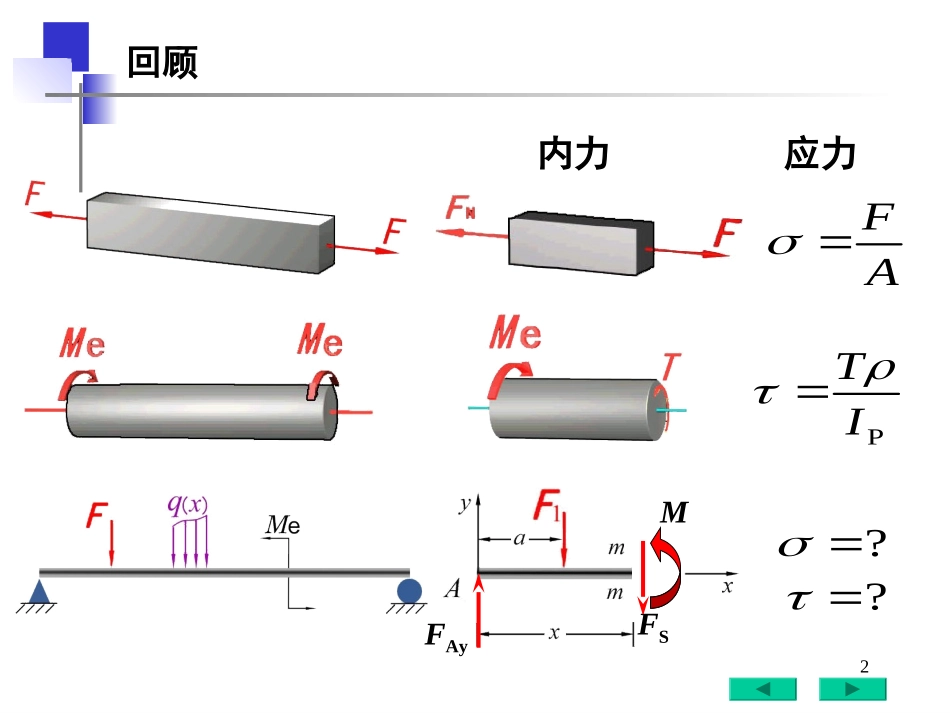
1第五章弯曲应力2回顾内力AF应力PITFAyFSM??3纯弯曲梁段CD上，只有弯矩，没有剪力－－纯弯曲梁段AC和BD上，既有弯矩，又有剪力－－横力弯曲§5.1纯弯曲4弯曲变形实验现象§5.1纯弯曲5平面假设：横截面变形后保持为平面，只是绕截面内某一轴线偏转了一个角度。§5.1纯弯曲6凹入一侧纤维缩短突出一侧纤维伸长中间一层纤维长度不变－－中性层中间层与横截面的交线－－中性轴§5.1纯弯曲7§5.2纯弯曲时的正应力一、变形几何关系8E二、物理关系:yE问题:中性层(y的起点)在哪里？怎样算?1时当pxzyy可确定横截面上的应力分布§5.2纯弯曲时的正应力9平衡条件找答案;0Y;0xm自动满足0X中性轴通过形心(yz为形心主惯性轴)三、平衡条件：yEExzydAAdAAydAE0zSEAdAyEdA;0ZM0E0AySCz0Cy§5.2纯弯曲时的正应力10yIMzMmzMIEdAyEdAyzAA2ZEIM1yEE注意事项：M，y与都有正负号．通常用其绝对值代入公式，用变形确定正应力的正负（拉、压）。正应力分布图ZIMyM最终内力合成0ym0zyAAIEdAyzEdAz惯性矩:zI11主要公式:变形几何关系物理关系yEyE静力学关系Z1EIMZIMy为梁弯曲变形后的曲率1为曲率半径§5.2纯弯曲时的正应力12弯曲正应力公式适用范围弯曲正应力ZIMy•细长梁的纯弯曲或横力弯曲(近似使用)•横截面惯性积Iyz=0•弹性变形阶段)(p§5.2纯弯曲时的正应力13§5.3横力弯曲的正应力纯弯曲正应力ZIMy弹性力学精确分析表明，当跨度l与横截面高度h之比l/h>5（细长梁）时，纯弯曲正应力公式对于横力弯曲近似成立。ZIyMmaxmaxmax横力弯曲最大正应力14弯曲正应力强度条件σσmaxmaxWMIyMzmaxmax1.弯矩最大的截面上2.离中性轴最远处2.脆性材料抗拉和抗压性能不同，二方面都要考虑ttmax,ccmax,注意:1.变截面梁要综合考虑与MzI强度条件maxZZyIW在maxσ抗弯截面系数15常见截面的IZ和WZ圆截面矩形截面空心圆截面空心矩形截面AdAyI2ZmaxZZyIW644ZdI323ZdW)1(6444ZDI)1(3243ZDW123ZbhI62ZbhW12123300ZbhhbI)2//()1212(03300ZhbhhbW16aaFFy解:NmFaM90018.01053竖放时4335412603012cmbhIZ求:(1)截面竖放时距离中性层20mm处的正应力和最大正应力max;(2)截面横放时的最大正应力maxMPayIMmmyZ3.33:20MPayIMZ50105403.09008maxmax横放时4335.1312306012cmhbIZ8maxmax105.13015.0900yIMZmax2100MPa例图示简支梁已知:a=180mm,F=5kN,截面为bh=3060mm2的矩形hb20例题17FFAYAYFFBYBYBAl=3mq=60kN/mxC1mMxm67.5kN8/2ql30zy180120K1.C截面上K点正应力2.C截面上最大正应力3.全梁上最大正应力FSx90kN90kNmkN605.0160190CM1.求支反力kN90AyFkN90ByF4533Zm10832.51218.012.012bhIMPa7.61Pa107.6110832.510)302180(10606533ZKCKIyM（压应力）解：例题已知:E=200GPa,4.C截面的曲率半径ρ1830zy180120KBAl=3mFFAYAYq=60kN/mFFBYBYxC1mMxm67.5kN8/2qlFSx90kN90kN2.C截面最大正应力C截面弯矩mkN60CMC截面惯性矩45Zm10832.5IMPa55.92Pa1055.9210832.510218010606533ZmaxmaxIyMCC例题19BAl=3mFFAYAYq=60kN/mFFBYBYxC1mMxm67.5kN8/2ql30zy180120KFSx90kN90kN3.全梁最大正应力最大弯矩mkN5.67maxM截面惯性矩45m10832.5zIMPa17.104Pa1017.10410832.5102180105.676533ZmaxmaxmaxIyM例题20BAl=3mFFAYAYq=60kN/mFFBYBYxC1mMxm67.5kN8/2ql30zy180120KFSx90kN90kN4.C截面曲率半径ρC截面弯矩mkN60CMC截面惯性矩45Zm10832.5Im4.194106010832.510200359CZCMEIEIM1例题21...