材料力学第四章弯曲应力VIP免费

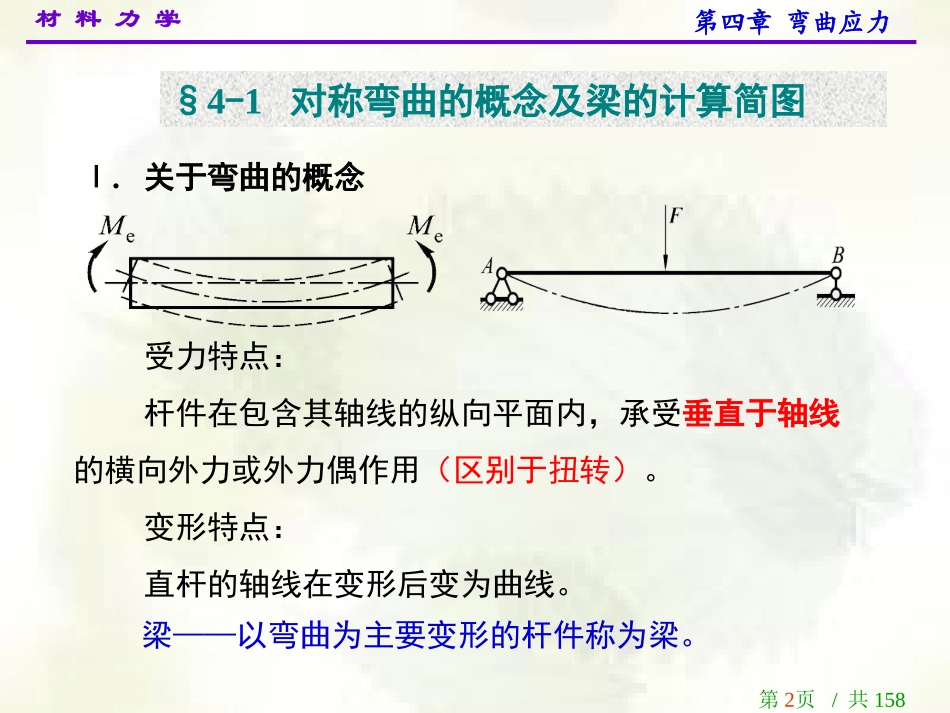
材料力学第1页/共158页第四章弯曲应力§4-1对称弯曲的概念及梁的计算简图§4-2梁的剪力和弯矩·剪力图和弯矩图§4-3平面刚架和曲杆的内力图§4-4梁横截面上的正应力·梁的正应力强度条件§4-5梁横截面上的切应力·梁的切应力强度条件§4-6梁的合理设计材料力学第2页/共158页§4-1对称弯曲的概念及梁的计算简图Ⅰ.关于弯曲的概念受力特点：杆件在包含其轴线的纵向平面内，承受垂直于轴线的横向外力或外力偶作用（区别于扭转）。变形特点：直杆的轴线在变形后变为曲线。梁——以弯曲为主要变形的杆件称为梁。第四章弯曲应力材料力学第3页/共158页弯曲变形第四章弯曲应力材料力学第4页/共158页第四章弯曲应力工程实例F2F1材料力学第5页/共158页纵向对称面对称弯曲——外力作用于梁的纵向对称面内，因而变形后梁的轴线(挠曲线)是在该纵向对称面内的平面曲线。非对称弯曲——梁不具有纵对称面(例如Z形截面梁)，因而挠曲线无与它对称的纵向平面；或梁虽有纵对称面但外力并不作用在纵对称面内，从而挠曲线不与梁的纵对称面一致。第四章弯曲应力材料力学第6页/共158页Ⅱ.梁的计算简图对于对称弯曲的直梁，在计算简图中通常用梁的轴线来代表梁。第四章弯曲应力材料力学第7页/共158页(1)支座的三种基本形式1.固定端——实例如图a，计算简图如图b,c。第四章弯曲应力(b)(c)MRFRxFRy(a)材料力学第8页/共158页2.固定铰支座——实例如图中左边的支座，计算简图如图b，e。3.可动铰支座——实例如图a中右边的支座，计算简图如图c，f。第四章弯曲应力材料力学第9页/共158页悬臂梁(2)梁的三种基本形式简支梁外伸梁第四章弯曲应力材料力学第11页/共158页§4-2梁的剪力和弯矩·剪力图和弯矩图Ⅰ.梁的剪力和弯矩(shearingforceandbendingmoment)图a所示跨度为l的简支梁其约束力为lFaFlalFFBA,梁的左段内任一横截面m－m上的内力，由m－m左边分离体(图b)的平衡条件可知：xlalFxFMlalFFFAA,S第四章弯曲应力截面法材料力学第12页/共158页它们的指向和转向如图b中所示。显然这些内力是m－m右边的梁段对于左边梁段的作用力和作用力矩。故根据作用与反作用原理，m－m左边的梁段对于右边梁段(图c)的作用力和作用力矩数值应与上式所示相同，但指向和转向相反。这一点也可由m－m右边分离体的平衡条件加以检验：第四章弯曲应力材料力学第13页/共158页0,0SByFFFF00xlFxaFMMBClalFlFaFFFFBS从而有xlalFxllFaxaFxlFxaFMB从而有第四章弯曲应力材料力学第14页/共158页梁的横截面上位于横截面内的内力FS是与横截面左右两侧的两段梁在与梁轴相垂直方向的错动(剪切)相对应，故称为剪力；梁的横截面上作用在纵向平面内的内力偶矩是与梁的弯曲相对应，故称为弯矩。第四章弯曲应力材料力学第15页/共158页为使无论取横截面左边或右边为分离体，求得同一横截面上的剪力和弯矩其正负号相同，剪力和弯矩的正负号要以其所在横截面处梁的微段的变形情况确定，如图。第四章弯曲应力剪力正负号：dx微段，左端向上右端向下时，为正。反之为负。弯矩正负号：dx微段下凸为正，即下半部纵向受拉。反之为负。材料力学第18页/共158页Ⅱ.剪力方程和弯矩方程·剪力图和弯矩图剪力方程和弯矩方程实际上是表示梁的横截面上的剪力和弯矩随截面位置变化的函数式，它们分别表示剪力和弯矩随截面位置的变化规律。显示这种变化规律的图形则分别称为剪力图和弯矩图。第四章弯曲应力剪力方程和弯矩方程（表示沿梁各横截面上剪力和弯矩的变化规律）xMMxFFsSS材料力学第19页/共158页例题4-1（补充）图a所示悬臂梁受集度为q的满布均布荷载作用。试作梁的剪力图和弯矩图。第四章弯曲应力(a)材料力学第20页/共158页距右端为x的任意横截面上的剪力FS(x)和弯矩M(x)，根据截面右侧梁段上的荷载有lxqxxqxxMlxqxxF02202S解：1.列剪力方程和弯矩方程当求悬臂梁横截面上的内力(剪力和弯矩)时，若取包含自由端截面的一侧梁段来计算，则可不求出约束力。第四章弯曲应力xMFS(x)材料...