材料力学作业参考题解(2)VIP免费

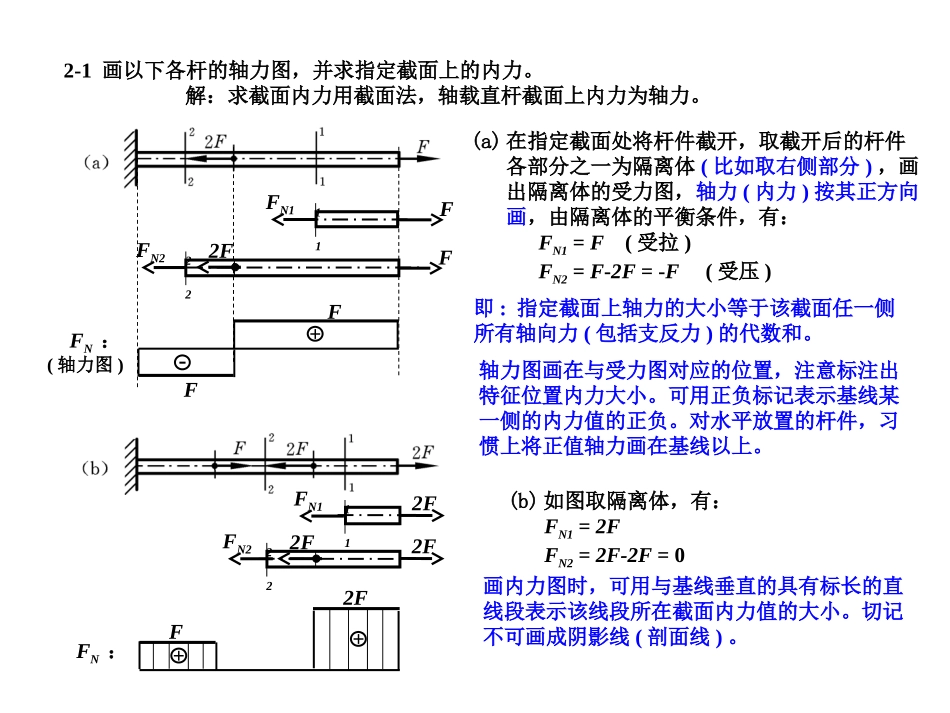
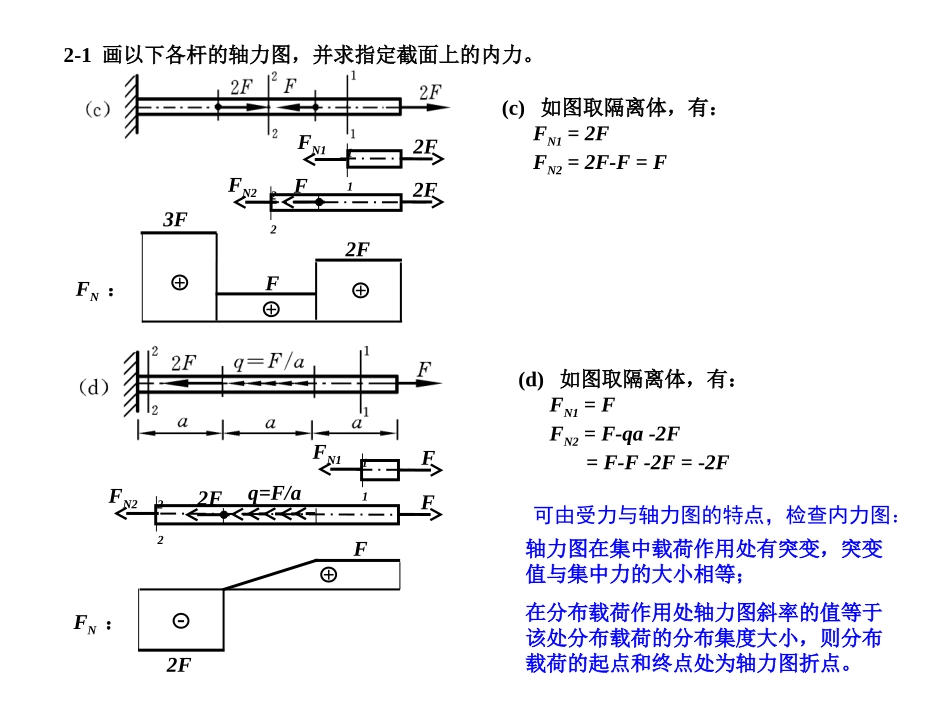
FFFN1FN2F2F1122FF+-FN：(轴力图)2-1画以下各杆的轴力图，并求指定截面上的内力。解：求截面内力用截面法，轴载直杆截面上内力为轴力。(a)在指定截面处将杆件截开，取截开后的杆件各部分之一为隔离体(比如取右侧部分)，画出隔离体的受力图，轴力(内力)按其正方向画，由隔离体的平衡条件，有：FN1=F(受拉)FN2=F-2F=-F(受压)112FFN1222F2FFN2FN：轴力图画在与受力图对应的位置，注意标注出特征位置内力大小。可用正负标记表示基线某一侧的内力值的正负。对水平放置的杆件，习惯上将正值轴力画在基线以上。即:指定截面上轴力的大小等于该截面任一侧所有轴向力(包括支反力)的代数和。(b)如图取隔离体，有：FN1=2FFN2=2F-2F=02F++画内力图时，可用与基线垂直的具有标长的直线段表示该线段所在截面内力值的大小。切记不可画成阴影线(剖面线)。2-1画以下各杆的轴力图，并求指定截面上的内力。(c)如图取隔离体，有：FN1=2FFN2=2F-F=F(d)如图取隔离体，有：FN1=FFN2=F-qa-2F=F-F-2F=-2F112FFN122F2FFN2+FFN：2F++3F11FFN1q=F/a2F22FFN22F-FFN：+轴力图在集中载荷作用处有突变，突变值与集中力的大小相等；在分布载荷作用处轴力图斜率的值等于该处分布载荷的分布集度大小，则分布载荷的起点和终点处为轴力图折点。可由受力与轴力图的特点，检查内力图：2-2图示杆件由两根木杆粘接而成。欲使其在受拉时，粘接面上的正应力为其切应力的2倍，试问粘接面的位置应如何确定？解：本题实质上是要考察斜截面上的应力。由斜截面应力公式，有：2sin2cos2由题义，要求：2则有：21tan2sin22cos2即粘接面法向的角度为：6.2621tan12-4图示实心圆钢杆AB和AC在A点作用有铅垂向下的力F=35kN。已知杆AB和AC的直径分别为d1=12mm和d2=15mm，钢的弹性模量E=210GPa。试求A点在铅垂方向的位移。解：求各杆内力，如图取A点为对象，由平衡条件，有：NABNACNACNABxFFFFF230sin45sin0求位移，各杆变形与A点位移之间的几何关系如图：mmEAlFlACACNACAC104.14/015.0102106.110622.25293求各杆变形(伸长)：AFFNABFNACxykNFkNFFFFFFNACNABNACNABy622.25117.1831230cos45cos0(拉)(拉)mmEAlFlABABNABAB078.14/012.010210210117.18293AAlAAAAlAAABAC45cos45tan30tan30cos有mmllAAABACAy366.130tan130tan45cos30cos整理得45Axy30ABlAClAA2-5图示为打入土中的混凝土地桩，顶端承受载荷F，并由作用于地桩的摩擦力所支持。设沿地桩单位长度的摩擦力为f，且f=ky2，式中，k为常数。试求地桩的缩短量δ。已知地桩的横截面面积为A，弹性模量为E，埋入土中的长度为l。解：地桩所受外载为轴载，且在F和摩擦力共同作用下平衡。03d302FlkFykyFly则：轴力方程为：330d)(lFyyfyFyN求地桩的缩短量δ：EAFlyyEAlFyEAyFlllN4dd)(033023333ylFflFk即：yFN(y)2-7简单托架及其受力如图所示，水平杆BC的长度l保持不变，斜杆AB的长度可随夹角θ的变化而改变。两等直杆由同一材料制造，且材料的许用拉应力与许用压应力相等。要求两杆内的应力同时达到许用应力，且结构的总重量为最小时，试求：（1）两杆的夹角θ值；（2）两杆横截面面积的比值解：求各杆内力及应力sincoscossin1][sin][coscossin][FllFlFlAlAVBCBCABAB由题义，各杆应力达到许用应力，则：sin][cossin][FAFABCAB要求结构的总重量为最小即结构总体积最小，其体积为：(拉)sinFFNABsinABABNABABAFAFsincosFFNBC(压)sincosBCBCNBCBCAFAFFFNABFNBCB0ddV令：得：445474.542tan3cos1BCABAA则：即：两杆的夹角θ值为两杆横截面面积的比值为445432-9图示桁架结构，各杆都由两个相同的等边角钢组成。已知材料的许用应力[σ]=170MPa，...