材料力学第9章 梁的挠度和刚度计算VIP免费

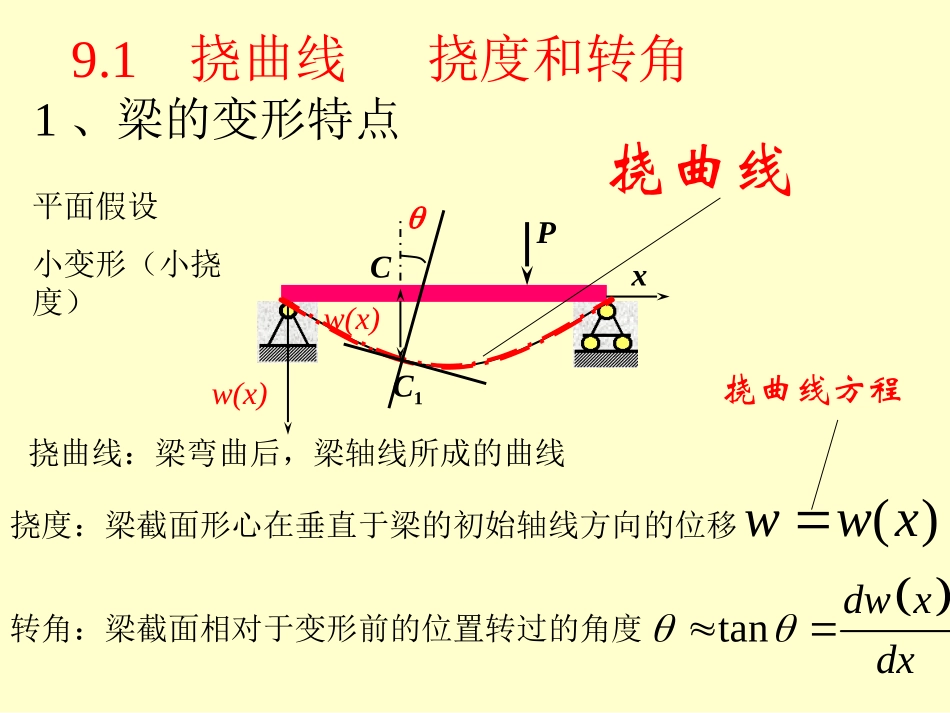
第9章平面弯杆弯曲变形与刚度计算9.1挠曲线挠度和转角9.2挠曲线近似微分方程9.3积分法求梁的变形9.4叠加法求梁的变形9.5梁的刚度条件与合理刚度设计9.6用变形比较法解简单超静定梁1、梁的变形特点PxCC1w(x)w(x)挠度：梁截面形心在垂直于梁的初始轴线方向的位移转角：梁截面相对于变形前的位置转过的角度挠曲线()wwxtandwxdx9.1挠曲线挠度和转角平面假设小变形（小挠度）挠曲线：梁弯曲后，梁轴线所成的曲线挠曲线方程2，意义工业厂房钢筋混凝土吊梁600~500][LLf普通机车主轴3.00][符号给定：正值的挠度向下，负值的向上；正值的转角为顺时针转相，负值的位逆时针转向3，影响变形的因素不计由小变形条件，x%3,10的的影响只有时MQhL4，计算变形的方法积分法、叠加法、能量法、………1、挠曲线近似微分方程zzEIxM)(1xo()()zzMxwxEI挠曲线近似微分方程小变形3221()()(1)wxwxw2()1()zzMxwwxEIM>022()0dwxdxM<022()0dwxdx9.2挠曲线近似微分方程()wx()()EIwxMxzzEIxM)(1*思考：）（若、xMM2常量若、M11、挠曲线方程（弹性曲线）()()EIwxMx1()()dEIwxMxxC12()(()d)dEIwxMxxxCxC9.3积分法求梁的变形2、边界条件、连续条件PDwxLPABCwxLa0,0xw,0xLw1212,xawwww0,0xw0,0xw*注意问题()()EIwxMx什么时候需要分段积分？如何确定极值？PL1L2ABC例9.1求等截面直梁的弹性曲线、最大挠度及最大转角。弯矩方程()()MxPLx微分方程的积分边界条件、连续条件PLxw()()()EIwxMxPLx211()2EIwPLxC3121()6EIwPLxCxC321(0)06EIwPLC211(0)02EIwPLC2112CPL3216CPL弹性曲线方程最大挠度及最大转角2()(3)6PxwxLxEI2max()2PLLEI3max()3PLwwLEIxPLwLq0BA例9.2均布荷载下的简支梁，EI已知，求挠度及两端截面的转角。maxw解：1确定反力2求出弯矩方程2AqlF2BqlF2122qlMxxqxxw3微分方程的积分4边界条件、连续条件21()22qlEIwxMxqxx14311(0)00()0102412EIwDEIwlqlqllClD2124qlC321431116412412qlEIwqxxCqlEIwqxxCxD5梁的转角方程和挠曲线方程332343164241241224qlqlEIqxxqlqlEIwqxxx6梁的最大挠度：根据对称性4332max215|242122242384llqllqllqlEIwEIwqEI7梁两端的转角303332|241|642424AxBxlqlEIEIqlqlqlEIEIqll例9.3集中力下的简支梁，EI已知，求挠曲线方程和转角方程，最大挠度及最大转角。FalAB解：1确定反力2求出弯矩方程120,,AyFbMxFxxxalFbMxxFxalxalD3微分方程的积分1122()()FbEIwxMxxlFbEIwxMxxFxalBFaFlAFbFl21122222122FbEIwxClFbEIwxFxaCl积分一次：3111332226166FbEIwxCxDlFbEIwxFxalCxD再积分一次：4边界条件、连续条件12121212()()()()EIwaEIwaCCEIwaEIwaDD1133222(0)001()0660EIwDFbEIwllFlalClD边界条件连续条件积分成数为12221206DDFbCClbl222122222261226FbFbEIwxlbllFbEIwxFxalFblbl322133222661666FbFbEIwxlbxllFbEIwxFxalFblbxl5梁的转角方程和挠曲线方程6最大转角0max2max|6|6616AxBxlBFabEIEIlblFabEIEIlalifabthenFablalEIifabthenFlEI6最大挠度222122222max13max00262333()9348FbFbwhenwxlbllalbaablbxifabthenxaFbwwxlbEIlifabthenxaFlwEIACEI例、试用积分法求图示梁的转角方程和挠曲线方程，并求截面的转角和截面的挠度。设常量。xCDAB/2l/2l/2lw解：1确定反力2求出弯矩...