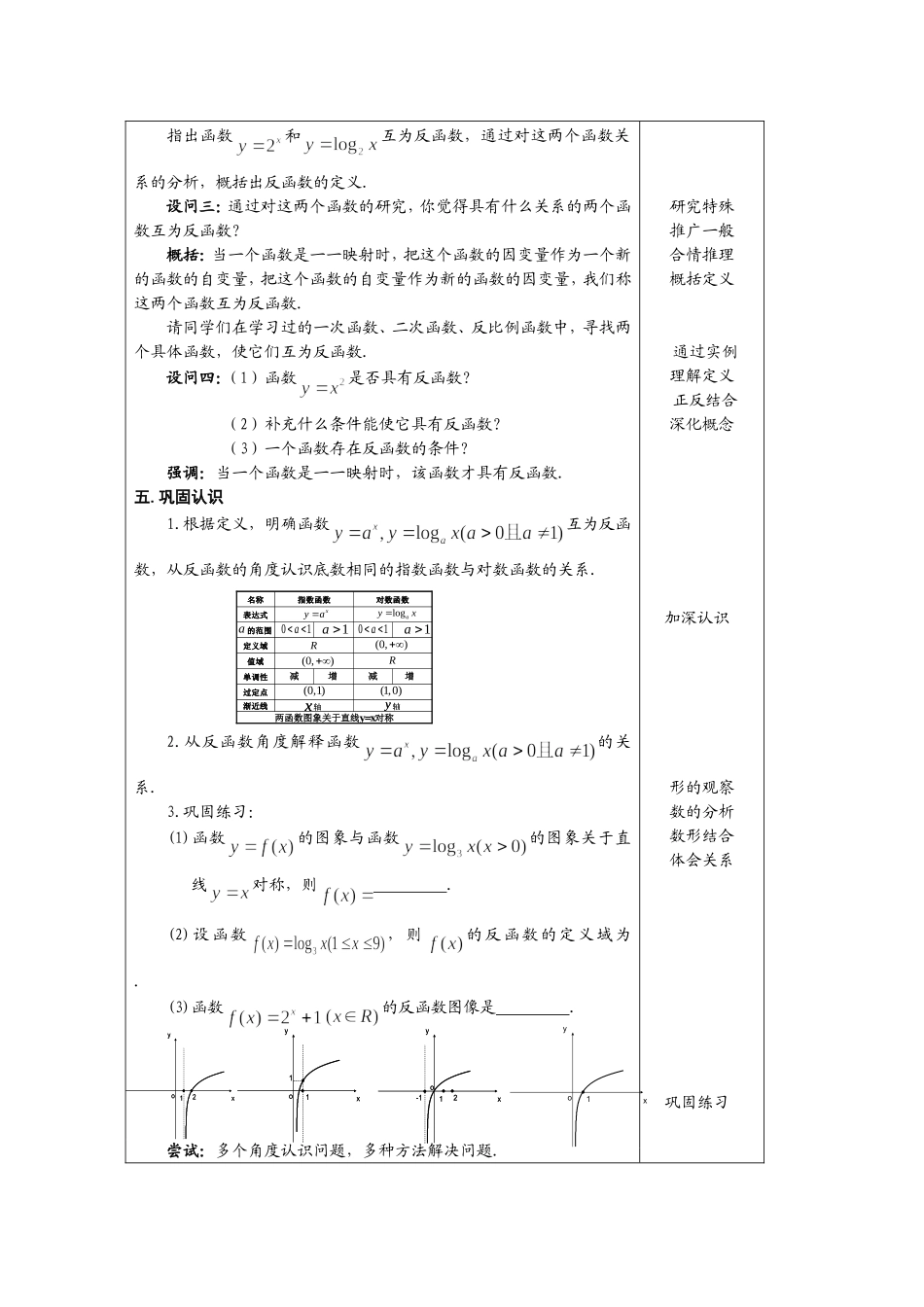
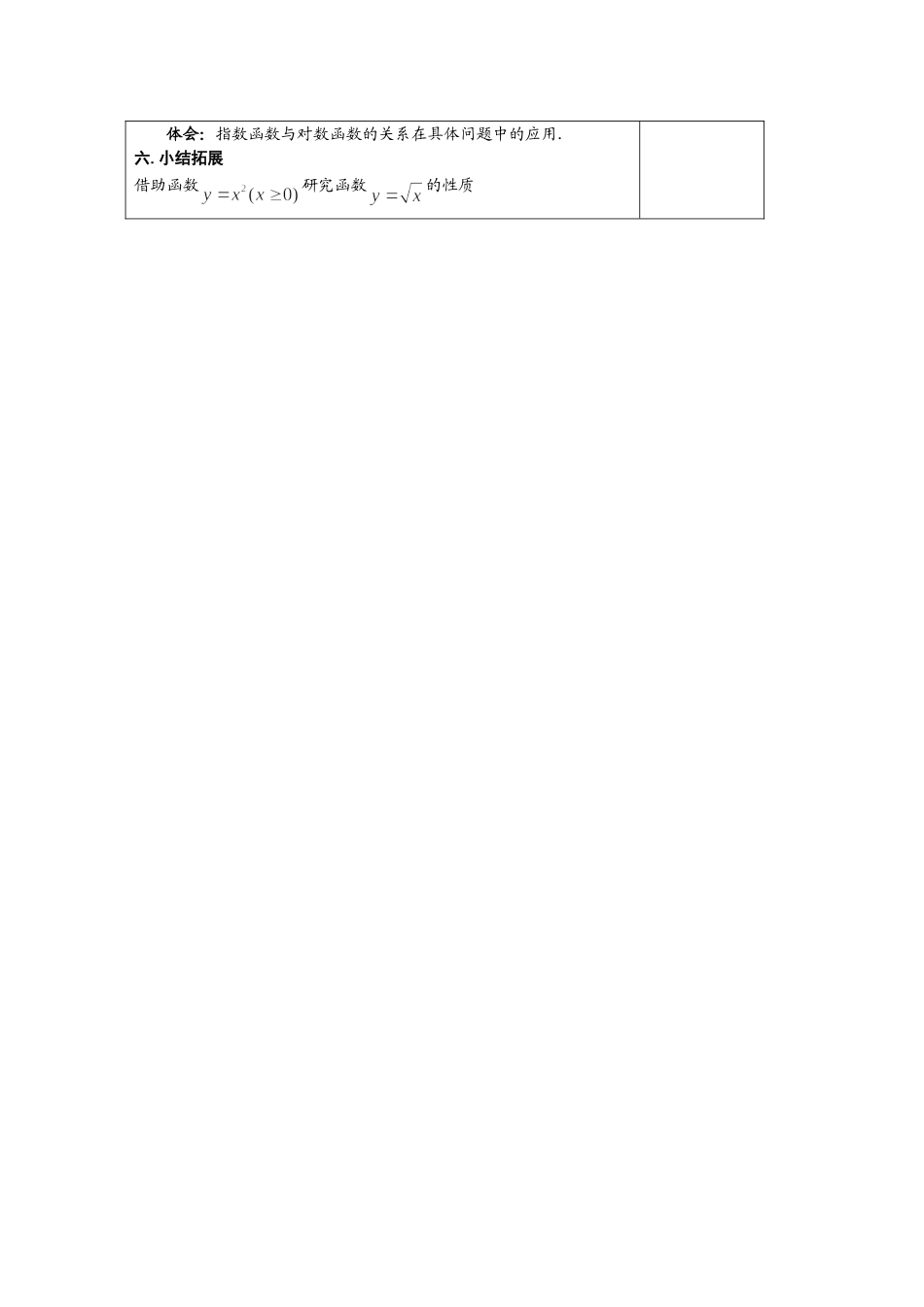
学校哈师大附中教师周妍时间2008年10月课题指数函数与对数函数关系(人教B版)教龄4年教学目标学生在对比函数的过程中,知道同底的指数函数和对数函数互为反函数,并从反函数角度认识指数函数与对数函数的关系,从而培养学生观察、分析、探究、概括的能力,渗透数形结合的思想,并使学生掌握从特殊到一般的研究问题的方法.教学重点指数函数与对数函数关系教学难点反函数概念教学基本流程创设情境发现关系探究原因概括定义巩固认识小结拓展教学过程设计意图一.问题引入1.利用“鱼化石”实例提出问题,引出指数函数和对数函数的关系在实际中的应用.2.复习指数函数、对数函数有关内容(1)以函数为例,在同一坐标系中用描点法画出两函数图象;…8421…y…3210-1-2-3…x181412…8421…y…3210-1-2-3…x1814122xy…3210-1-2-3…y…8421…x181412…3210-1-2-3…y…8421…x1814122logyxxyoxyoxyo2xy2logyx1234567812345678-3-2-1-3-2-1(2)结合图象,回顾这两个函数的性质.二.发现关系设问一:通过对比发现这两个函数有很多联系,具体在哪些方面有怎样的关系?归纳:定义域值域互换;单调性一致;增长速度存在差异;图象关于直线对称…三.探究原因设问二:为什么会有如此多的联系?得出:两函数自变量和因变量发生了互换.四.概括定义创设情境激发兴趣解决问题发现关系复习提问作以铺垫引导学生对比观察发现关系启发学生深入探究指出函数和互为反函数,通过对这两个函数关系的分析,概括出反函数的定义.设问三:通过对这两个函数的研究,你觉得具有什么关系的两个函数互为反函数?概括:当一个函数是一一映射时,把这个函数的因变量作为一个新的函数的自变量,把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数.请同学们在学习过的一次函数、二次函数、反比例函数中,寻找两个具体函数,使它们互为反函数.设问四:(1)函数是否具有反函数?(2)补充什么条件能使它具有反函数?(3)一个函数存在反函数的条件?强调:当一个函数是一一映射时,该函数才具有反函数.五.巩固认识1.根据定义,明确函数互为反函数,从反函数的角度认识底数相同的指数函数与对数函数的关系.2.从反函数角度解释函数的关系.3.巩固练习:(1)函数的图象与函数的图象关于直线对称,则.(2)设函数,则的反函数的定义域为.(3)函数的反函数图像是.尝试:多个角度认识问题,多种方法解决问题.研究特殊推广一般合情推理概括定义通过实例理解定义正反结合深化概念加深认识形的观察数的分析数形结合体会关系巩固练习21xyo21xyo1xyo11xyo11xyo21xyo-121xyo-1渐近线过定点单调性值域定义域的范围表达式名称对数函数指数函数渐近线过定点单调性值域定义域的范围表达式名称对数函数指数函数alogayxxya01a01a1a1a(0,)(0,)RR增增减减y轴y轴x轴x轴(1,0)(0,1)两函数图象关于直线y=x对称体会:指数函数与对数函数的关系在具体问题中的应用.六.小结拓展借助函数研究函数的性质