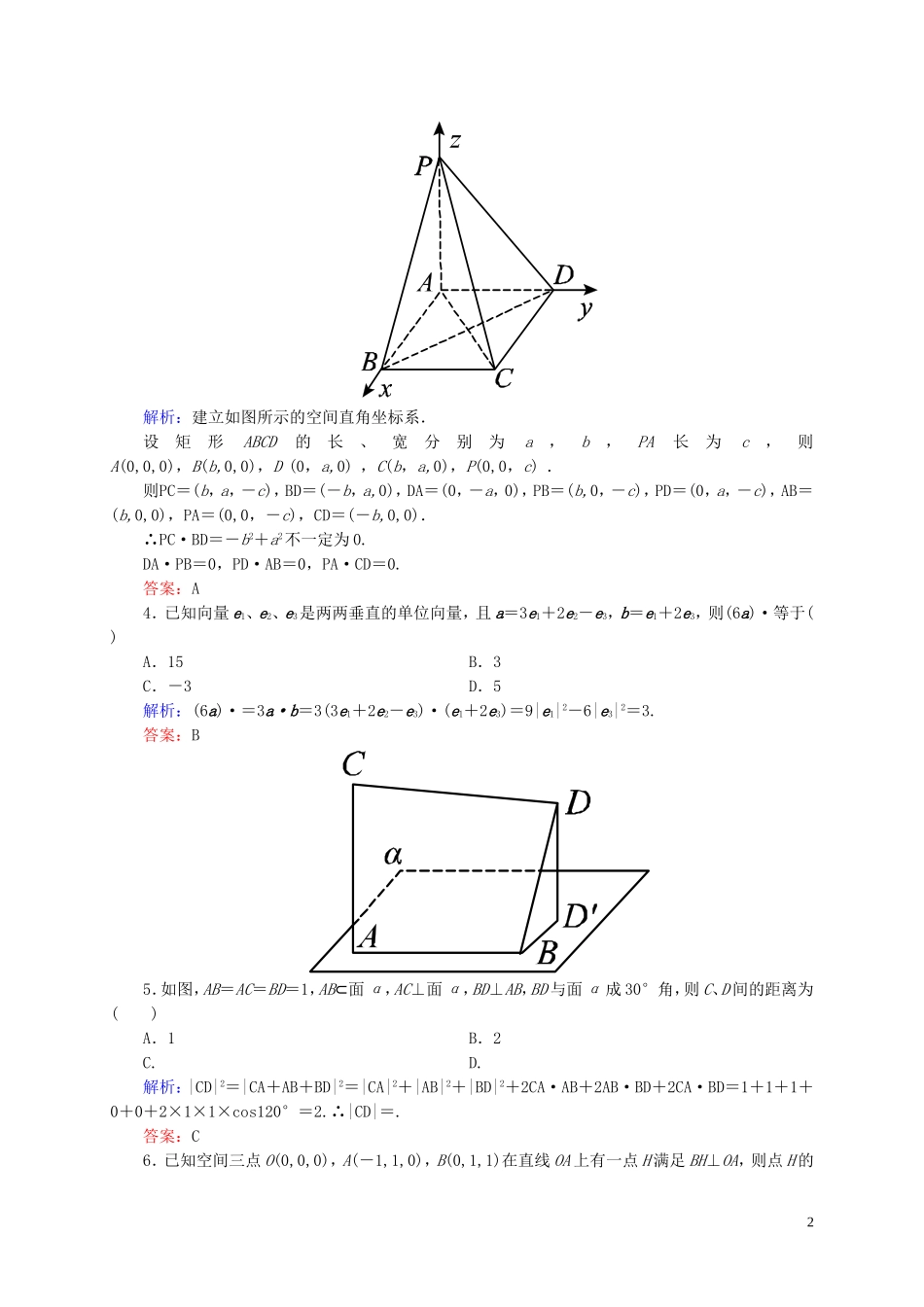
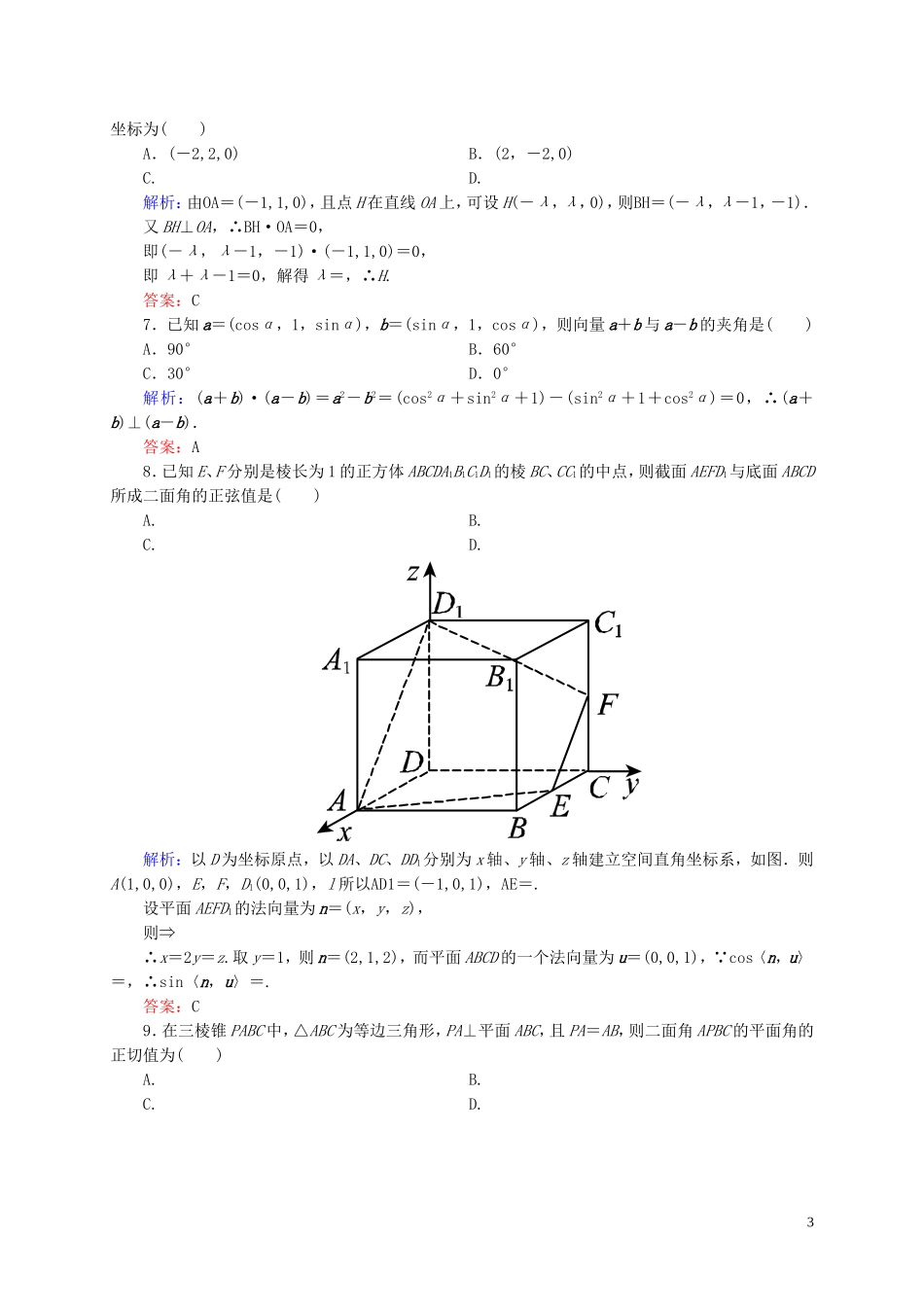
单元测评(三)空间向量与立体几何(时间:90分钟满分:120分2014.4)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.1.以下四组向量中,互相平行的组数为()①a=(2,2,1),b=(3,-2,-2);②a=(8,4,-6),b=(4,2,-3);③a=(0,-1,1),b=(0,3,-3);④a=(-3,2,0),b=(4,-3,3)A.1组B.2组C.3组D.4组解析: ②中a=2b,∴a∥b;③中a=-b,∴a∥b;而①④中的向量不平行.答案:B2.在以下命题中,不正确的个数为()①|a|-|b|=|a+b|是a,b共线的充要条件;②若a∥b,则存在唯一的实数λ,使a=λb;③对空间任意一点O和不共线的三点A,B,C,若OP=2OA-2OB-OC,则P,A,B,C四点共面;④若{a,b,c}为空间的一组基底,则{a+b,b+c,c+a}构成空间的另一组基底;⑤|(a·b)·c|=|a|·|b|·|c|.A.2个B.3个C.4个D.5个解析:①|a|-|b|=|a+b|⇒a与b共线,但a与b共线时|a|-|b|=|a+b|不一定成立,故不正确;②b需为非零向量,故不正确;③因为2-2-1≠1,由共面向量定理知,不正确;④由基底的定义知正确;⑤由向量的数量积的性质知,不正确.答案:C3.如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是()A.PC与BDB.DA与PBC.PD与ABD.PA与CD1解析:建立如图所示的空间直角坐标系.设矩形ABCD的长、宽分别为a,b,PA长为c,则A(0,0,0),B(b,0,0),D(0,a,0),C(b,a,0),P(0,0,c).则PC=(b,a,-c),BD=(-b,a,0),DA=(0,-a,0),PB=(b,0,-c),PD=(0,a,-c),AB=(b,0,0),PA=(0,0,-c),CD=(-b,0,0).∴PC·BD=-b2+a2不一定为0.DA·PB=0,PD·AB=0,PA·CD=0.答案:A4.已知向量e1、e2、e3是两两垂直的单位向量,且a=3e1+2e2-e3,b=e1+2e3,则(6a)·等于()A.15B.3C.-3D.5解析:(6a)·=3a·b=3(3e1+2e2-e3)·(e1+2e3)=9|e1|2-6|e3|2=3.答案:B5.如图,AB=AC=BD=1,AB⊂面α,AC⊥面α,BD⊥AB,BD与面α成30°角,则C、D间的距离为()A.1B.2C.D.解析:|CD|2=|CA+AB+BD|2=|CA|2+|AB|2+|BD|2+2CA·AB+2AB·BD+2CA·BD=1+1+1+0+0+2×1×1×cos120°=2.∴|CD|=.答案:C6.已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1)在直线OA上有一点H满足BH⊥OA,则点H的2坐标为()A.(-2,2,0)B.(2,-2,0)C.D.解析:由OA=(-1,1,0),且点H在直线OA上,可设H(-λ,λ,0),则BH=(-λ,λ-1,-1).又BH⊥OA,∴BH·OA=0,即(-λ,λ-1,-1)·(-1,1,0)=0,即λ+λ-1=0,解得λ=,∴H.答案:C7.已知a=(cosα,1,sinα),b=(sinα,1,cosα),则向量a+b与a-b的夹角是()A.90°B.60°C.30°D.0°解析:(a+b)·(a-b)=a2-b2=(cos2α+sin2α+1)-(sin2α+1+cos2α)=0,∴(a+b)⊥(a-b).答案:A8.已知E、F分别是棱长为1的正方体ABCDA1B1C1D1的棱BC、CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是()A.B.C.D.解析:以D为坐标原点,以DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,如图.则A(1,0,0),E,F,D1(0,0,1),l所以AD1=(-1,0,1),AE=.设平面AEFD1的法向量为n=(x,y,z),则⇒∴x=2y=z.取y=1,则n=(2,1,2),而平面ABCD的一个法向量为u=(0,0,1), cos〈n,u〉=,∴sin〈n,u〉=.答案:C9.在三棱锥PABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则二面角APBC的平面角的正切值为()A.B.C.D.3解析:设PA=AB=2,建立如图所示的空间直角坐标系.则B(0,2,0),C(,1,0),P(0,0,2),∴BP=(0,-2,2),BC=(,-1,0).设n=(x,y,z)是平面PBC的一个法向量.则即令y=1,则x=,z=1.即n=.易知m=(1,0,0)是平面PAB的一个法向量.则cos〈m,n〉===.∴正切值tan〈m,n〉=.答案:A10.已知OA=(1,2,3),OB=(2,1,2),OP=(1,1,2),点Q在直线OP上运动,则当QA·QB取得最小值时,点Q的坐标为()A.B.C.D.解析: Q在OP上,∴可设Q(x,x,2x),则QA=(1-x,2-x,3-2x),QB=(2-x,1-x,2-2x).∴QA·QB=6x2-16x+10,∴x=时,QA·QB最小,这时Q.答案...