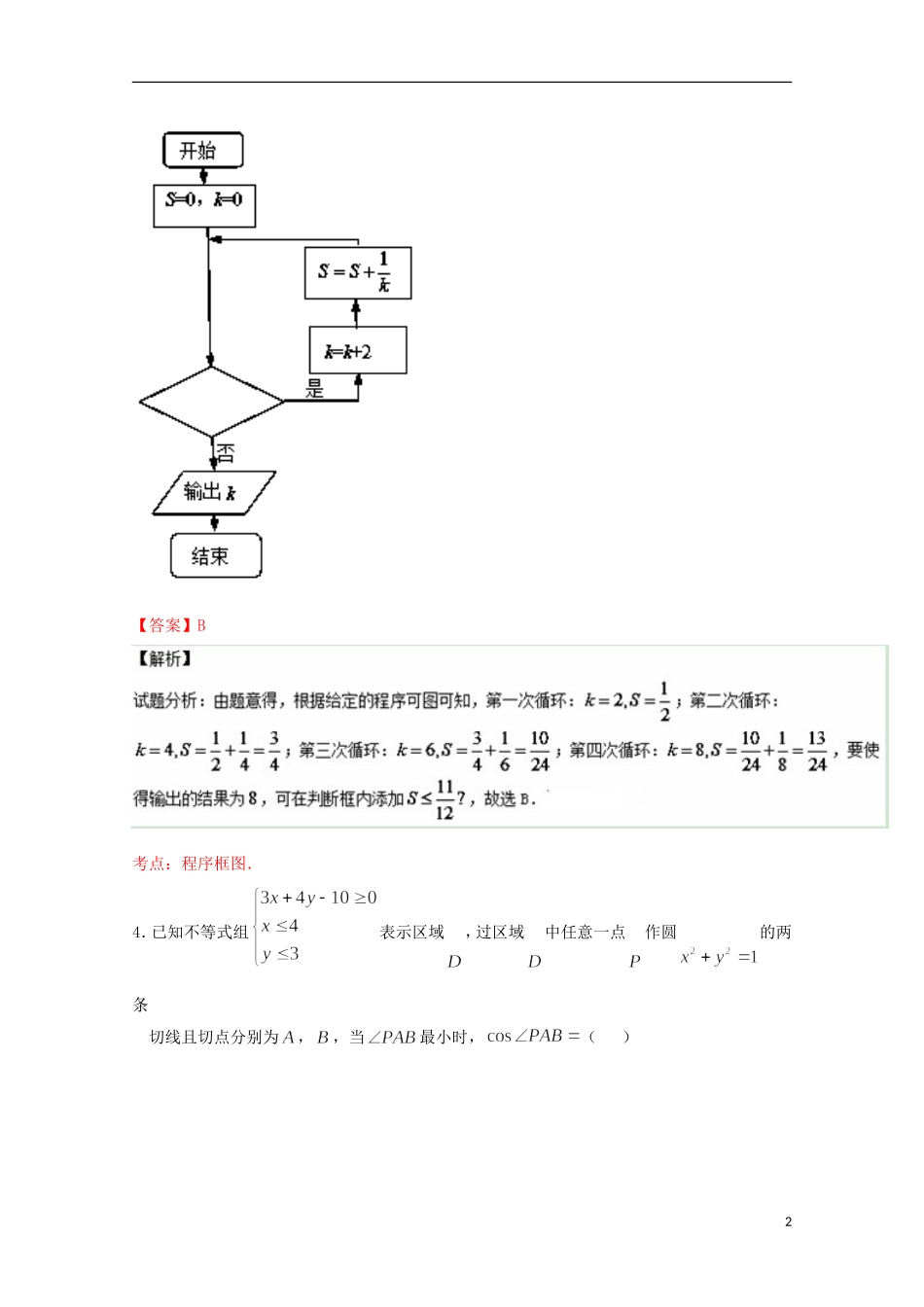
湖北省沙市中学2015-2016学年高二数学下学期第六次半月考试题文(含解析)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若复数是实数,则实数()A.1B.C.D.【答案】B【解析】试题分析:由题意得,,令,故选B.考点:复数的运算及复数的概念.2.集合,,从,中各任意取一个数,则这两数之和等于4的概率是()A.B.C.D.【答案】C考点:古典概型及其概率的计算.3.执行如图所示的程序框图,若输出的值为8,则判断框内可填入的条件是()A.B.C.D.1【答案】B考点:程序框图.4.已知不等式组表示区域,过区域中任意一点作圆的两条切线且切点分别为,,当最小时,()2A.B.C.D.【答案】B【解析】试题分析:作出不等式组表示的平面区域,如图所示,要使的最小时,则使得最大,因为,所以只要最小即可,在到圆心的距离最小即可,由图象可知,当垂直直线,此时,设,则,即,此时,即,故选B.考点:简单的线性规划的应用.5.已知直线()与圆交于不同的两点、,是坐标原点,且有,那么的取值范围是()3A.B.C.D.【答案】C考点:直线与圆的位置关系;向量的应用.6.在ABC中,060,2,6ABCABBC,在BC上任取一点D,则使ABD是以BAD为钝角的三角形的概率为()A.16B.13C.12D.23【答案】B【解析】试题分析:由题意得,试验发生包含的时间对应的长度为一条线段,要使得ABD是以BAD为钝角的三角形,此时情况的边界为,此时,所以要是的,必有,所以概率为,故选B.考点:几何概型及其概率的求解.【方法点晴】本题主要考查了几何概型及其概率的求解,对应几何概型的求解中,要根据题意判4断出几何概型的度量关系——常见的几何概型的度量有长度度量、面积度量、体积度量和角度度量等,本题的解答中要使得ABD是以BAD为钝角的三角形,此时情况的边界为,得出是解答问题的关键,着重考查了分析问题和解答问题的能力,属于基础题.7.圆与圆的公共弦长为()A.5B.6C.25D.26【答案】C考点:圆的弦长公式.8.直线yxb与曲线21xy有且只有一个公共点,则b的取值范围是()A.||2bB.112bb或C.11bD.112bb或【答案】D【解析】试题分析:由21xy,可化简为,所以表示的图形是以原点为圆心,半径为的一个半圆,如图所示,要使得与直线yxb只有一个公共点,则当yxb过点和时,此时,当直线在第四象限与圆相切时,此时,5所以实数的取值范围是112bb或,故选D.考点:直线与圆位置关系的应用.9.已知函数的图象如图所示,则不等式的解集为()A.(-∞,12)∪(12,2)B.(-∞,0)∪(12,2)C.(-∞,12)∪(12,+∞)D.(-∞,12)∪(2,+∞)【答案】B考点:导数与函数单调性的关系.10.已知、为双曲线的左、右焦点,点P在C上,,则点P到x轴的距离为()A.B.C.6D.【答案】B【解析】试题分析:设,不妨设,由双曲线的方程可知,根据双曲线的定义可知,即,在中,根据余弦定理,得,即,解得,设点的距离为,则,解得,故选B.考点:双曲线的定义;余弦定理;三角形的面积公式.11.已知函数cossin4fxfxx,则4f()A.2B.21C.1D.0【答案】C考点:导数的运算;函数求值.【方法点晴】本题主要考查了导数的运算及函数的求值问题,其中熟记导数的运算公式及导数的四则运算公式和函数在某点处的导数的意义是解答此类问题的关键,本题的解答中,利用导7数的运算公式得,令,求出是解答本题的关键,着重考查学生的推理与运算能力,属于基础题.12.若曲线xmfxex在(,0)上存在垂直y轴的切线,则实数m取值范围为()A.24(,]eB.24(0,]eC.(,4]D.(0,4]【答案】B【解析】试题分析:由曲线xmfxex在(,0)上存在垂直y轴的切线,可得在上有解,得在上有解,设,由,可得当时,,则单调递减;当时,,则单调递增,可知在处取得极大值,且为最大值,且当时,,所以实数,故选B.考点:利用导数研究曲线在某点处的切线方程;利用导数求解函数在区间上的最值.【方法点晴】本...