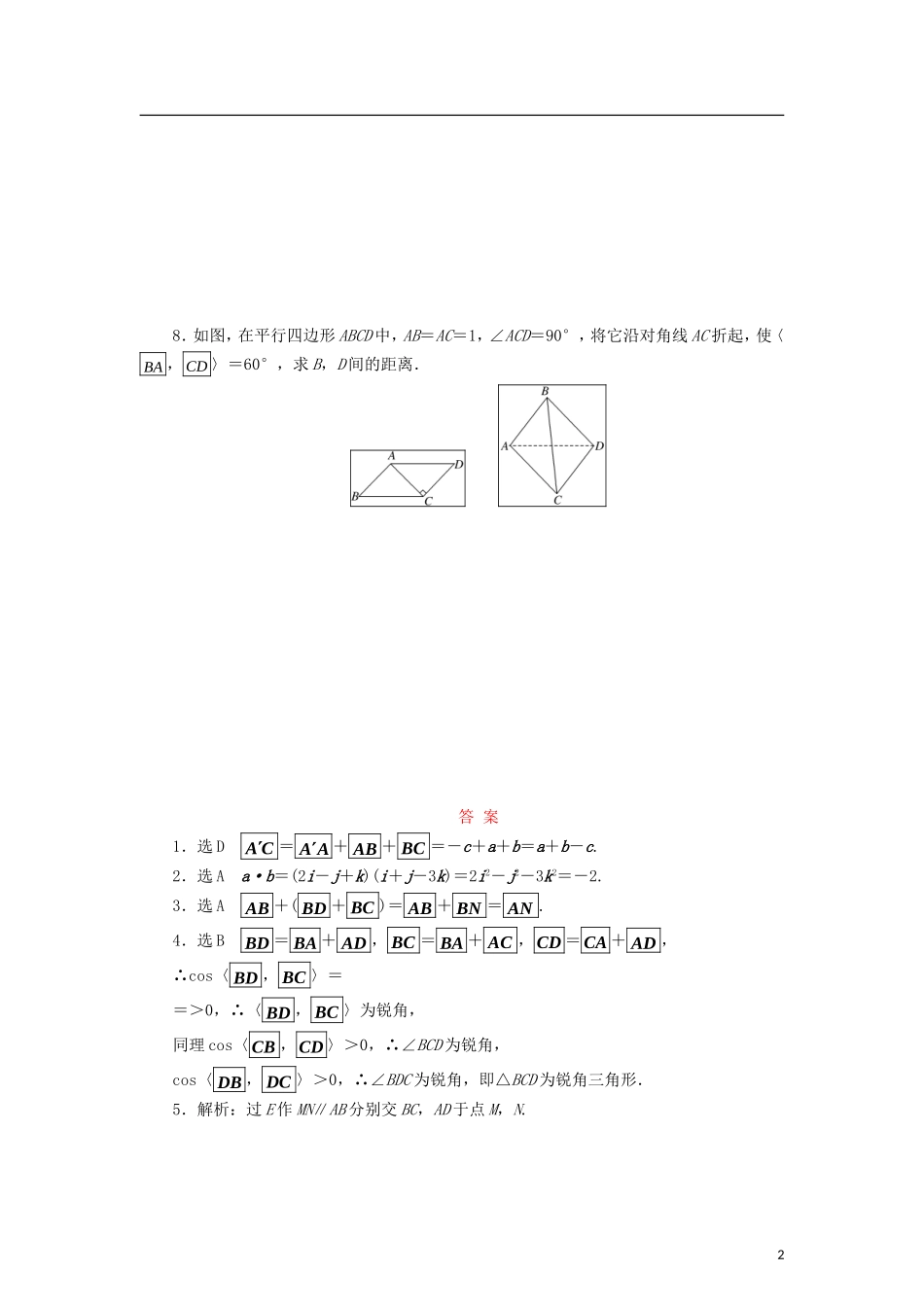
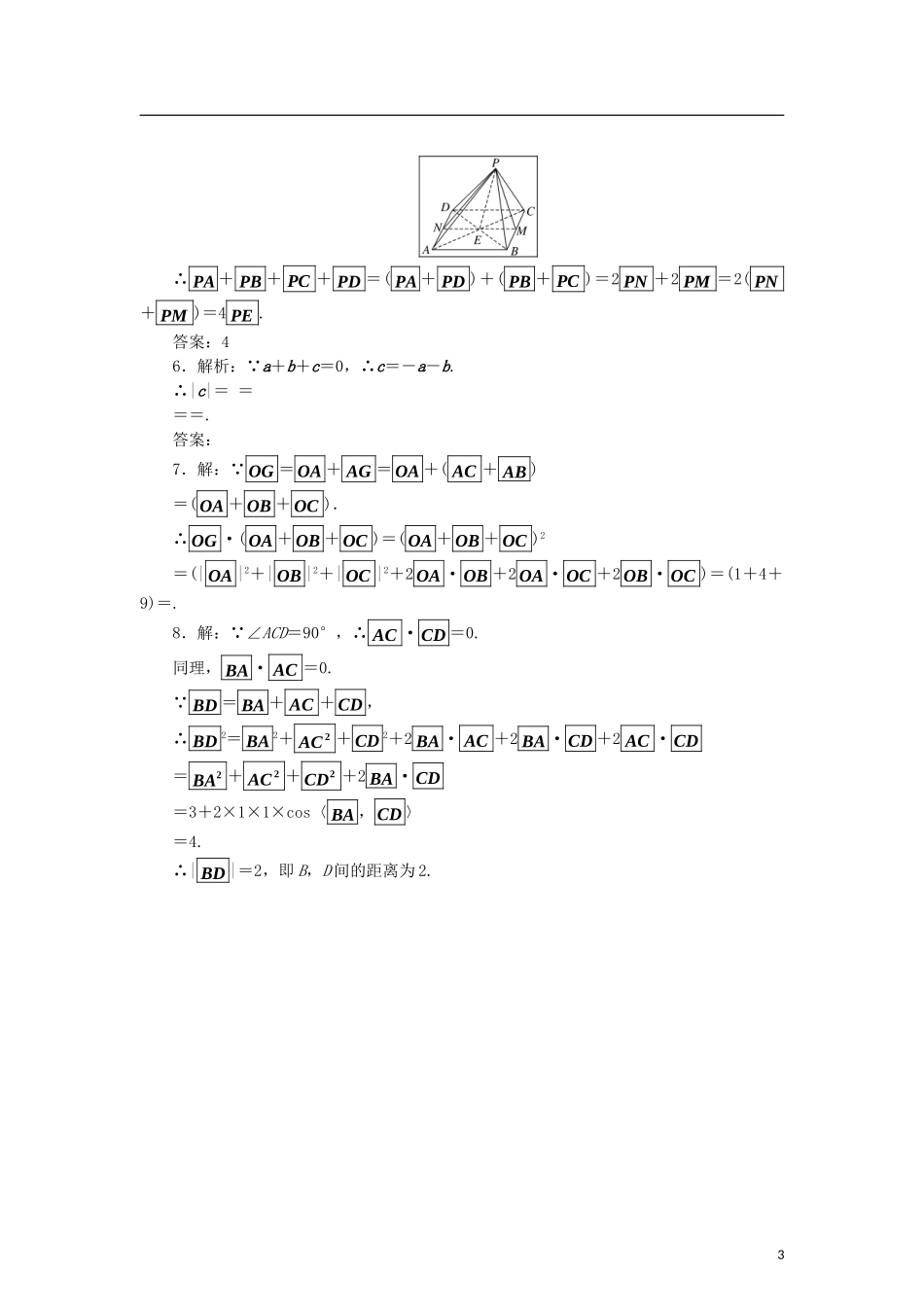
课时跟踪训练(六)空间向量的运算1.如图,在平行六面体ABCD-A′B′C′D′中,设AB�=a,AD�=b,1AA�=c,则下列与向量AC�相等的表达式是()A.-a+b+cB.-a-b+cC.a-b-cD.a+b-c2.已知i,j,k是两两垂直的单位向量,a=2i-j+k,b=i+j-3k,则a·b=()A.-2B.-1C.±1D.23.如图,已知空间四边形ABCD,连接AC,BD.设M,N分别是BC,CD的中点,则AB�+(BD�+BC�)=()A.AN�B.CN�C.BC�D.BC�4.设A,B,C,D是空间不共面的四点,且满足AB�·AC�=AC�·AD�=AB�·AD�=0,则△BCD为()A.钝角三角形B.锐角三角形C.直角三角形D.不确定5.如图,▱ABCD的对角线AC和BD交于点E,P为空间任意一点,若PA�+PB�+PC�+PD�=xPE�,则x=________.6.设a,b,c满足a+b+c=0,且a⊥b,|a|=1,|b|=2,则|c|=________.7.在四面体O-ABC中,棱OA,OB,OC两两互相垂直,且|OA�|=1,|OB�|=2,|OC�|=3,G为△ABC的重心,求OG�·(OA�+OB�+OC�)的值.18.如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使〈BA�,CD�〉=60°,求B,D间的距离.答案1.选DAC�=AA�+AB�+BC�=-c+a+b=a+b-c.2.选Aa·b=(2i-j+k)(i+j-3k)=2i2-j2-3k2=-2.3.选AAB�+(BD�+BC�)=AB�+BN�=AN�.4.选BBD�=BA�+AD�,BC�=BA�+AC�,CD�=CA�+AD�,∴cos〈BD�,BC�〉==>0,∴〈BD�,BC�〉为锐角,同理cos〈CB�,CD�〉>0,∴∠BCD为锐角,cos〈DB�,DC�〉>0,∴∠BDC为锐角,即△BCD为锐角三角形.5.解析:过E作MN∥AB分别交BC,AD于点M,N.2∴PA�+PB�+PC�+PD�=(PA�+PD�)+(PB�+PC�)=2PN�+2PM�=2(PN�+PM�)=4PE�.答案:46.解析:∵a+b+c=0,∴c=-a-b.∴|c|====.答案:7.解:∵OG�=OA�+AG�=OA�+(AC�+AB�)=(OA�+OB�+OC�).∴OG�·(OA�+OB�+OC�)=(OA�+OB�+OC�)2=(|OA�|2+|OB�|2+|OC�|2+2OA�·OB�+2OA�·OC�+2OB�·OC�)=(1+4+9)=.8.解:∵∠ACD=90°,∴AC�·CD�=0.同理,BA�·AC�=0.∵BD�=BA�+AC�+CD�,∴BD�2=BA�2+2AC�+CD�2+2BA�·AC�+2BA�·CD�+2AC�·CD�=2BA�+2AC�+2CD�+2BA�·CD�=3+2×1×1×cos〈BA�,CD�〉=4.∴|BD�|=2,即B,D间的距离为2.3