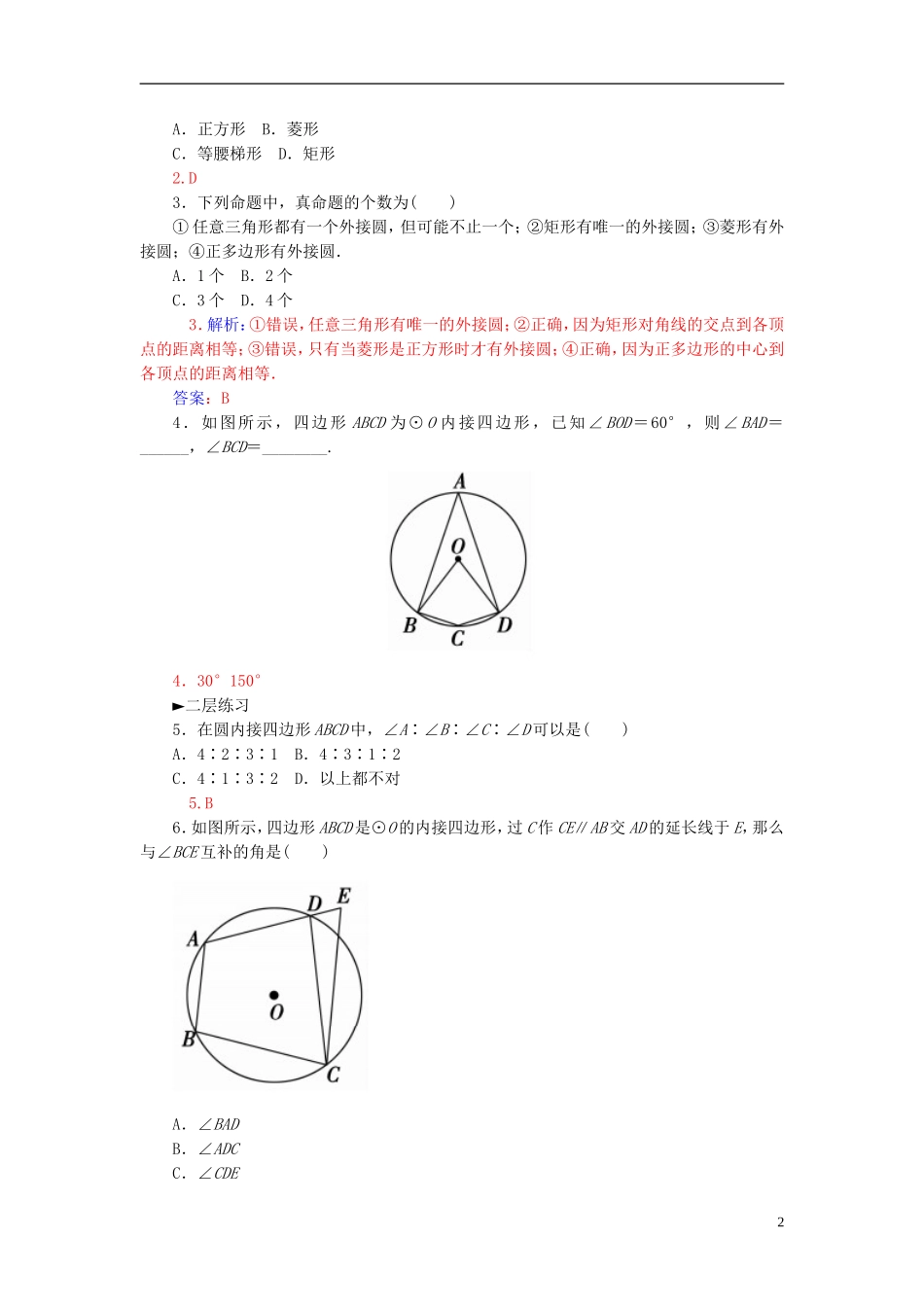
2.2圆内接四边形的性质与判定定理1.圆内接多边形的定义.如果多边形的所有顶点都在一个圆上,那么这个多边形叫做____________,这个圆叫做多边形的________.2.圆内接四边形的性质定理1:圆内接四边形的对角________.圆内接四边形的性质定理2:圆内接四边形的外角等于它的内角的________.3.圆内接四边形的判定定理.如果一个四边形的对角________,那么这个四边形的四个顶点共圆.4.判定定理的推论:如果四边形的一个外角等于它的内角的________,那么这个四边形四个顶点共圆.5.如图,矩形ABCD的对角线AC和BD相交于点O,求证:A、B、C、D四点共圆.预习导学1.圆内接多边形外接圆2.互补对角3.互补4.对角5.证明:四边形ABCD为矩形,∴OA=OC,OB=OD,AC=DB,∴OA=OB=OC=OD. 点A、B、C、D到O点的距离相等,∴A、B、C、D这四个点在以点O为圆心,OA为半径的同一个圆上.►一层练习1.已知四边形ABCD是圆内接四边形,下列结论中正确的个数有()①如果∠A=∠C,则∠A=90°;②如果∠A=∠B,则四边形ABCD是等腰梯形;③∠A的外角与∠C的外角互补;④∠A∶∠B∶∠C∶∠D可以是1∶2∶3∶4.A.1个B.2个C.3个D.4个1.B2.圆内接平行四边形一定是()1A.正方形B.菱形C.等腰梯形D.矩形2.D3.下列命题中,真命题的个数为()①任意三角形都有一个外接圆,但可能不止一个;②矩形有唯一的外接圆;③菱形有外接圆;④正多边形有外接圆.A.1个B.2个C.3个D.4个3.解析:①错误,任意三角形有唯一的外接圆;②正确,因为矩形对角线的交点到各顶点的距离相等;③错误,只有当菱形是正方形时才有外接圆;④正确,因为正多边形的中心到各顶点的距离相等.答案:B4.如图所示,四边形ABCD为⊙O内接四边形,已知∠BOD=60°,则∠BAD=______,∠BCD=________.4.30°150°►二层练习5.在圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是()A.4∶2∶3∶1B.4∶3∶1∶2C.4∶1∶3∶2D.以上都不对5.B6.如图所示,四边形ABCD是⊙O的内接四边形,过C作CE∥AB交AD的延长线于E,那么与∠BCE互补的角是()A.∠BADB.∠ADCC.∠CDE2D.∠DEC6.C7.如图所示,四边形ABCD为⊙O的内接四边形,点E为AB延长线上一点,∠CBE=40°,则∠AOC等于()A.20°B.40°C.80°D.100°7.C8.如图所示,PA为⊙O直径,PC为⊙O的弦,过AC的中点H作PC的垂线交PC的延长线于点B.若HB=6,BC=4,则⊙O的直径为()A.10B.13C.15D.208.解析:连PH及CH,由圆内接四边形的性质定理有∠BCH=∠A,则△PAH∽△HCB,=,又CH=HA,则PA=13.答案:B9.若圆内接四边形中3个相邻的内角比为5∶6∶4,则这个四边形中最大的内角为________,最小的内角为________.9.120°60°10.如图,⊙O的内接四边形BCED,延长ED、CB交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=________,CE=________.310.解析:由圆内接四边形的性质定理有∠ADB=∠C,∠ABD=∠E.则△ABD∽△AEC,则==代入数据即得DE=5,CE=2.答案:52►三层练习11.如下图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则的值为________.11.12.如图所示,在△ABC中,AD=DB,DF⊥AB交AC于点F,AE=EC,EG⊥AC交AB于点G.(1)求证:点D、E、F、G四点共圆;(2)求证:点G、B、C、F四点共圆.12.证明:(1)连接GF,由DF⊥AB,EG⊥AC,知∠GDF=∠GEF=90°,4∴GF中点到点D、E、F、G四点距离相等.∴点D、E、F、G四点共圆.(2)连接DE.由AD=DB,AE=EC,知DE∥BC,∴∠ADE=∠B.又由(1)中点D、E、F、G四点共圆,∴∠ADE=∠GFE.∴∠GFE=∠B.∴∠B+∠GFC=180°.∴点G、B、C、F四点共圆.13.如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.(1)证明:∠D=∠E;(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.13.证明:(1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE.由已知得∠CBE=∠E,故∠D=∠E.(2)如图设BC的中点为N,连接MN,则由MB=MC知MN⊥BC,故O在直线MN上.5又AD不是⊙O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD.所以AD∥BC,故∠A=∠CBE.又∠CBE...