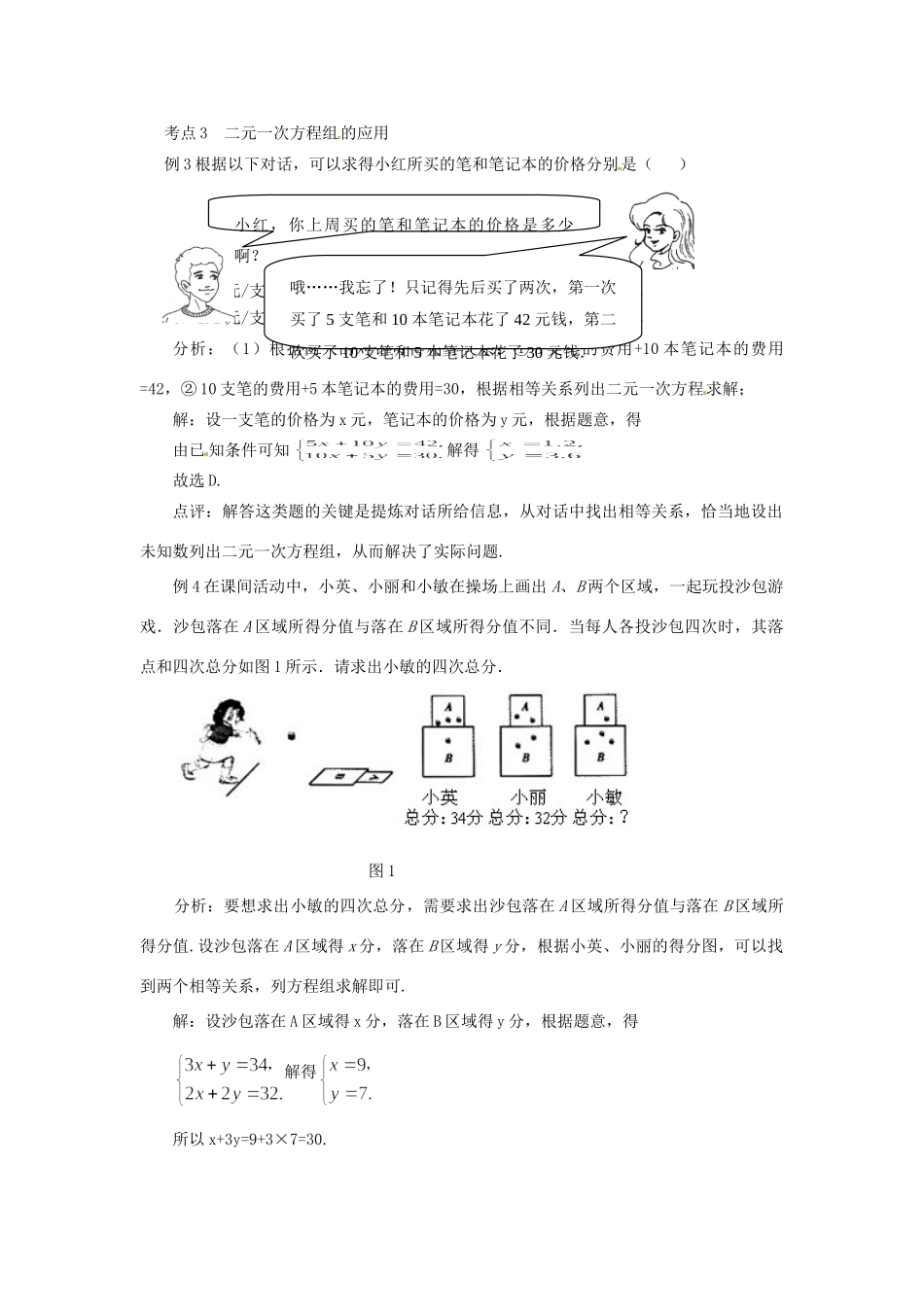
山东省滨州市无棣县埕口中学九年级数学二元一次方程组考点面对面二元一次方程组是初中数学的基础知识,也是考试必考的内容之一,现归纳常见考点,以帮助大家熟悉考点,更好地掌握这章内容.考点1二元一次方程组的解例1已知是二元一次方程组的解,则2m-n的为()A.4B.2C.-4D.6分析:已知二元一次方程组的解,求字母系数有关的代数式的值,可将方程组的解代入原方程组,求得m,n的值,再计算代数式的值.解:把代入原方程组,得,解得,所以2m-n=4.故选A.点评:本题主要考查方程组的解的意义.解决问题的关键是把方程组的解代入原方程组中,求出字母系数.考点2二元一次方程组的解法例2解方程组分析:观察方程组未知数的系数的特点,可以由①得x=1-2y,代入②消去x求解,也可由①+②消元y求解.解法一:(代入法)由①得x=1-2y.③将③代入①,得3(1-2y)-2y=11,解得y=-1.把y=-1代入③,得x=3.所以原方程组的解为解法二:(加减法)①+②,得4x=12,解得x=3.把x=3代入①,得3+2y=1,解得y=-1.所以原方程组的解为点评:解二元一次方程组的关键是消元.求解时一定认真观察并分析方程组中每个未知数的系数特点,灵活确定消元方法,从而降低求解难度.考点3二元一次方程组的应用例3根据以下对话,可以求得小红所买的笔和笔记本的价格分别是()A.0.8元/支,2.6元/本B.0.8元/支,3.6元/本C.1.2元/支,2.6元/本D.1.2元/支,3.6元/本分析:(1)根据两人的对话可得相等关系:①5支笔的费用+10本笔记本的费用=42,②10支笔的费用+5本笔记本的费用=30,根据相等关系列出二元一次方程求解;解:设一支笔的价格为x元,笔记本的价格为y元,根据题意,得由已知条件可知解得故选D.点评:解答这类题的关键是提炼对话所给信息,从对话中找出相等关系,恰当地设出未知数列出二元一次方程组,从而解决了实际问题.例4在课间活动中,小英、小丽和小敏在操场上画出A、B两个区域,一起玩投沙包游戏.沙包落在A区域所得分值与落在B区域所得分值不同.当每人各投沙包四次时,其落点和四次总分如图1所示.请求出小敏的四次总分.图1分析:要想求出小敏的四次总分,需要求出沙包落在A区域所得分值与落在B区域所得分值.设沙包落在A区域得x分,落在B区域得y分,根据小英、小丽的得分图,可以找到两个相等关系,列方程组求解即可.解:设沙包落在A区域得x分,落在B区域得y分,根据题意,得解得所以x+3y=9+3×7=30.哦……我忘了!只记得先后买了两次,第一次买了5支笔和10本笔记本花了42元钱,第二次买了10支笔和5本笔记本花了30元钱.小红,你上周买的笔和笔记本的价格是多少啊?答:小敏的四次总分为30分.点评:本题以“玩投沙包游戏”为背景,取材特别新颖,给学生一种耳目一新的感觉.通过图片中的总分,将这道图片信息问题,抽象出数学问题,建立方程组模型来解答.考查同学们的阅读能力、识图能力和处理信息能力.针对性练习:1.已知方程组的解为,则2a-3b的值为.2.解方程组3.某超市为“开业三周年”举行了店庆活动.对A、B两种商品实行打折出售.打折前,购买5件A商品和1件B商品需用84元;购买6件A商品和3件B商品需用108元.而店庆期间,购买50件A商品和50件B商品仅需960元,这比不打折少花多少钱?参考答案:1.62.3.设打折前A商品的单价为x元,B商品的单价为y元,根据题意,得解得打折前购买50件A商品和50件B商品共需16×50+4×50=1000元.所以打折后少花(1000-960)=40元.答:打折后少花40元.