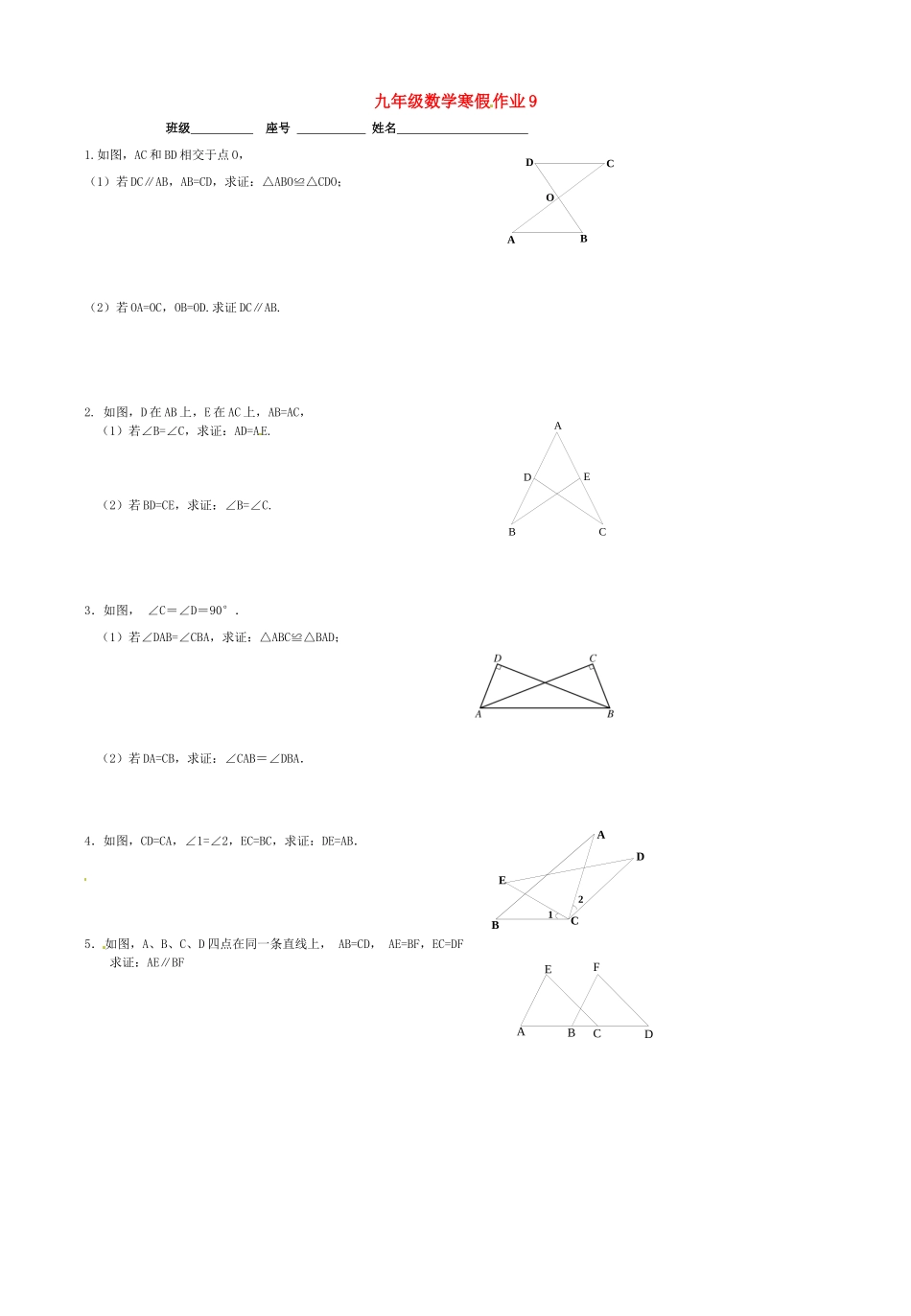
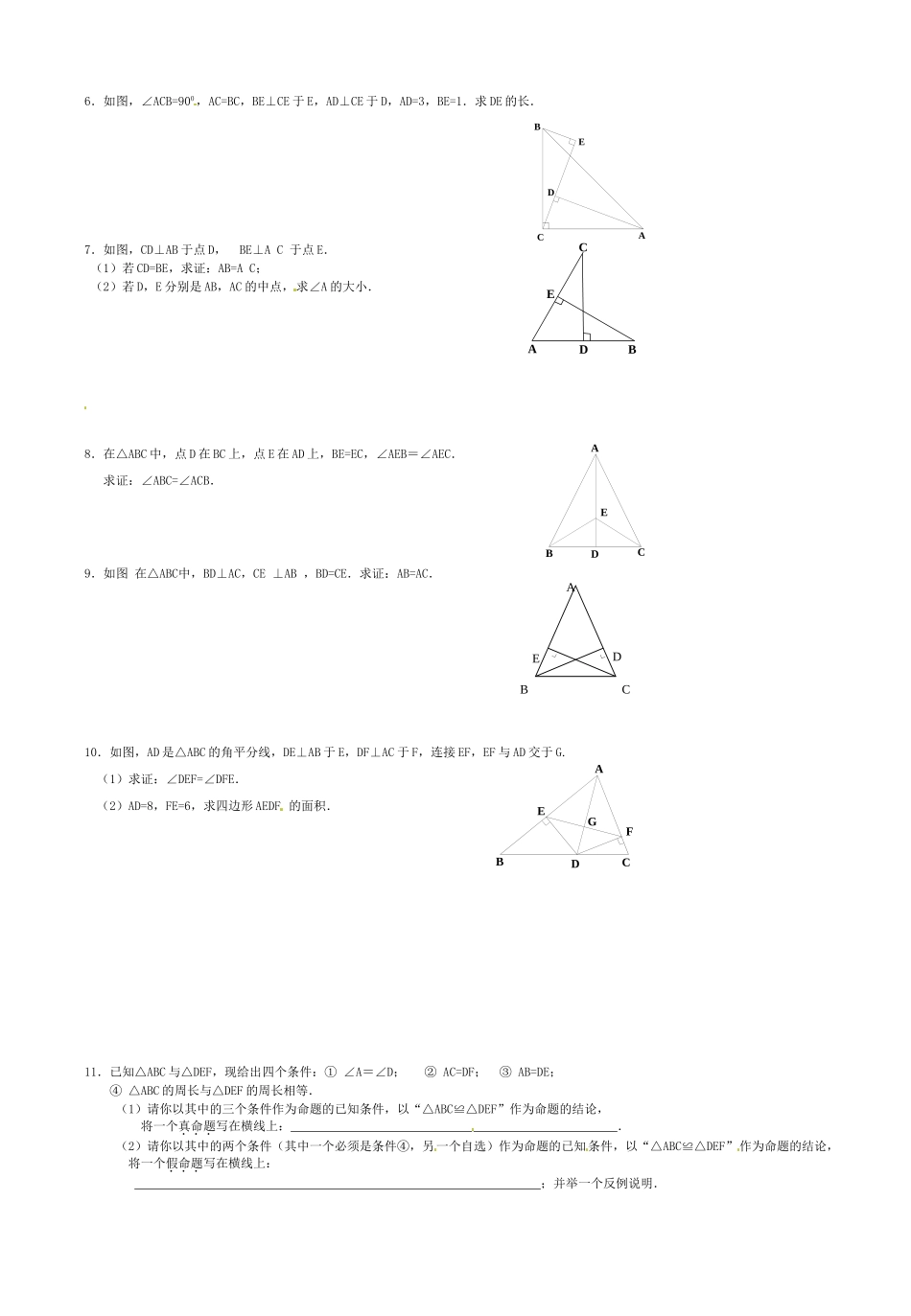
EDCBABCDEFA21EDCBA九年级数学寒假作业9班级座号姓名1.如图,AC和BD相交于点O,(1)若DC∥AB,AB=CD,求证:△ABO≌△CDO;(2)若OA=OC,OB=OD.求证DC∥AB.2.如图,D在AB上,E在AC上,AB=AC,(1)若∠B=∠C,求证:AD=AE.(2)若BD=CE,求证:∠B=∠C.3.如图,∠C=∠D=90°.(1)若∠DAB=∠CBA,求证:△ABC≌△BAD;(2)若DA=CB,求证:∠CAB=∠DBA.4.如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.5.如图,A、B、C、D四点在同一条直线上,AB=CD,AE=BF,EC=DF求证:AE∥BFODCBAEDCBAEDCBAABC∟∟ED6.如图,∠ACB=900,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=3,BE=1.求DE的长.7.如图,CD⊥AB于点D,BE⊥AC于点E.(1)若CD=BE,求证:AB=AC;(2)若D,E分别是AB,AC的中点,求∠A的大小.8.在△ABC中,点D在BC上,点E在AD上,BE=EC,∠AEB=∠AEC.求证:∠ABC=∠ACB.9.如图在△ABC中,BD⊥AC,CE⊥AB,BD=CE.求证:AB=AC.10.如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G.(1)求证:∠DEF=∠DFE.(2)AD=8,FE=6,求四边形AEDF的面积.11.已知△ABC与△DEF,现给出四个条件:①∠A=∠D;②AC=DF;③AB=DE;④△ABC的周长与△DEF的周长相等.(1)请你以其中的三个条件作为命题的已知条件,以“△ABC≌△DEF”作为命题的结论,将一个真命题写在横线上:.(2)请你以其中的两个条件(其中一个必须是条件④,另一个自选)作为命题的已知条件,以“△ABC≌△DEF”作为命题的结论,将一个假命题写在横线上:;并举一个反例说明.EDCBAGEFDCBAABCDE12.如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF⊥AG于F.(1)线段DE、EF、BF之间有何关系,说明理由;(2)当点G在BC上的延长线上时,(2)中线段DE、EF、BF之间的关系仍然成立吗?若成立,请加以证明;若不成立,请写出线段DE、EF、BF之间的关系.(请画出图形,不加证明)13.如图,在直角梯形ABCD中,AB∥CD,∠B=90°,E是BC上的一点,连结AE,DE,且AE=DE,∠AED=90°.(1)求证:△ABE≌△ECD;(2)若△AED的面积是225,直角梯形ABCD的面积是249,求△ABE的周长;(3)若△AED的面积是a,直角梯形ABCD的面积是b,试判断b与a2的大小,并说明理由.DCBAEFG