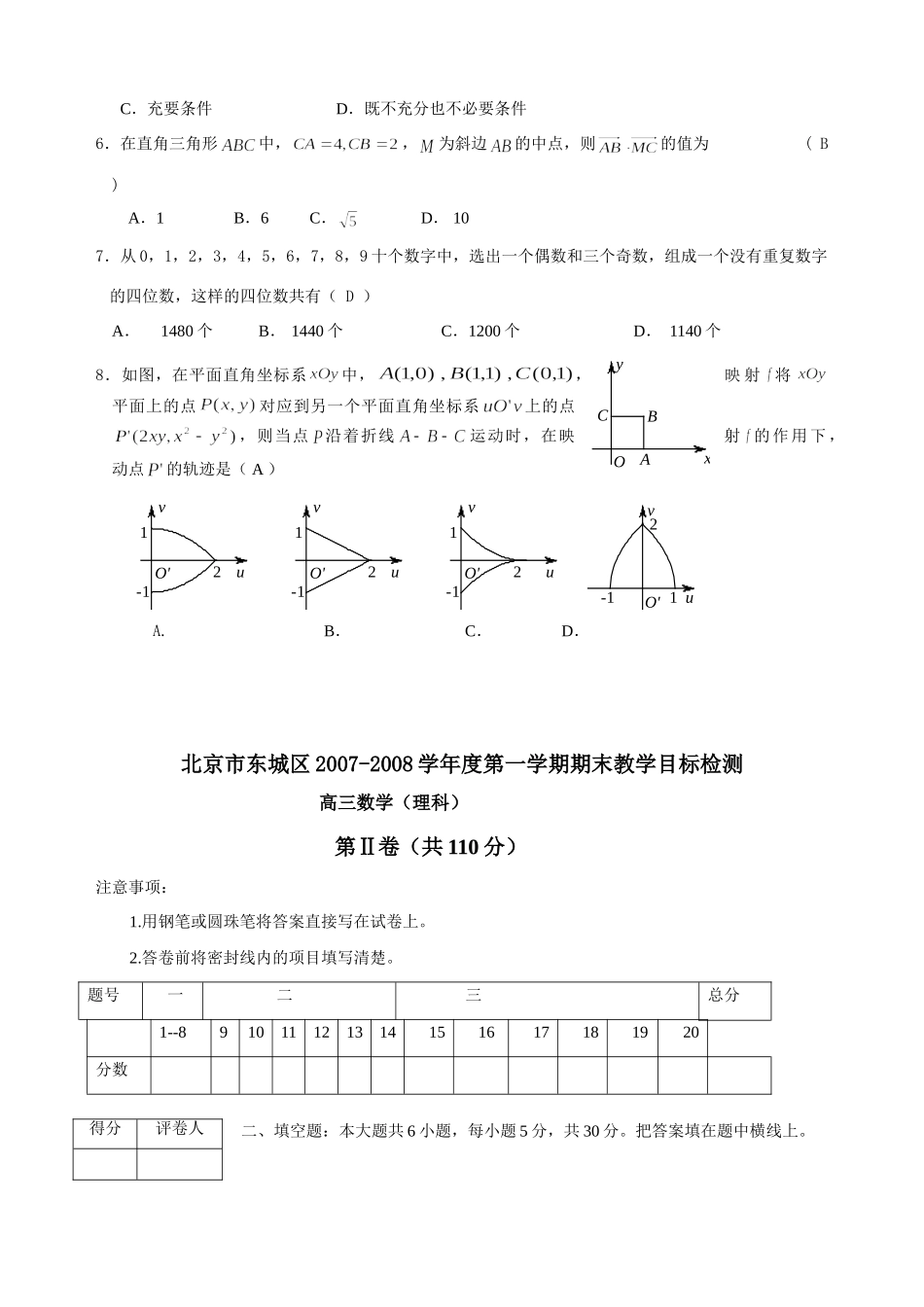
北京市东城区2007-2008学年度第一学期期末教学目标检测高三数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟。考试结束,将本试卷和答题卡一并交回。第Ⅰ卷(选择题共40分)注意事项:1、答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试卷上。一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,选出符合题目要求的一项。1.已知集合,则等于(B)A.B.C.D.2.的值为(C)A.0B.1C.D.3.已知两个不同的平面,和两条不重合的直线,,有下列四个命题:①若,则②若,且,则③若,则④若,,则其中正确命题的个数是(A)A.1个B.2个C.3个D.4个4.的展开式中含项的系数是(D)A.240B.C.192D.5.已知数列,那么“对任意的点都在直线上”是“为等差数列”的(A)A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件6.在直角三角形中,,为斜边的中点,则的值为(B)A.1B.6C.D.107.从0,1,2,3,4,5,6,7,8,9十个数字中,选出一个偶数和三个奇数,组成一个没有重复数字的四位数,这样的四位数共有(D)A.1480个B.1440个C.1200个D.1140个8.如图,在平面直角坐标系中,,映射将平面上的点对应到另一个平面直角坐标系上的点,则当点沿着折线运动时,在映射的作用下,动点的轨迹是(A)O'uv21-1O'uv21-1O'uv21-1O'uv21-1A.B.C.D.北京市东城区2007-2008学年度第一学期期末教学目标检测高三数学(理科)第Ⅱ卷(共110分)注意事项:1.用钢笔或圆珠笔将答案直接写在试卷上。2.答卷前将密封线内的项目填写清楚。题号一二三总分1--891011121314151617181920分数二、填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。得分评卷人OxyABCABMCDA1B1C1D19.已知函数,它的反函数为,则=.10.离心率的椭圆,它的焦点与双曲线的焦点重合,则此椭圆的方程为.若为该椭圆上一点,且到椭圆一个焦点的距离为3,则到椭圆相应准线的距离为.11.如图,棱长为的正方体中,为中点,则直线与平面所成角的正切值为;若正方体的八个顶点都在同一球面上,则此球的表面积为.12.已知数列是公差为的等差数列,且,数列是公比为的等比数列,且,则,.13.已知中,,则的最大值为.14.已知符号函数,则不等式的解集是.三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。15.(本小题满分13分)已知函数.(Ⅰ)求的值;(Ⅱ)求的最大值并指出相应的的取值集合.16.(本小题满分13分)已知函数的图象过点,且在点处的切线的方程为.得分评卷人得分评卷人(Ⅰ)求的值;(Ⅱ)求函数的单调区间;(Ⅲ)求函数的最值.17.(本小题满分14分)如图,四棱锥中,底面是边长为2的正方形,,且,为中点.(Ⅰ)求证:平面;(Ⅱ)求二面角的大小;(Ⅲ)在线段上是否存在点,使得点到平面的距离为?若存在,确定点的位置;若不存在,请说明理由.18.(本小题满分13分)有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为.(Ⅰ)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;(Ⅱ)若四名运动员每两人之间进行一场比赛,求甲恰好胜两场的概率;(Ⅲ)若四名运动员每两人之间进行一场比赛,设甲获胜场次为,求随机变量的分布列及期望.19.(本小题满分13分)已知抛物线,过焦点的动直线交抛物线于两点,抛物线在两点处得分评卷人得分评卷人得分评卷人PABCDE的切线相交于点.(Ⅰ)求的值;(Ⅱ)求点的纵坐标;(Ⅲ)证明:.20.(本小题满分14分)已知数列满足:.数列满足:,,数列的前n项和为.(Ⅰ)求证:数列为等差数列;(Ⅱ)求证:数列为等比数列;(Ⅲ)若当且仅当时,取得最小值,求的取值范围.北京市东城区2007-2008学年度第一学期期末教学目标检测高三数学参考答案(理科)一、选择题(本大题共8小题,每小题5分,共40分)...