宁夏银川市届九年级数学上学期期中考试试卷 新人教版试卷VIP免费

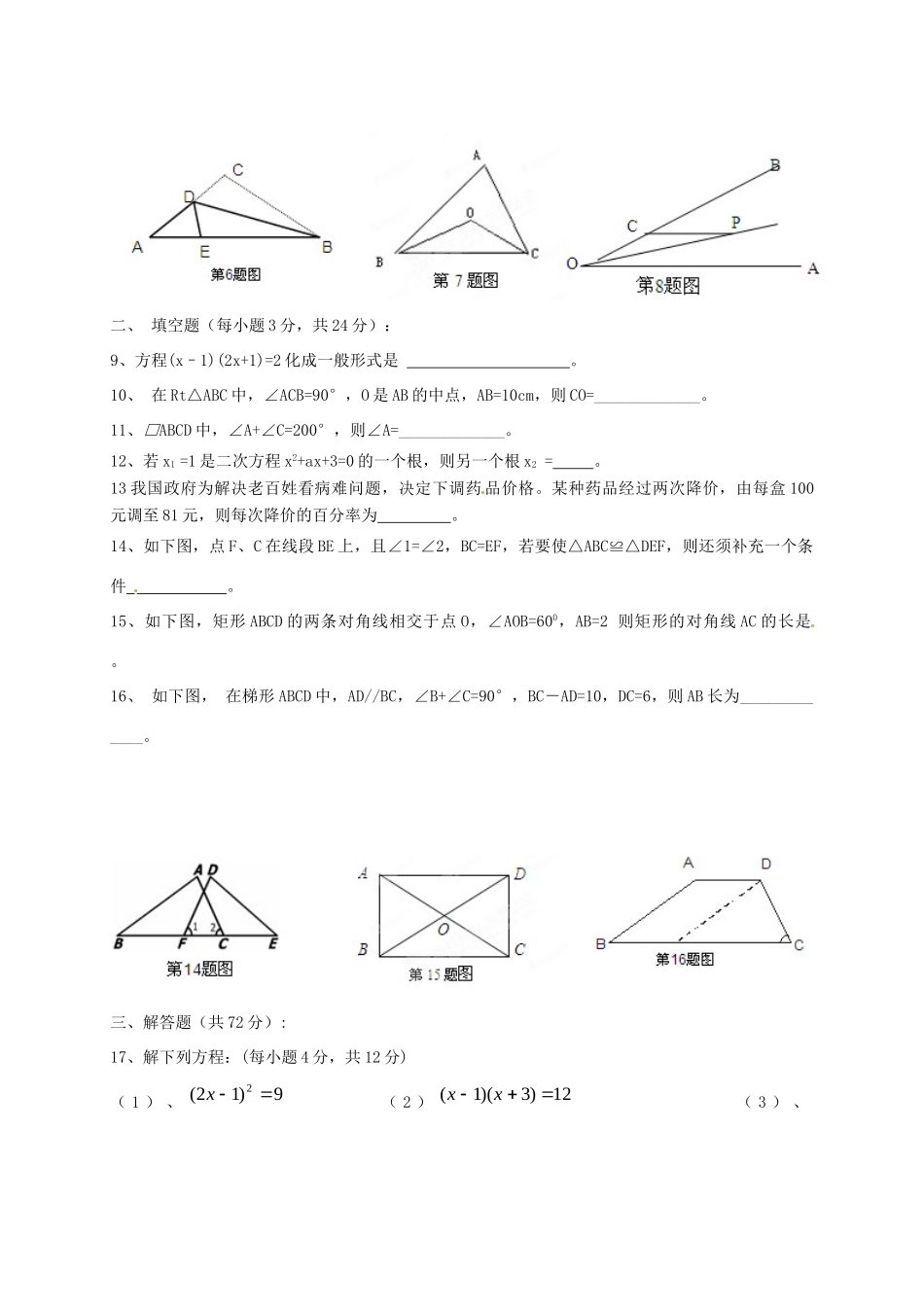
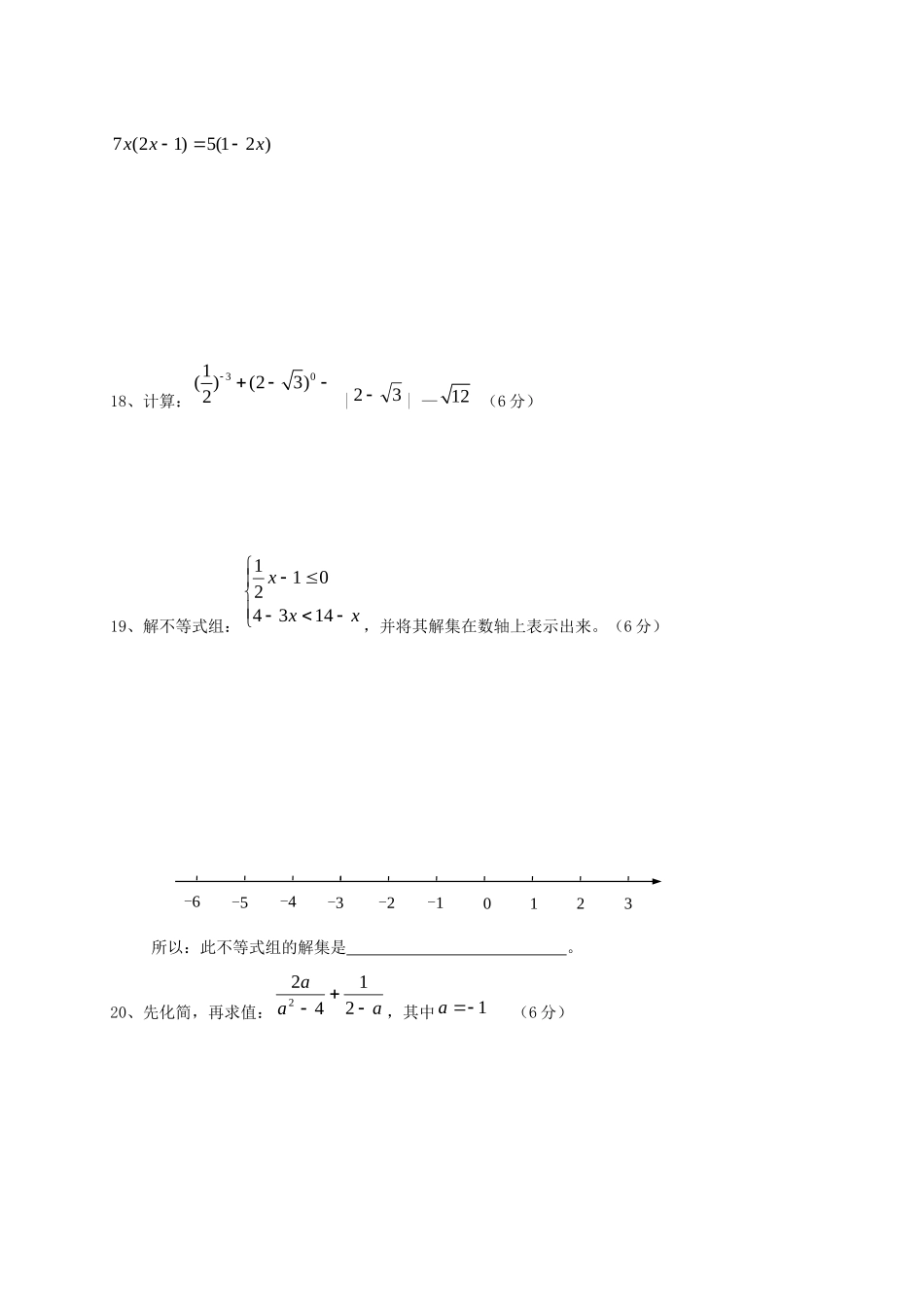
宁夏银川市2013届九年级数学上学期期中考试试题（无答案）新人教版（总分：120分时间：120分钟）一、选择题（每小题3分，共24分）：1、一元二次方程x2-1=0的根为（）A.x＝1B.x＝－1C.x1＝1，x2＝－1D.x1＝0，x2＝12、如果(m+3)x2-mx+1=0是关于x的一元二次方程，则()A、3mB、3mC、0mD、03mm且3、下列长度的三条线段①8，15，17②4，5，6③24，25，7④5，8，10其中能构成直角三角形的是（）A.①②B.①③C.①④D.③④4、下列方程中一定有两个不相等实数根的是（）A.032xB.022xxC.0232xxD.02022xx5、下列图形中既是中心对称图形，又是轴对称图形的是（）A.矩形B.平行四边形C.正三角形D.等腰梯形6、如下图，三角形纸片ABC，cmAB10,cmBC7,cmAC6，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）A.9cmB.13cmC.16cmD.10cm7、如下图在△ABC中，点O是∠ABC与∠ACB的角平分线的交点，若∠BAC=800，则∠BOC的度数是（）A、1300B、1000C、650D、5008、如下图，OP平分∠BOA，∠BOA=30°，PC∥OA，若PC=4，则点P到OA的距离是()A.4B.22C.32D.2二、填空题（每小题3分，共24分）：9、方程(x–1)(2x+1)=2化成一般形式是。10、在Rt△ABC中，∠ACB=90°，O是AB的中点，AB=10cm，则CO=_____________。11、□ABCD中，∠A+∠C=200°，则∠A=_____________。12、若x1=1是二次方程x2+ax+3=0的一个根，则另一个根x2=。13我国政府为解决老百姓看病难问题，决定下调药品价格。某种药品经过两次降价，由每盒100元调至81元，则每次降价的百分率为。14、如下图，点F、C在线段BE上，且∠1=∠2，BC=EF，若要使△ABC≌△DEF，则还须补充一个条件。15、如下图，矩形ABCD的两条对角线相交于点O，∠AOB=600，AB=2则矩形的对角线AC的长是。16、如下图，在梯形ABCD中，AD//BC，∠B+∠C=90°，BC－AD=10，DC=6，则AB长为_____________。三、解答题（共72分）:17、解下列方程：(每小题4分，共12分)（1）、9)12(2x（2）12)3)(1(xx（3）、)21(5)12(7xxx18、计算：301()(23)2|32|—12（6分）19、解不等式组：xxx14340121，并将其解集在数轴上表示出来。（6分）所以：此不等式组的解集是。20、先化简，再求值：aaa21422，其中1a（6分）0123-1-2-3-4-5-621、某小区规划在一个长10m，宽8m的矩形场地ABCD上修建三条同样宽的道路，使其中两条与AB平行，另一条与AD平行，如图，其余部分种草，若每块种草面积达到6m2，求道路的宽。（6分）22、某商店将某商品按每件2元的利润售出，每天可销售200件，现在采用提高商品售价减少销售量的办法增加利润，如果这种商品按每件的销售价每提高1元，其销售量就减少20件，为了尽可能的使消费者得到实惠，问应将每件售价定为多少元时，才能使每天利润为640元？（6分）23、如图，已知AB⊥BD，CD⊥BD,点E、F在BC上，AF，CE相交于点O，AF=CE，BE=DF，求证：（1）△ABF≌△CDE（3分）（2）OE=OF（3分）24、已知：点P是□ABCD的对角线AC的中点，经过点P的直线EF交AB于点E，交DC于点F．求证：AE=CF．（7分）25、已知：如图，等腰三角形ABC中，AC＝BC，∠ACB＝90°，直线l经过点C(点A、B都在直线l的同侧)，AD⊥l，BE⊥l，垂足分别为D、E．求证：△ADC≌△CEB.（7分）26、如图，在△ABC中，AB=AC，点D是BC的中点，作AE//BC，CE//AD，AE、CE交于点E。（1）证明四边形ADCE是矩形。（4分）（2）若DE交AC于点O，证明：OD//AB且OD=21AB。（4分）（3）若使四边形ADCE是正方形，那么△ABC需添加一个条件(请直接写出该条件)。（2分）