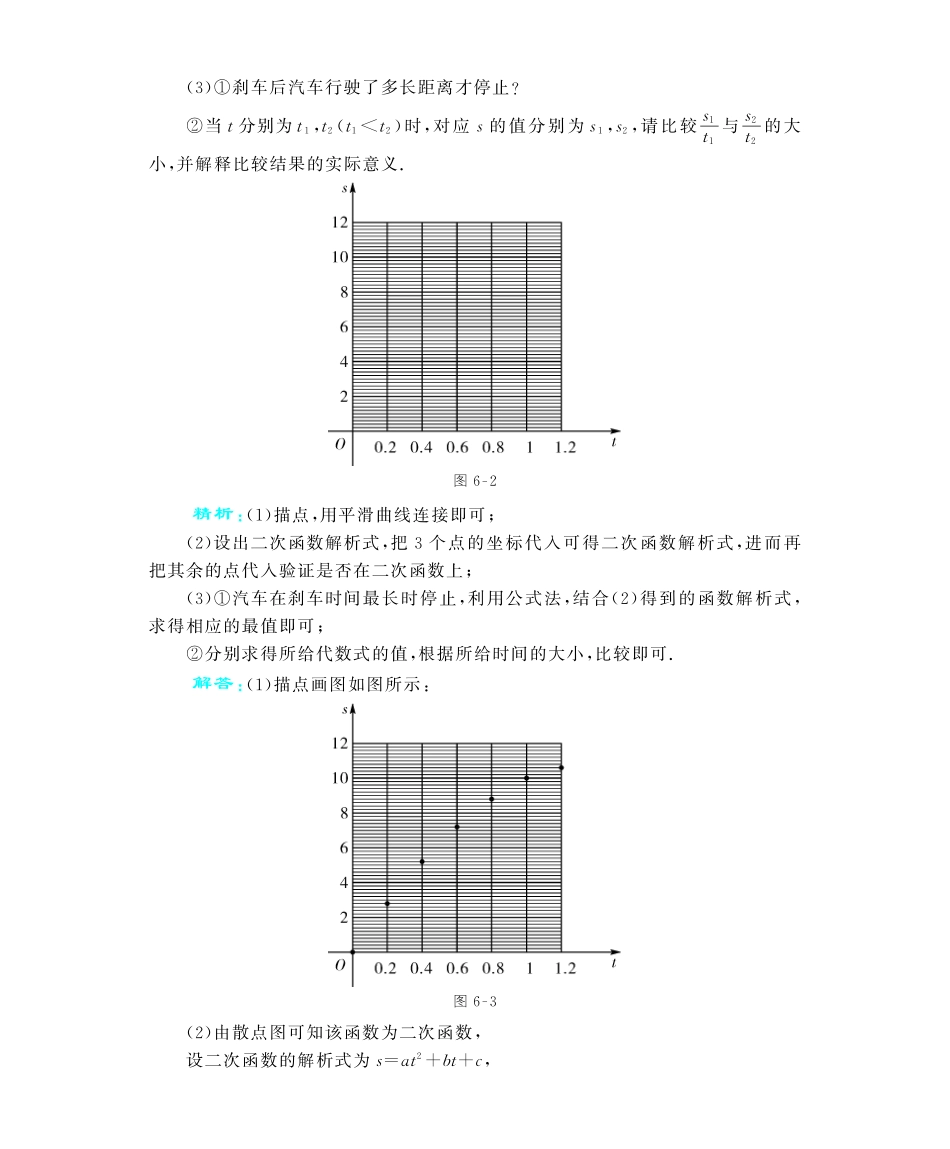
知识结构串联中考专题透析专题1确定二次函数的关系式,体会二次函数的意义.命题热点趋向:确定二次函数的关系式是运用函数解决问题的基本要求.通过对问题(数学问题或实际问题)的分析,先确定函数的关系式,然后利用二次函数的性质解决问题,这是中考试题常见的命题思路.解题思路梳理:确定二次函数的关系式有两种情形,一是根据实际问题中基本量之间的数量关系,经整理得到函数关系式;一是由二次函数图象上三个点的坐标,运用待定系数法即通过列三元一次方程组,确定二次项系数、一次项系数及常数项.例1(2011重庆江津)已知双曲线y=kx与抛物线y=ax2+bx+c交于A(2,3),B(m,2),C(-3,n)三点.(1)求双曲线与抛物线的解析式;(2)在平面直角坐标系中描出点A、B、C,并求出△ABC的面积.(1)(2)图6G1精析:根据双曲线过点A,将点A的坐标代入方程便可求出未知数k,进而可确定B、C两点的坐标,求出a,b,c的值.解答:(1)把点A(2,3)代入y=kx,得k=6.∴反比例函数的解析式为y=6x.把点B(m,2),C(-3,n)分别代入y=6x,得m=3,n=-2.把A(2,3),B(3,2),C(-3,-2)分别代入y=ax2+bx+c,得4a+2b+c=3,9a+3b+c=2,9a-3b+c=-2.{解得a=-13,b=23,c=3.ìîíïïïïï∴抛物线的解析式为y=-13x2+23x+3.(2)描点画图如图(2)所示.S△ABC=12(1+6)×5-12×1×1-12×6×4=352-12-12=5.专题2用描点法画出二次函数的图象.命题热点趋向:考查二次函数往往涉及到它的图象,因为通过图象可以较直观的揭示二次函数的性质,并结合图象解决问题,体会数形结合的数学思想.试题常以解答题形式呈现,先描点画出函数的图象,在此基础上确定函数的关系式,再综合运用相关有联系的知识解决问题.解题思路梳理:根据题意,先描点画出函数的图象,通过图象的形状,可以初步判断所列出的函数是哪一类函数,然后进一步验证,确认此函数为二次函数后,再运用其性质解决问题.由于二次函数的图象是轴对称图形,所以在描点、连线时要给予关注.例2(2012浙江台州)某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:时间t(秒)00.20.40.60.81.01.2行驶距离s(米)02.85.27.28.81010.8(1)根据这些数据在给出的坐标系中画出相应的点;(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;(3)①刹车后汽车行驶了多长距离才停止?②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较s1t1与s2t2的大小,并解释比较结果的实际意义.图6G2精析:(1)描点,用平滑曲线连接即可;(2)设出二次函数解析式,把3个点的坐标代入可得二次函数解析式,进而再把其余的点代入验证是否在二次函数上;(3)①汽车在刹车时间最长时停止,利用公式法,结合(2)得到的函数解析式,求得相应的最值即可;②分别求得所给代数式的值,根据所给时间的大小,比较即可.解答:(1)描点画图如图所示:图6G3(2)由散点图可知该函数为二次函数,设二次函数的解析式为s=at2+bt+c, 抛物线经过点(0,0),∴c=0.又由点(0.2,2.8),(1,10),得0.04a+0.2b=2.8,a+b=10,{解得a=-5,b=15.∴二次函数的解析式为s=-5t2+15t.经检验,其余点均在s=-5t2+15t上.(3)①汽车刹车后到停止时的距离即汽车滑行的最大距离,当t=-152×(-5)=32时,滑行距离最大,s=0-1524×(-5)=22520=454,即刹车后汽车行驶了454米才停止.② s=-5t2+15t,∴s1=-5t21+15t1,s2=-5t22+15t2.∴s1t1=-5t21+15t1t1=-5t1+15.同理s2t2=-5t2+15,∴t1<t2.∴s1t1>s2t2.其实际意义是刹车后到t2时间内的平均速度小于刹车后到t1时间内的平均速度.点拨:考查二次函数的应用;结合实际意义比较刹车时的平均速度的大小是解决本题的难点.例3(2012山东济南)如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是().图6G4A.y的最大值...