安徽省合肥市高三数学第一次教学质量检测试卷理新人教A版试卷VIP免费

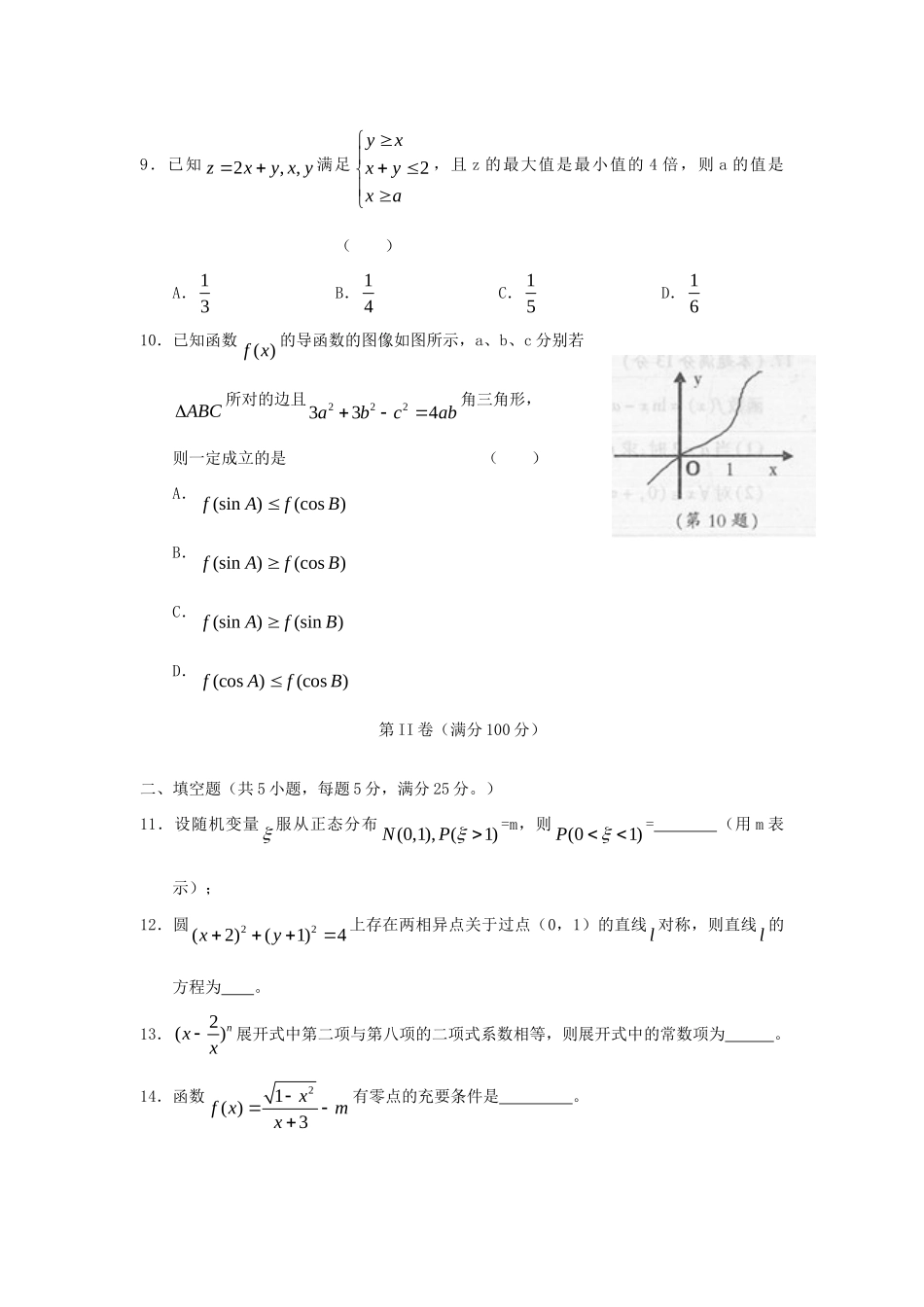
安徽省合肥市2012年高三第一次教学质量检测数学试题（理）考试时间：120分钟满分：150分注意事项：1．答题前，务务在答题卷、答题卡规定的地方填写自己的姓名、座位号和座位号后两位。2．答第I卷时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。3．答第II卷时，必须使用0.5毫米的黑色墨水签字笔在答题卡上书写，要求字体工整、笔迹清晰，作图题可先用铅笔在答题卡规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚。必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效。4．考试结束，务必将么将答题卡和答题卷一并上交。第I卷（满分50分）一、选择题（共10个小题，每小题5分，满分5分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．复数11zi（i为虚数单位）的共轭复数z是（）A．1-iB．1+iC．1122iD．1122i2．集合{|220}AxRx，2{|20}BxRxx，则()RACB=（）A．（-1，2）B．[-1，2]C．（0，2）D．0,23．与椭圆2211216xy是有共焦点，且离心率互为倒数的双曲线方程是（）A．2213xyB．2213yxC．2233148xyD．2233148yx4．某一几何体的三视图如图所示，则该几何体的表面积为（）A．54B．58C．60D．635．已知α为锐角，4sin5，则tan()4=（）A．17B．17C．-7D．76．已知数列{}na满足*111,2()nnnaaanN，则2012S=（）A．201221B．1006323C．1006321D．10053227．如图所示的程序框图运行的结果是（）A．12012B．12013C．20112012D．201220138．建立从集合{1,2,3,4}A到集合{5,6,7}B的所有函数，从中随机抽取一个函数，则其值域是B的概率为（）A．916B．316C．49D．899．已知2,,zxyxy满足2yxxyxa，且z的最大值是最小值的4倍，则a的值是（）A．13B．14C．15D．1610．已知函数()fx的导函数的图像如图所示，a、b、c分别若ABC所对的边且222334abcab角三角形，则一定成立的是（）A．(sin)(cos)fAfBB．(sin)(cos)fAfBC．(sin)(sin)fAfBD．(cos)(cos)fAfB第II卷（满分100分）二、填空题（共5小题，每题5分，满分25分。）11．设随机变量服从正态分布(0,1),(1)NP=m，则(01)P=（用m表示）；12．圆22(2)(1)4xy上存在两相异点关于过点（0，1）的直线l对称，则直线l的方程为。13．2()nxx展开式中第二项与第八项的二项式系数相等，则展开式中的常数项为。14．函数21()3xfxmx有零点的充要条件是。15．若函数()|sin|fxx的图象与直线ykx仅有三个公共点，且其横坐标分别为α，β，()，给出下列结论：①cosk；②3(,)2；③tan；④22sin21其中正确的是（填上所有正确的序号）三、解答题（共6小题，满分75分）16．（本题满分12分）函数2()sincoscos.fxxxx（1）求()fx的最小正周期和在[0,]2上的最大值及最小值；（2）若A为ABC的内角，若()12Af，判断ABC的形状。17．（本题满分13分）某篮球队在一场比赛中，11名队员得分情况如下：2457891314152123（1）请设计适当的茎叶图表示该组数据；（2）计算该队队员在本场比赛中得分的平均值；（3）从上述得分超过10分的队员中任取2人，记选取2人中得分超过20分的人数为，求的分布列和数学期望。18．（本题满分12分）（本题满分12分）如图，在多面体ABC—A1B1C1中，1AA平面ABC，11//AABB，11121,//.22ABACAABCBCBC（1）求证：11AB平面AA1C；（2）求证：AB1//平面A1C1C；（3）求二面角C1—A1C—A的余弦值。19．（本题满分12分）已知等差数列{}na的前n项和为159,6,63.nAaaA（1）求数列{}na的通项公式na及前n项和;nA（2）数列{}nb的前n项和nB满足：*681,()nnBbnN，数列{}nnab的前n项和为nS，求证：1.48nnS20．（本题满分13分）已知函数()ln.xxx（1）求函数()yfx的单调区间和极值；（2）若函数()()ln(02)ygxfxxxx与关于点（1，0）对称，证明：当02x时，()().fxgx21．（本题满分14分）已知向量(22,23),(32,1)mxynyx，且//,(,)mnOMxy�（O为坐标原点）。（1）求点M的轨迹C的方程；（2）是否存在过点F（1，0）的直线l与曲线C相交于A、B两点，并且曲线C存在点P，使四边形OAPB为平行四边形？若存在，求出平行四边形OAPB的面积；若不存在，说明理由。