九年级数学9月月考试卷 北京课改版试卷VIP免费

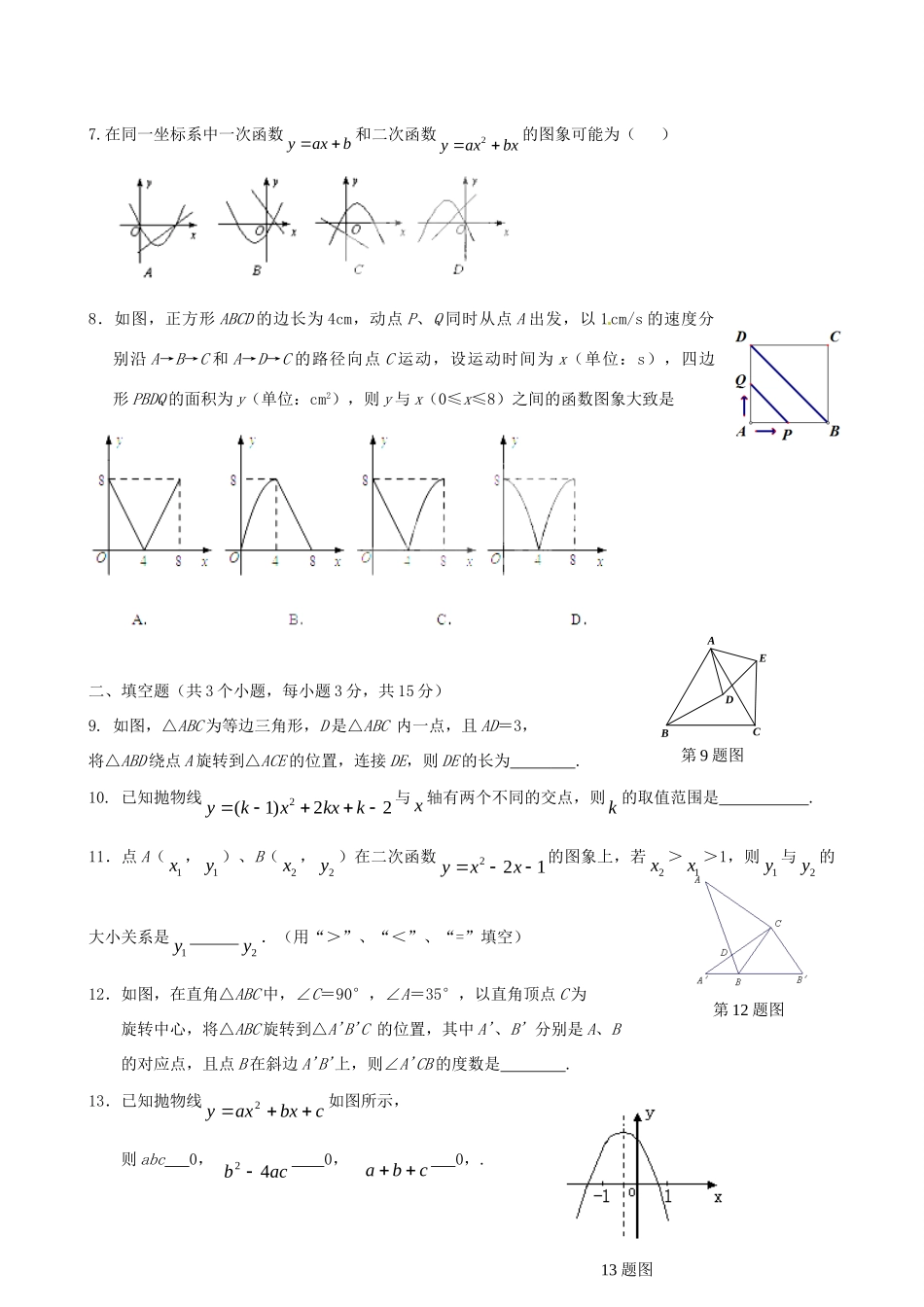
北京市楼梓庄中学2015届九年级数学9月月考试题（考试时间90分钟满分100分）学校班级姓名考号一、选择题（共8个小题，每小题3分，共24分）下列各题均有四个选项，其中只有一个是符合题意的．1.下列图形是中心对称图形的是（）A.B.C.D.2.已知x=1是一元二次方程0122mxx的一个解，则m的值是（）A.1B.0C.0或1D.0或-13.一元二次方程032xx的解为（）A．3xB．01x，32xC．01x，32xD．11x，32x4.抛物线1)2(2xy是由抛物线2xy平移得到的，下列对于抛物线2xy的平移过程叙述正确的是（）A．先向右平移2个单位，再向上平移1个单位B．先向右平移2个单位，再向下平移1个单位C．先向左平移2个单位，再向上平移1个单位D．先向左平移2个单位，再向下平移1个单位5.二次函数221yxx与x轴的交点个数是（）A．0B．1C．2D．36.将抛物线3)1(22xy关于y轴对称，得到的抛物线是A．22(1)3yxB．22(1)3yxC．22(1)3yxD．22(1)3yx第12题图13题图7.在同一坐标系中一次函数yaxb和二次函数2yaxbx的图象可能为（）8．如图，正方形ABCD的边长为4cm，动点P、Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动，设运动时间为x（单位：s），四边形PBDQ的面积为y（单位：cm2），则y与x（0≤x≤8）之间的函数图象大致是二、填空题（共3个小题，每小题3分，共15分）9.如图，△ABC为等边三角形，D是△ABC内一点，且AD＝3，将△ABD绕点A旋转到△ACE的位置，连接DE，则DE的长为.10.已知抛物线2(1)22ykxkxk与x轴有两个不同的交点，则k的取值范围是.11．点A（1x，1y）、B（2x，2y）在二次函数221yxx的图象上，若2x＞1x＞1，则1y与2y的大小关系是1y2y．（用“＞”、“＜”、“=”填空）12．如图，在直角△ABC中，∠C＝90°，∠A＝35°，以直角顶点C为旋转中心，将△ABC旋转到△A'B'C的位置，其中A'、B'分别是A、B的对应点，且点B在斜边A'B'上，则∠A'CB的度数是.13．已知抛物线cbxaxy2如图所示，则abc0，acb420，cba0，.ECBAD第9题图第15题图三、解答题（本小题12分）14.（本小题满分12分）（1）解方程：0742xx（要求：用配方法）．（2）解方程：0)1(232xx.(3)解方程：x－2=x（x－2）四、作图题15．（本小题满分4分）如图，在每个小正方形的边长均为1个单位长度的方格纸中，△ABO的顶点均与小正方形的顶点重合．以点O为坐标原点建立平面直角坐标系后，点A的坐标为（－2，4）．（1）在方格纸中，将△ABO绕点O逆时针旋转90°，得到△A1B1O，请你画出△A1B1O；（2）在方格纸中，画出与△ABO关于原点中心对称的图形.五、解答题（共7个小题，共45分）16.（本小题满分5分）已知关于x的一元二次方程．)1(0222kkxkx（1）求证：方程总有两个实数根；（2）当k取哪些整数时方程的两根均为整数．17.（本小题满分6分）二次函数2yaxbxc的部分图象如图所示，其中图象与x轴交于点A（－1,0），与y轴交于点C（0，－5），且经过点D（3，－8）.（1）求此二次函数的解析式；17题图（2）直接写出此二次函数图象的顶点坐标和与坐标轴的交点坐标；第18题图A18.（本小题满分5分）如图，已知抛物线y1=-x2+bx+c经过A(1,0)，B(0,-2)两点，顶点为D．（1）求抛物线y1的解析式；（2）将△AOB绕点A顺时针旋转90°后，得到△AO′B′，将抛物线y1沿对称轴平移后经过点B′，求出平移后所得的抛物线y2的解析式.19.（本小题满分6分）为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）.若设绿化带的BC边长为xm，绿化带的面积为ym².（1）求y与x之间的函数关系式，并写出自变量x的取值范围；（2）当x为何值时，满足条件的绿化带的面积最大？最大面积为多少？20．（本小题满分6分）二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，根据图象解答下列问题：（1）写出x为何值时，y的值大于0；（2）写出x为何值时，y随x的增大而增大；（3）若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围．解：（1）20题图C_25m19...