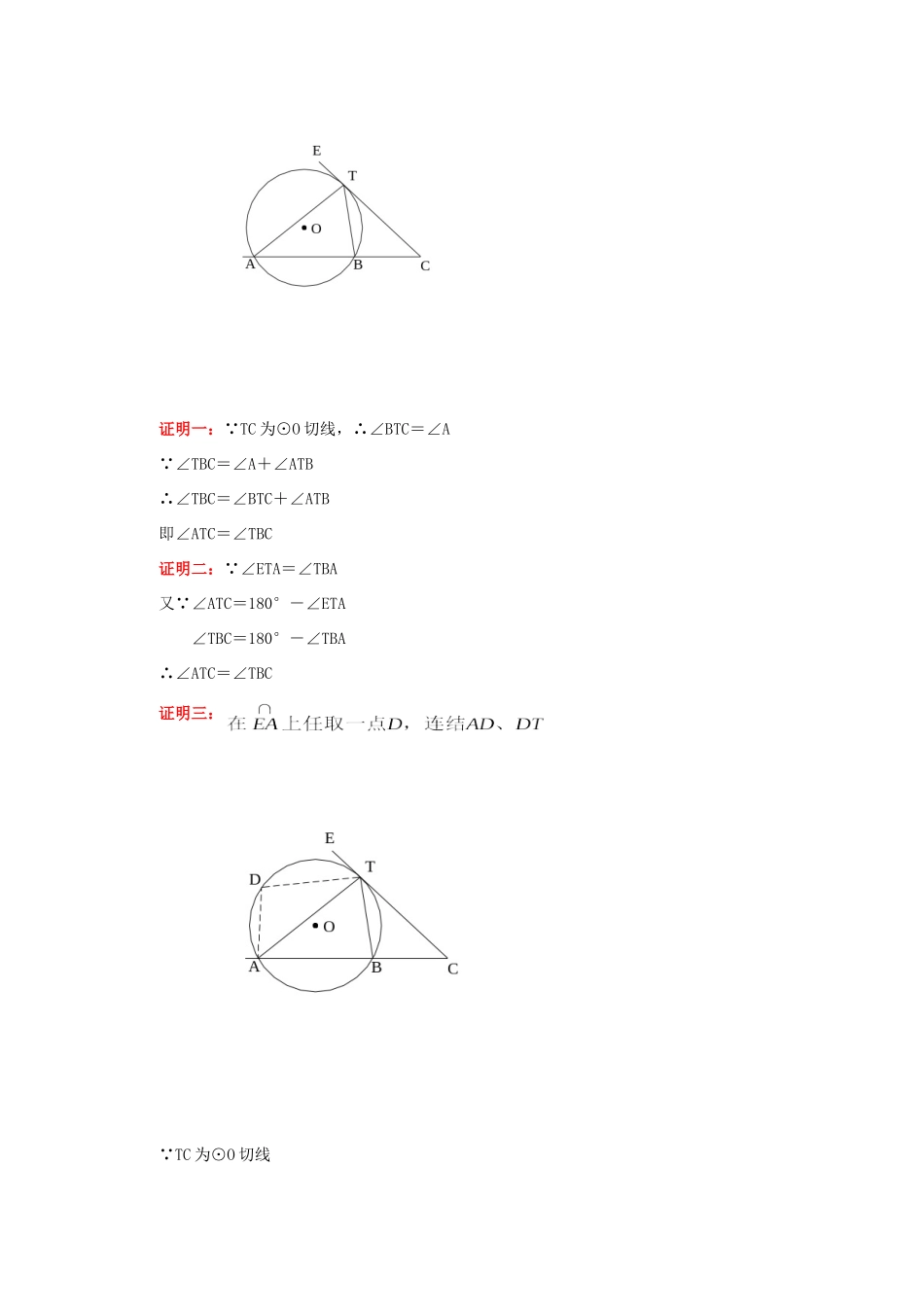
初三数学弦切角及和圆有关的比例线段知识精讲一.本周教学内容:弦切角及和圆有关的比例线段二.重点、难点:1.弦切角的概念:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。注意:弦切角必须具备三个条件:(1)顶点在圆上(切点),(2)一边和圆相切,(3)一边和圆相交(弦),三者缺一不可。2.弦切角定理:弦切角等于它所夹的弧对的圆周角。3.弦切角定理的推论:如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。弦切角是和圆有关的角之一,其他几种有圆心角、圆周角、圆内接四边形的外角。这四种角之间的关系及转换是与圆有关的论证及计算的基础。4.相交弦定理:圆内两条相交弦,被交点分成的两条线段长的积相等。5.相交弦定理的推论:如果弦与直径相交,那么弦的一半是它分直径所成的两条线段的比例中项。6.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。7.切割线定理的推论(或称割线定理):从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。本节是本章中综合性最强的部分,是本章及初中平面几何中难点之一。其中,相交弦定理、切割线定理及割线定理在证明等积式、比例式和线段长度的计算中起着极其重要的作用。这三个定理实际是一个整体,可以看做相交弦交点从圆内移到圆外,由割线旋转到切线时的结果。应用定理和推论解题时,要注意数形结合的思想、方程思想的运用。由于定理和推论的结论都是两条线段乘积的形式,所以一元二次方程更显威力。例1.如图,经过⊙O上的点T的切线和弦AB的延长线相交于点C。求证:∠ATC=∠TBC证明一: TC为⊙O切线,∴∠BTC=∠A ∠TBC=∠A+∠ATB∴∠TBC=∠BTC+∠ATB即∠ATC=∠TBC证明二: ∠ETA=∠TBA又 ∠ATC=180°-∠ETA∠TBC=180°-∠TBA∴∠ATC=∠TBC证明三: TC为⊙O切线∴∠ATC=∠D 圆内接四边形ABTD∴∠TBC=∠D∴∠ATC=∠TBC例2.已知:如图,AB是⊙O的弦,P是AB上的一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径。解析:由P为AB上的一点,且由已知PA、PB,故联想到相交弦定理,所以需把OP向两方延长,分别与圆相交,再利用相交弦定理解之。解:向两方延长OP,分别交⊙O于C、D由相交弦定理有:BP·AP=CP·DP又 CP=CO+OP,DP=OD-OP,CO=DO答:⊙O半径为7cm。此题还可以利用垂径定理、勾股定理求解,过O点作OD⊥AB于D,连结OB,则DP=1,BD=5,,与上面方法比较繁一些。例3.如图,△ABC内接于⊙O,PA切⊙O于A,过BC的中点D作割线PGF交AB于E,且AC//PF。(1)求证:AE2=PE·DE;(2)若AE=4,PE=5,EF=8,求PA的长。(1)证明: PA是⊙O切线,∴∠PAB=∠C PF//AC,∴∠C=∠PDB,∴∠PAB=∠PDB(2)解:根据相交弦定理:AE·BE=GE·EF PA是⊙O的切线例4.AB是半圆O的直径,C是AB延长线上一点,CD切半圆于D,连结AD,若AD=15,,求BC的长。分析:由于,因此要把∠C放在直角三角形中使用,连结OD,可以利用切线性质得到Rt△ODC,于是切线长CD,半径OD及OC的比值就可求出了。连结DB,利用切割线的比求出AD、DB的比值,又可用Rt△ADB,求出AB的长度。解:连结OD、DB CD是⊙O切线,∴OD⊥CD AB是⊙O直径注意:将Rt△ADB中,DB、AD两边的比转化为切线、割线的比,例5.如图,P是⊙O直径CB延长线上的点,PA切⊙O于A,PA=15,PB=5,弦AD交CB于点M。(1)若MA2=MB·MP,试判断CD与AP是否平行,并说明理由。(2)求弦AC的长。(3)当点D在⊙O上运动时,可以得到△ACD的最大面积,请计算这个最大面积。(1)CD//AP证明:连结AB(2)解: PA是⊙O的切线,PBC是⊙O的割线(3)由(2)可知,在△ACD中,AC是定值∴点D到AC的距离最大时,△ACD的面积最大此时△ACD的面积最大此题用了圆中的不少知识、概念,综合性较强。例6.已知:如图,AB是⊙O直径,C为半圆的三等分点,PB、PC分别切⊙O于C,且AB=14,PA交⊙O于点D,DE//PB交AB于点F,交⊙O于点E。(1)求AD的长;(2)求tan∠AED。解:(1)连结BC、AC AB是直径,∴∠ACB=90°(2) DE∥PB,AB⊥BP∴DE⊥AB于F AB是⊙O直径例7.已知:如图,AB为⊙O直径...