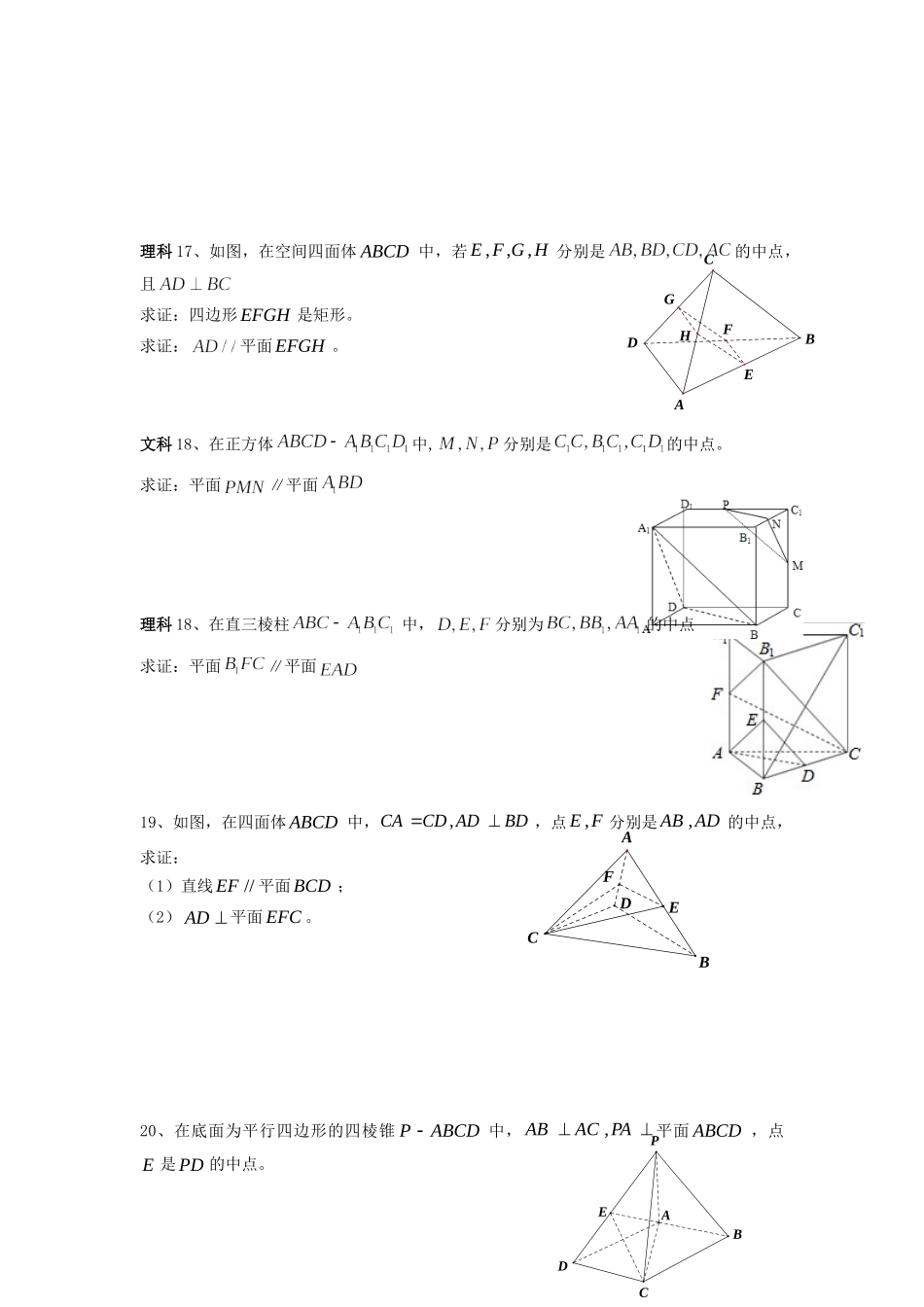
四川省攀枝花市2016-2017学年高二数学下学期第一次月考(3月调研检测)试题(无答案)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、如下图1中的几何体是由下面哪个三角形绕直线旋转所得到的:2、已知两条相交直线a、b,a∥平面α,则b与α的位置关系()A.b∥αB.b与α相交C.b⊂αD.b∥α或b与α相交3、左边是一个几何体的三视图,则这个几何体是().A.四棱锥B.圆锥C.三棱锥D.三棱台4、正方体的表面积是64,则正方体的体对角线的长为()A.34B.43C.24D.165、设m,n是两条不同的直线,α,β是两个不同的平面()A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β6、正方体A1B1C1D1-ABCD中,BD与B1C所成的角是()A.90°B.60°C.45°D.30°7、长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是().A.B.C.D.都不对8、一个空间几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.9、如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱BC、C1D1的中点,则EF与平面BB1D1D的位置关系是()A.EF∥平面BB1D1DB.EF与平面BB1D1D相交C.EF⊂平面BB1D1DD.EF与平面BB1D1D的位置关系无法判断DBACGHFE10、在正四棱锥V-ABCD中,底面正方形ABCD的边长为1,侧棱长为2,则异面直线VA与BD所成角的大小为()A.B.C.D.11、正三棱柱中,是的中点,等于,则顶点到平面的距离为().A.B.1C.D.12、如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下面命题正确的是()A.平面ADC⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ABD⊥平面ABC二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13、若正三棱柱的所有棱长均为,且其体积为,则=14、若母线长是的圆锥的轴截面的面积是4,则此圆锥的高是15、一个三角形的直观图是腰长为,底为4的等腰三角形,则原三角形面积是16、正四棱锥的底面边长为2,侧棱长均为,其正视图(主视图)和侧视图(左视图)是全等的等腰三角形,则正视图的周长为_______三、解答题(本大题共6小题,共70分,解答时应写出必要的文字说明,证明过程或演算步骤)文科17、如图,在空间四面体ABCD中,若HGFE,,,分别是的中点,求证:四边形EFGH是平行四边形。求证://BC平面EFGH。DBACGHFECBDAFEDABCPE理科17、如图,在空间四面体ABCD中,若HGFE,,,分别是的中点,且求证:四边形EFGH是矩形。求证:平面EFGH。文科18、在正方体中,分别是的中点。求证:平面∥平面理科18、在直三棱柱中,分别为的中点求证:平面∥平面19、如图,在四面体ABCD中,BDADCDCA,,点FE,分别是ADAB,的中点,求证:(1)直线//EF平面BCD;(2)AD平面EFC。20、在底面为平行四边形的四棱锥ABCDP中,PAACAB,平面ABCD,点E是PD的中点。BDCAOBDCAO(1)求证:PBAC;(2)求证://PB平面AEC。文科21、设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,1,2ACBCCD,求(1)AC与平面BCD所成角的大小;(2)异面直线AB和CD的大小.理科21、设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,1,2ACBCCD,求(1)AC与平面BCD所成角的大小;(2)二面角ABCD的大小;22、如图,点是以为直径的圆上一点,直角梯形所在平面与圆所在平面垂直,且,,,(1)证明:平面;(2)证明:平面⊥平面;(3)求三棱锥的体积.