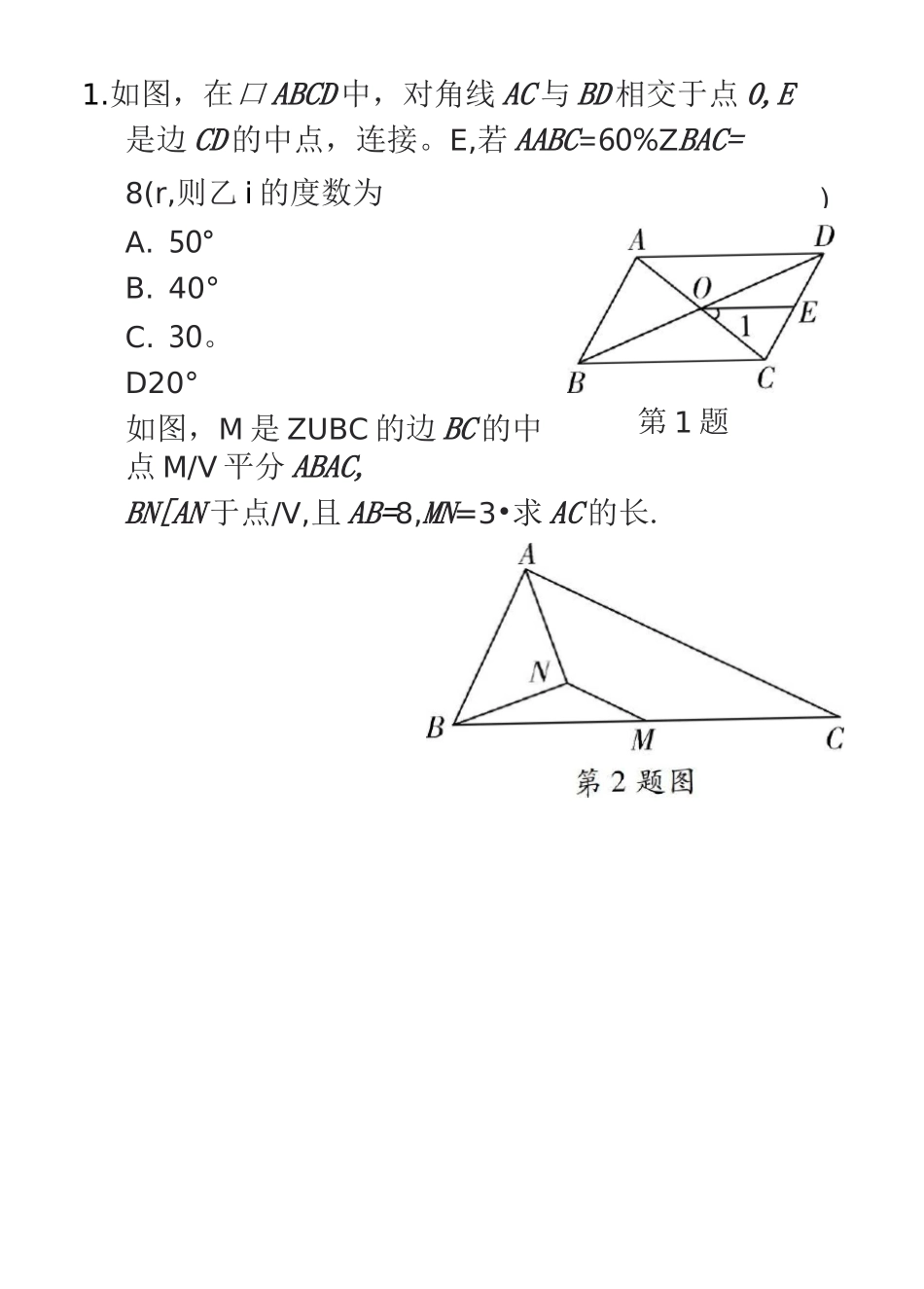
初中几何“中点问题”七大模型模型一多个中点出现或平行+中点(中点在平行线上)时,常考虑或构造三角形中位线1模型分析I在三角形中.如果有中点•可构造三角形的中位线,利用三角形中位线的性质定理:DE〃月C,且DE=解决线段之间的相等或比例关系及平行问题.AA连接^BCBC练一练1.如图,在口ABCD中,对角线AC与BD相交于点0,E是边CD的中点,连接。E,若AABC=60%ZBAC=8(r,则乙i的度数为A.50°B.40°C.30。D20°如图,M是ZUBC的边BC的中点M/V平分ABAC,BN[AN于点/V,且AB=8,MN=3•求AC的长.)第1题MDQP0BCN第3题3—如图,在四边形佃CD中,AB二分别是AD、RC、BD、AC的屮求证:胚N与PQ互相垂白平分A答案:BCN第3题解二MP//NQ且MPA四边形MRVQ是平行四边形,又丁点pJV分别是线段BD.BC的中点,/.PV是的中位线,tB2.AC-14.3.证明:如解图,顺次连接MP、PNNQ、QM,v点分别是线段仞洌的中点,是/MP//AB且二~^~AB同理.NQ//ABnNQ=~^ABNQ、:,PN二亏CD.乂丁AB二CD、/.PN二卩M,二平行四边形是菱形MN与PQ互相垂直平分.WLD模型二I直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半1模型分析I直角三角形中有斜边中点时,常作斜边上的中线,利用“斜边上的中线等于斜边的一半”可得CD=AD=BD^^-AB来解题,有时有直角无中点,要找中点,可简记为“直角+中点,等腰必呈现”.此模型作用:①证明线段相等或求线段长;②构造角相等进行等量代换.AA练一练答案:4.如图,厶4CB二90。0为AE的中点,连接DC并延长到使CE=*CD,过点B作BF//DE,与AE的延长线交于点F,若BF=8.求MB的长度・第4题图5.如图,四边形ABCD中,乙C二90。/。丄点E为的屮点,DE//BC.求证:平分乙ABC.4.AB—6-5.证明:丁皿丄帥,点E为加?的屮点...DE=BE=^-AB,/.A.ABD二LBDE.•/DE//BC,乙CED二ABDE,AABD=LCBD,:.劝平分乙MC.模型三丨等腰三角形中遇到底边上的中点,常联想“三线合一”的性质1模型分析I等腰三角形中有底边上的中点时,常作底边的中线,利用等腰三角形底边中线、高线、顶角平分线“三线合一"的性质得到:ABAD=ACAD,AD丄BC.BD=CD,解决线段相等及平行问题、角度之间的相等问题.练一练6.如图仏ABC中”点D是EC的中点,E是ACt―点,且AE=AD,若Z.AED=75求:乙劭C的度数第6题图7.如图,在△ABC中,4〃二4C二5,BC二为BC的中点』力V丄4C于点N.求MN的长.第7题图DAEB第8题图&如图,在矩形MC”中』为M边上一点』C平分ADEB.F为CE的中点,连接AF.BF.(1)求证J)E=DC;(2)求证MF丄石答案:68BFAEPC=1512MN二¥■・EF亡EC,二^_ABF-£.CEB7■/乙DCE二ZCEH,二AABF=厶DCF,在厶ABF和厶DCF中,rBF^CFJ乙AHF二厶DCF、lAB二DC/.AABF^ADCF(SAS)二厶AFB=ADFC=90\AF丄BF.DAEB第8题解图证明:(l)V四边形佔仞是矩形,二AB//CD./LDCE=ACEB,丁EC平分乙DEE,/_DEC—ACEB,/.厶DCE二厶DEC,二DE=DC;(2)如解图,连接D化vDE=DC.F为EE的中点,/.DE丄EC,二ZOFC=90%在矩形J\BCD中,AB二DC、厶模型四I遇到三角形一边垂线过这边中点时,可以考虑用垂直平分线的性质1模型分析I当三角形一边垂线过这边中点时,可以考虑用垂直平分线的性质得到:BE=CE,证明线段间的数量关系-AE连接理/〉EL1\!/1\BDCBDC/EGBDC第10题图答案:10*如图,△八BC中,AD是咼,CE是中线,点G是CE中点刀G丄CE点G为垂足.求证:DC二模型五BDC第10题解图DC二BE.v“ABC屮.AD是高,CE是屮线,二DE是RlAADB的斜边AB上的中线,10.证明:如解图,连接DE,•••G是CE的中点,DG丄CE,二DG是CE的垂直平分线,9.AABE的周长为1(1中线等分三角形面积DE二BEGEADEDC12.如图,在边长为。的正方形ABCD中工是的中点,DE交AC于点F,则ACDF的面积为()1?1.12少A”—-a"B.—-a'C.—-aD.—432316,则S1模型分析1(1)圆心()是直径的中点,常与已知中点连接,或过点。作一边的平行线或垂直构造中位线解题;(2)圆中遇到弦的中点,联想“垂径定理”,出现“四中点一垂直竹解决相应问题;(3)圆中遇到弧的中点,利用一等四等心垂径定理”解决相应问题.练一练答案:模型六I圆中弦(或弧)的中点,考虑垂径定理及圆周角定理(点&是弦的中点)(点C是AE的中点)构造全等三角形14•如图用B是半圆0的直径,AABC的两边AC.BC分别交半圆于D,E,且E为BC的中点,已知ABAC=50...