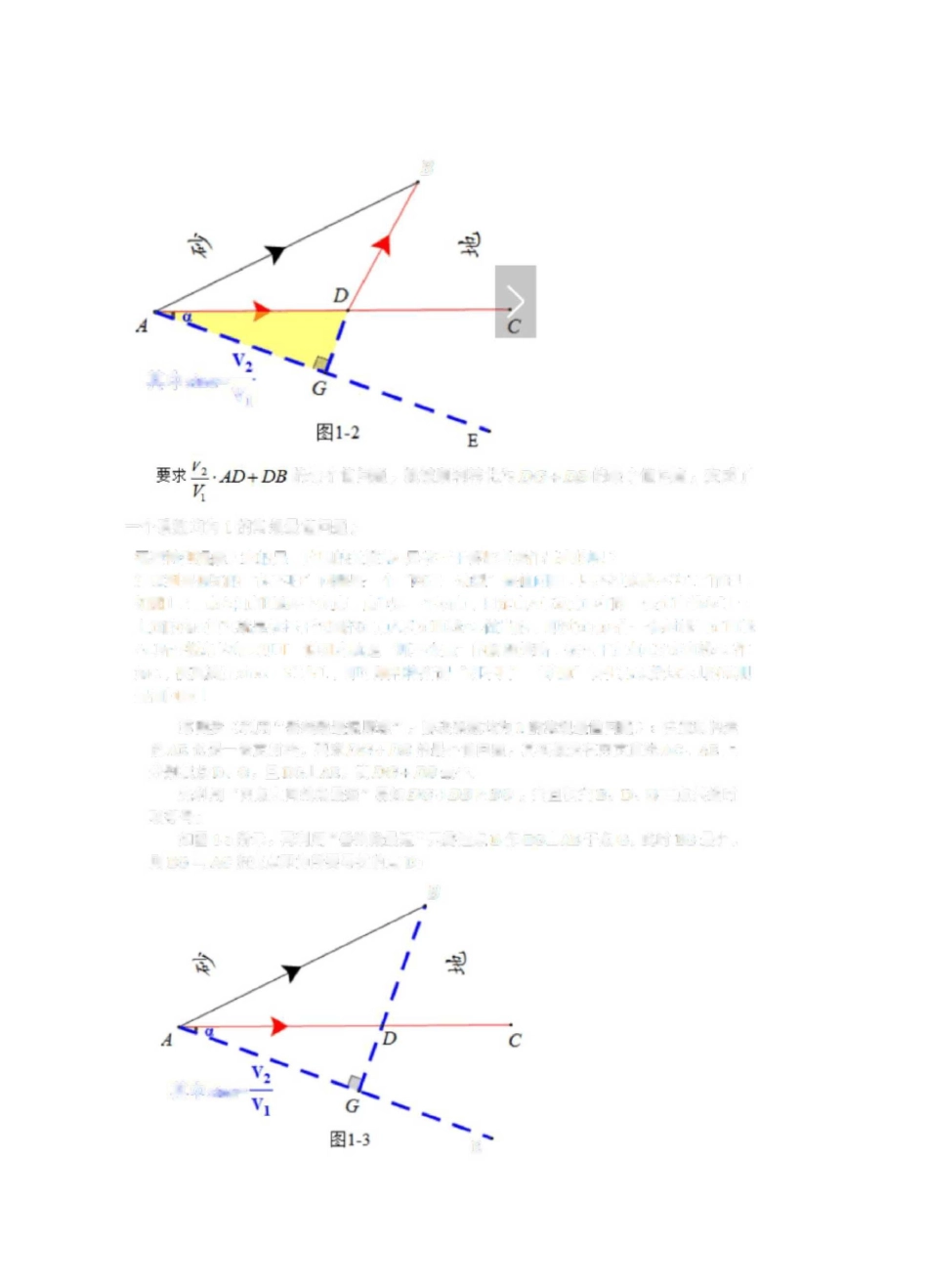
胡不归问题模型及其应用EJJ图】E1-1原題重现:(来源:高邮市聲比学融立绦习(6))如圉1所示r抛物线尸汕芥2x-m与X轴交于久E两点f过百的■袋交删绞于ErHtanzEBA=4/3.有一只蚂蚁从A出发,先以1单位/啲速度爬到线段旺上的点D处,再以1.25单位/£的逋度沿看DE爬到E点处更食”则鉛蚁从A到E的最短时闾是s.要幄解决这个所谓"琏懸“「不得不提起一起著容的、大名幄鼎的、古老的"胡不归"问题.一、模型腿故("胡不归"问题)『下文来源于网第育一则石老的历史故事:说的星一个身在他乡的<J啾子「得知父亲病危的洎宦后便日夜赶路回家撚而』当他气Q福吁吁地来到父亲的面前时,老人剛刚咽气了•人们吉诉他,在弥留之际,老人在不断嗔闻地叨念:"胡不口?胡不归?……“旦期的科学家冒为这则古老1亏说中的小快子设想了一条路琏:如圄1J所示,A星出发地,B是目的地;AC星F驿道「而驿道靠目的地的一侧全是砂土地希•为了恳切回家「小快子选扌睪了直线路程AB•但是「他葱略了在驿直上行走要比在砂土地带行走快的这一因素•如果他育绻擇一条合适的路线(尽管这条路墟长一些,但是速度却可以加快)」是可以提前抵达家门的,那么,他应该渤睪那条路线呢?显然,根据两种路面的状况和在直上行走的速度價.可以在A匚上选定一点D川秋子从A走到Dr然后从D折往Br可望星早到达目的地B.用现代的数学语言表达出釆就是:已知在驿道和砂地上行走的速廈分剧为V丄和V2,在A匚上找一定点D,使从A至D、冉从D至B的行耒时间最短.于星■■问題在于如何去找出D点遠个古老的“胡不归"问题风靡了一千多年r一育到十七世纪中叶,才由法国著窖科学家罄尔马揭幵了它的面纱.从而问題桢转化为单亍系数不为1的最值问題;二*模型脾决第一步(设出时何t,将Si学问題宇耳化):设氓吋间为口则r=—,这里X》兀婪求的就是i的最小值,逑圧一个系數不为1的最值问理,而且有两个系数均不为1;第二步{提取“大系数冷>化対只有一个系魏不対1的最値问題}:—股情妃下.谓到两个系数不为I的最值问題,首先要野其转化为里个系数不为1的最值问题,这个鹑化还圧比较奸实现的,只需提取一个系数出采即可;问題是,该提取哪个系融比镀好呢?一骰情况下,提取数值比较犬的那个系路H莹本例来说,由兀知t的柬达式中两个系因而应该提取丄出来,即声+(》.的・£>甘),注意这里片与理均为常数,这样要求t的最*佰,只要求第三步(枸造三角酌数,化为系数均为I的常規最值冋題〉的最小值冋霸呢?还是要想办法牡理不为1的系数,将系埶都化为1.但是问题来了,此时明显不能再用提取系数的办法了!那咋办?数学是门神奇的科学,只有休恒不到,没有她散不到的!联想到初中阶殿学到的锐角三角函数,可以拘谴一个直甬三角形,将不为1的系数无形中化対1,这也是解决所谓“胡不归"问瓯的核心与难点所在,具体按低如下:由令<1麻想到三角函数値,如團口所示「过定点A在直线AC的下方构适锐角ZJ7DGJ7再过动点D作DG丄AE于点G,则也=于応,从而有心彳•如BBE其中血g的最湎顶就被嗣陽MS的最小值强变成了—个系数均为1的常觌最值问題;斋要特别提醒大家的是「这里的关键甬◎是依托于哪些考虑作出来的呢?注意到最原始的"胡不归"问题星Y%宦一动雪晶借问題”只不过垂数不为1了而已:如图1-2「点A和点£是两个定点「点DJ皐一个动点.•且罡点A与动点D在同一条宦直线A匚上;上面的角空实就是依托于这里的宦点A及走直缺C做出的f即过走点A作一条肘线与圭直线AC■所交税角为角c(即可!说到底就是"抓不变量"的解题策畴,依托于定点戌及定直姪AC■作甫or使翼满足引g=V2/V1.即可顺利将肝:■“胡不归“嚨题“转化为系数均为1的窜规最值问题!第四步(利用"垂线段罠矩原理"”齡块系對均为】的常规最值问題》:注竜到构造的冉E也是一条定射纟乳要求DG+DB的最小值冋題,直实就是在两定直线扎GAE±分別找点6G>旦DG丄A£,使QG亠。迟最趴先利用“两点之间线段最短"易舸QG+DE2迟G、当怛汉当生D、G三点共线吋较茅号』如團1月所示,再利用'■■垂线段競短"只需过点B作EG丄AE于点G,此吋BG是小#则BG与AC的交点即为所费寻找的亘Dj其中sina=—*ABZQ劝癥故所求吋鯛計值哙⑷皿吨至此,”胡不归"模型得到完笑解尿!如...