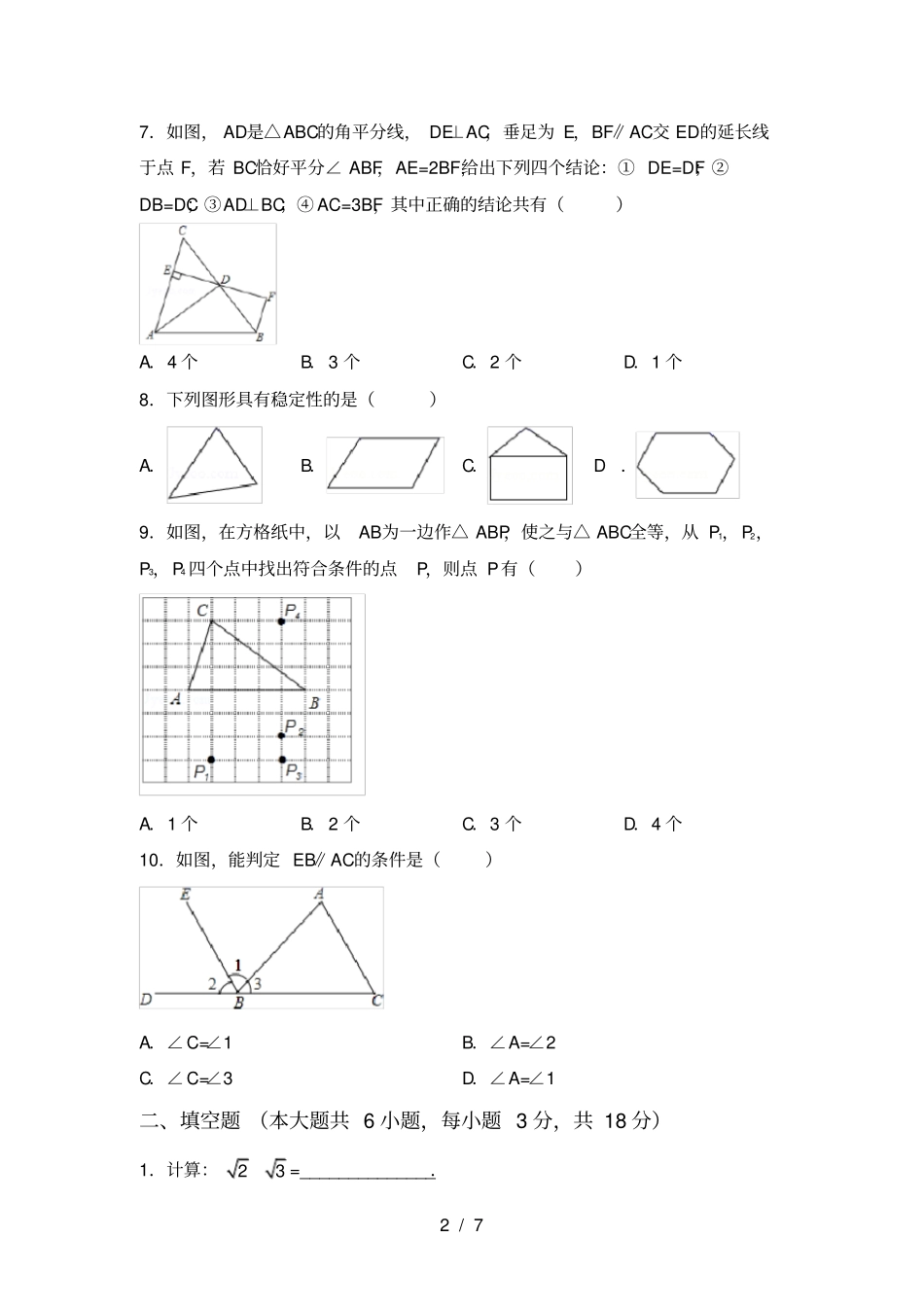
1/7人教版九年级上册数学《月考》考试题(完美版)班级:姓名:一、选择题(本大题共10小题,每题3分,共30分)1.﹣8的相反数是()A.8B.18C.18D.-82.对某市某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),绘制成如图所示统计图.已知选择鲳鱼的有40人,那么选择黄鱼的有()A.20人B.40人C.60人D.80人3.对于任意的x值都有227221xMNxxxx,则M,N值为()A.M=1,N=3B.M=﹣1,N=3C.M=2,N=4D.M=1,N=44.对于反比例函数2yx,下列说法不正确的是()A.图象分布在第二、四象限B.当0x时,y随x的增大而增大C.图象经过点(1,-2)D.若点11,Axy,22,Bxy都在图象上,且12xx,则12yy5.菱形不具备的性质是()A.四条边都相等B.对角线一定相等C.是轴对称图形D.是中心对称图形6.若3x>﹣3y,则下列不等式中一定成立的是()A.0xyB.0xyC.0xyD.0xy2/77.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A.4个B.3个C.2个D.1个8.下列图形具有稳定性的是()A.B.C.D.9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有()A.1个B.2个C.3个D.4个10.如图,能判定EB∥AC的条件是()A.∠C=∠1B.∠A=∠2C.∠C=∠3D.∠A=∠1二、填空题(本大题共6小题,每小题3分,共18分)1.计算:23=______________.3/72.因式分解:39aa_______.3.已知抛物线21yxx与x轴的一个交点为(0)m,,则代数式m2-m+2019的值为__________.4.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是__________.5.如图,直线l为y=3x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;⋯⋯,按此作法进行下去,则点An的坐标为__________.6.在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数kyx(k是常数,k≠0)的图象经过点M,交AC于点N,则MN的长度是__________.三、解答题(本大题共6小题,共72分)1.解分式方程:3213xxx4/72.关于x的一元二次方程2223()0mxmxm-有两个不相等的实数根.(1)求m的取值范围;(2)当m取满足条件的最大整数时,求方程的根.3.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.(1)当t为何值时,四边形ABQP是矩形;(2)当t为何值时,四边形AQCP是菱形;(3)分别求出(2)中菱形AQCP的周长和面积.4.在平面直角坐标系中,直线1y22x与x轴交于点B,与y轴交于点C,二次函数21ybx2xc的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.(1)求二次函数的表达式;(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.5/775迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:(1)将图1补充完整;(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是;(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.61.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售6/7单价每降低1元,每天就可多售出5...